0.037 Repeating As A Fraction
horsecheck
Sep 23, 2025 · 5 min read
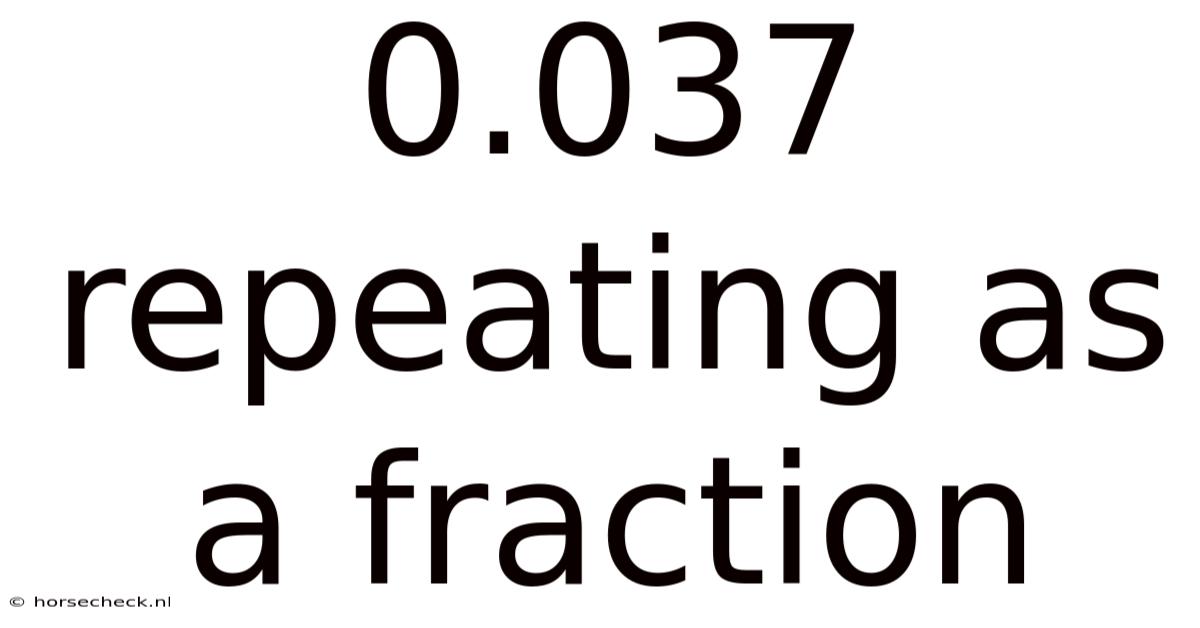
Table of Contents
Decoding the Mystery: 0.037 Repeating as a Fraction
Understanding how to convert repeating decimals, like 0.037 repeating, into fractions can seem daunting at first. But with a systematic approach and a little bit of algebra, it becomes a manageable and even fascinating process. This article will guide you through the steps, explaining the underlying mathematical principles and offering a deeper understanding of decimal-to-fraction conversion. We'll cover the process step-by-step, explore the mathematical reasoning behind it, and address frequently asked questions. By the end, you'll not only know the fractional equivalent of 0.037 repeating but also be equipped to tackle similar problems with confidence.
Understanding Repeating Decimals
Before diving into the conversion process, let's clarify what a repeating decimal is. A repeating decimal is a decimal number that has a digit or a sequence of digits that repeat infinitely. This repeating part is often indicated by a bar placed above the repeating sequence. For example, 0.333... is written as 0.$\bar{3}$, and 0.123123123... is written as 0.$\bar{123}$. In our case, we're dealing with 0.037 repeating, which can be written as 0.$\bar{037}$. This means the sequence "037" repeats endlessly.
Converting 0.037 Repeating to a Fraction: A Step-by-Step Guide
The method we'll use to convert 0.$\bar{037}$ into a fraction involves algebra. Here's a detailed breakdown:
Step 1: Assign a Variable
Let's represent the repeating decimal with a variable, say 'x'.
x = 0.$\bar{037}$
Step 2: Multiply to Shift the Decimal
We need to manipulate the equation to isolate the repeating part. The repeating block has three digits, so we'll multiply both sides of the equation by 1000 (10 raised to the power of the number of digits in the repeating block):
1000x = 37.$\bar{037}$
Step 3: Subtract the Original Equation
Now, subtract the original equation (x = 0.$\bar{037}$) from the equation we obtained in Step 2:
1000x - x = 37.$\bar{037}$ - 0.$\bar{037}$
This step elegantly eliminates the repeating decimal part:
999x = 37
Step 4: Solve for x
Now, we can solve for 'x' by dividing both sides of the equation by 999:
x = 37/999
Step 5: Simplify the Fraction (If Possible)
In this case, we need to check if the fraction can be simplified. We look for common factors between the numerator (37) and the denominator (999). Since 37 is a prime number and it does not divide 999, the fraction is already in its simplest form.
Therefore, the fractional representation of 0.$\bar{037}$ is 37/999.
The Mathematical Rationale
The method outlined above relies on the concept of representing infinite repeating decimals as geometric series. When we multiply the repeating decimal by a power of 10, we essentially shift the decimal point to the right. Subtracting the original equation cancels out the repeating part, leaving us with a simple algebraic equation to solve. The process is a clever application of manipulating infinite series to obtain a finite solution.
Further Exploration: Variations and Extensions
The method demonstrated above can be applied to any repeating decimal, regardless of the length of the repeating block or its position relative to the decimal point. For example, let's consider the decimal 0.1$\bar{23}$:
- Let x = 0.1$\bar{23}$
- Multiply by 10 to isolate the repeating part: 10x = 1.$\bar{23}$
- Multiply by 1000 to further shift the decimal: 1000x = 123.$\bar{23}$
- Subtract the equation from step 2 from step 3: 1000x - 10x = 123.$\bar{23}$ - 1.$\bar{23}$ => 990x = 122
- Solve for x: x = 122/990 = 61/495
This example shows the adaptability of the method. The key is to multiply by the appropriate power of 10 to align the repeating blocks for subtraction.
Frequently Asked Questions (FAQ)
Q1: What if the repeating decimal starts after a non-repeating part?
For example, let's consider 0.12$\bar{3}$. You'd handle the non-repeating part separately.
- Let x = 0.12$\bar{3}$
- Multiply by 100: 100x = 12.$\bar{3}$
- Multiply by 1000: 1000x = 123.$\bar{3}$
- Subtract: 1000x - 100x = 900x = 111
- Solve: x = 111/900 = 37/300
Q2: Can all repeating decimals be converted into fractions?
Yes! Every repeating decimal has a rational equivalent – a fraction where both the numerator and denominator are integers. This is a fundamental property of rational numbers.
Q3: Is there a shortcut for converting simple repeating decimals?
For decimals with a single repeating digit, like 0.$\bar{3}$, a simple shortcut exists. The fraction is the repeating digit over 9 (e.g., 0.$\bar{3}$ = 3/9 = 1/3). For two repeating digits, it's the repeating digits over 99, and so on. However, this shortcut is limited and the general algebraic method is more versatile.
Conclusion: Mastering Decimal-to-Fraction Conversions
Converting repeating decimals to fractions might seem challenging initially, but with a structured approach using algebra, it becomes a straightforward process. The key lies in strategically multiplying the equation to align the repeating blocks and then subtracting to eliminate the infinitely repeating part. This article has not only provided the solution for 0.$\bar{037}$ (which is 37/999) but also equipped you with the understanding and tools to confidently tackle any repeating decimal conversion. Remember to always simplify your fraction to its lowest terms for a complete and accurate answer. This skill is crucial not just for mathematical fluency but also for deeper understanding of number systems and their interrelationships.
Latest Posts
Latest Posts
-
Is 207 A Prime Number
Sep 24, 2025
-
What Is A 12 20
Sep 24, 2025
-
Square Root Of 162 Simplified
Sep 24, 2025
-
108 Grados Fahrenheit A Celsius
Sep 24, 2025
-
3 5 Is What Percent
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 0.037 Repeating As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.