1 1000 As A Decimal
horsecheck
Sep 24, 2025 · 5 min read
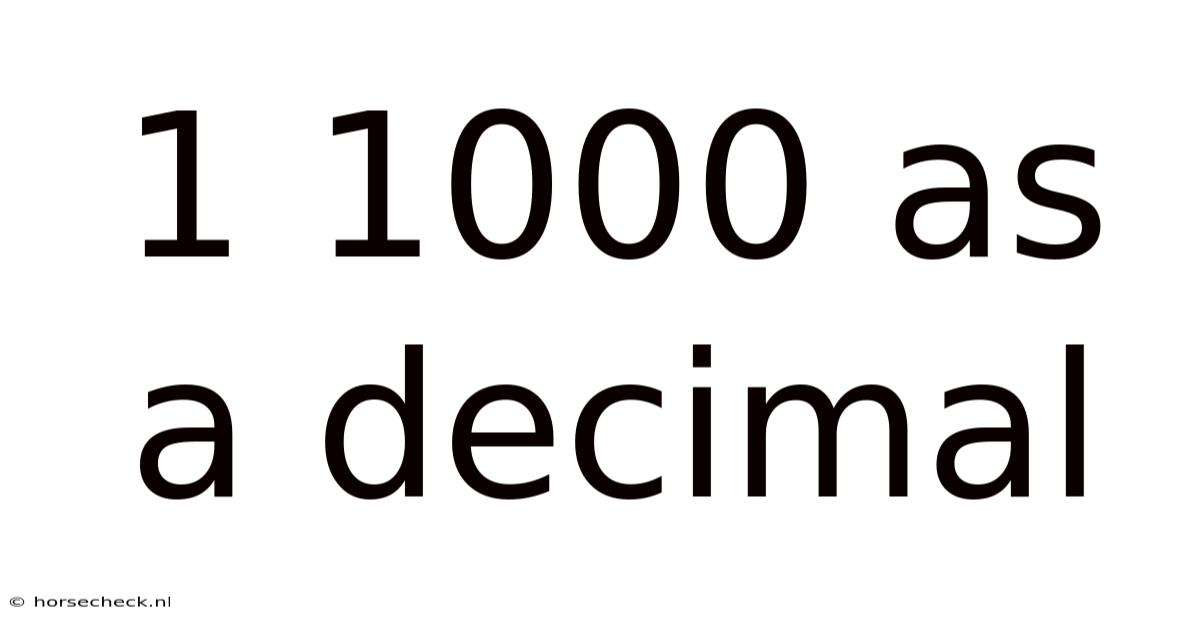
Table of Contents
Understanding 1/1000 as a Decimal: A Comprehensive Guide
The seemingly simple fraction 1/1000 might appear straightforward, but understanding its decimal equivalent and the broader concepts behind it unlocks a deeper understanding of decimal representation and its applications in various fields like science, finance, and engineering. This article will provide a comprehensive guide to understanding 1/1000 as a decimal, exploring its conversion process, practical applications, and addressing frequently asked questions.
Introduction: Decimals and Fractions
Before diving into the specifics of 1/1000, let's establish a foundational understanding of decimals and fractions. A fraction represents a part of a whole, expressed as a ratio of two numbers (numerator and denominator). A decimal, on the other hand, represents a fraction where the denominator is a power of 10 (10, 100, 1000, and so on). Decimals are a convenient way to represent fractional values, particularly when dealing with calculations and measurements.
Converting 1/1000 to a Decimal
Converting a fraction to a decimal is a relatively straightforward process. The simplest approach is to perform the division indicated by the fraction: divide the numerator (1) by the denominator (1000).
1 ÷ 1000 = 0.001
Therefore, 1/1000 expressed as a decimal is 0.001.
Understanding Place Value in Decimals
To fully grasp the meaning of 0.001, it's essential to understand decimal place value. Each digit in a decimal number holds a specific value depending on its position relative to the decimal point.
- The first digit to the right of the decimal point represents tenths (1/10).
- The second digit represents hundredths (1/100).
- The third digit represents thousandths (1/1000).
- And so on...
In the decimal 0.001, the digit '1' is in the thousandths place, indicating one-thousandth (1/1000). The zeros act as placeholders, signifying the absence of any value in the tenths and hundredths places.
Alternative Methods for Conversion
While simple division works effectively, alternative methods can provide a deeper understanding of the conversion process. One such method involves expanding the fraction to have a denominator that is a power of 10. Since 1/1000 already has a denominator that is a power of 10, no further manipulation is needed. However, if we were dealing with a fraction like 1/4, we would need to find an equivalent fraction with a denominator of 10, 100, 1000, etc. In this case, 1/4 can be converted to 25/100, which is equal to 0.25.
Practical Applications of 1/1000 (0.001)
The decimal 0.001, or one-thousandth, appears in numerous practical applications across various fields:
-
Science and Engineering: In scientific measurements, 0.001 represents a milli-unit. For example, 1 milliliter (mL) is equal to 0.001 liters (L), 1 millimeter (mm) is 0.001 meters (m), and 1 milligram (mg) is 0.001 grams (g). This unit is crucial for precise measurements in various scientific experiments and engineering designs.
-
Finance: In financial calculations, 0.001 can represent a basis point (bps). A basis point is one-hundredth of a percentage point, often used to describe small changes in interest rates or yields. A change of 10 basis points, for example, represents a change of 0.1%.
-
Computing: In computer science, particularly in relation to floating-point numbers, understanding thousandths is essential for handling fractional values. Many algorithms and computations rely on precise decimal representations, with 0.001 serving as a fundamental unit in various calculations.
-
Manufacturing and Precision Engineering: In industries demanding high precision, such as manufacturing of microchips or precision instruments, tolerances are often expressed in thousandths of an inch or millimeters. 0.001 represents a crucial level of accuracy in these processes.
Scientific Notation and 1/1000
For very small or very large numbers, scientific notation provides a more concise and manageable representation. In scientific notation, 0.001 is expressed as 1 x 10⁻³. The exponent (-3) indicates that the decimal point should be moved three places to the left.
Understanding Percentages and 1/1000
To express 1/1000 as a percentage, we multiply the decimal equivalent (0.001) by 100%:
0.001 x 100% = 0.1%
Therefore, 1/1000 is equal to 0.1%. This represents one-tenth of one percent.
Comparison with other Fractions
Comparing 1/1000 to other common fractions helps contextualize its magnitude.
- 1/1000 is smaller than 1/100 (0.01)
- 1/1000 is smaller than 1/10 (0.1)
- 1/1000 is much smaller than 1/2 (0.5) or 1/4 (0.25)
This comparison highlights the relatively small magnitude of 1/1000.
Working with 1/1000 in Calculations
Performing calculations involving 1/1000 (0.001) is similar to working with other decimals. For example:
- Adding: 2.5 + 0.001 = 2.501
- Subtracting: 5.2 - 0.001 = 5.199
- Multiplying: 10 x 0.001 = 0.01
- Dividing: 0.5 ÷ 0.001 = 500
These examples demonstrate the ease of incorporating 1/1000 into various calculations.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between 1/1000 and 0.001?
- A: There is no difference. 1/1000 and 0.001 are simply two different representations of the same value.
-
Q: How do I convert other fractions to decimals?
- A: To convert any fraction to a decimal, divide the numerator by the denominator.
-
Q: What is the significance of the zeros in 0.001?
- A: The zeros are placeholders that indicate the absence of values in the tenths and hundredths places. They are crucial for maintaining the correct place value of the digit '1' in the thousandths place.
-
Q: Are there any limitations to representing 1/1000 as a decimal?
- A: While decimal representation is generally precise, some fractions cannot be represented exactly as finite decimals (e.g., 1/3). However, 1/1000 can be represented exactly as 0.001.
Conclusion: Mastering 1/1000 as a Decimal
Understanding 1/1000 as a decimal (0.001) is not only crucial for basic arithmetic but also essential for comprehending more complex concepts in various fields. By understanding decimal place value, conversion methods, and practical applications, one gains a firmer grasp of numerical representation and its importance in quantitative analysis. The seemingly simple fraction 1/1000 opens doors to a wider world of mathematical understanding and its real-world implications. This knowledge serves as a building block for more advanced mathematical concepts and problem-solving abilities. From scientific measurements to financial calculations, the ability to confidently work with 1/1000 and its decimal equivalent significantly enhances one's analytical skills and practical capabilities.
Latest Posts
Latest Posts
-
71 Grad Fahrenheit In Celsius
Sep 24, 2025
-
What Is A 30 35 Grade
Sep 24, 2025
-
List The Factors Of 18
Sep 24, 2025
-
What Is 35 Degrees C
Sep 24, 2025
-
Gcf Of 15 And 27
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 1 1000 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.