1/3 Is How Much Percentage
horsecheck
Sep 23, 2025 · 5 min read
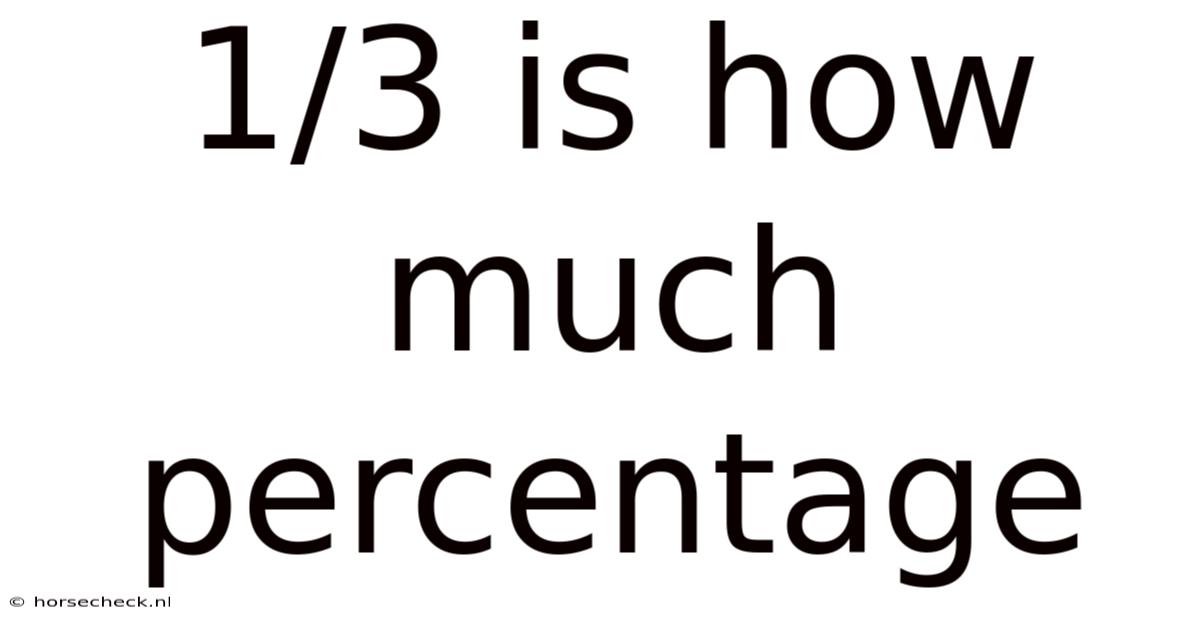
Table of Contents
1/3 is How Much Percentage? Understanding Fractions and Percentages
Understanding the relationship between fractions and percentages is a fundamental skill in mathematics, crucial for everyday life, from calculating discounts to understanding financial reports. This article will delve deep into the conversion of fractions to percentages, focusing specifically on how to determine what percentage 1/3 represents. We'll explore the process step-by-step, providing clear explanations and examples, and even tackling some common misconceptions. By the end, you'll not only know the answer but also grasp the underlying principles, empowering you to tackle similar conversions confidently.
Introduction: Fractions, Decimals, and Percentages - A Trifecta
Before diving into the specific conversion of 1/3, let's establish a clear understanding of the relationship between fractions, decimals, and percentages. These three represent different ways of expressing parts of a whole.
-
Fractions: Fractions represent parts of a whole using a numerator (top number) and a denominator (bottom number). For example, 1/3 means one part out of three equal parts.
-
Decimals: Decimals represent parts of a whole using base-ten notation. They use a decimal point to separate the whole number from the fractional part. For instance, 0.5 represents one-half.
-
Percentages: Percentages represent parts of a whole as a fraction of 100. The symbol "%" represents "per hundred." For example, 50% means 50 out of 100, or one-half.
The beauty of these three systems is their interchangeability. You can easily convert between them, which is precisely what we'll be doing with 1/3.
Converting 1/3 to a Percentage: A Step-by-Step Guide
Converting a fraction to a percentage involves two primary steps:
Step 1: Convert the Fraction to a Decimal
To convert a fraction to a decimal, we divide the numerator by the denominator. In the case of 1/3:
1 ÷ 3 = 0.333333...
Notice the repeating decimal. This is characteristic of some fractions, and it means the decimal representation goes on infinitely. For practical purposes, we often round the decimal to a certain number of decimal places.
Step 2: Convert the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol. Using the decimal representation of 1/3 (rounded to a few decimal places for simplicity):
0.3333 x 100 = 33.33%
Therefore, 1/3 is approximately 33.33%. The three dots (...) after 33.33 indicate that it is an approximation, as the decimal representation of 1/3 continues infinitely.
Understanding the Repeating Decimal: Why 1/3 Doesn't Convert to a Neat Percentage
The repeating decimal in the conversion of 1/3 (0.3333...) is a crucial point to understand. It's not a limitation of our calculation; it's inherent to the fraction itself. Some fractions, when expressed as decimals, result in non-terminating, repeating decimals. This is because the denominator (3, in this case) has prime factors other than 2 and 5. Only fractions with denominators whose prime factors are solely 2 and 5 will result in terminating decimals.
This means that there is no exact percentage equivalent for 1/3. 33.33% is simply a rounded approximation. To express the exact value, we must either remain in fractional form (1/3) or use the repeating decimal notation (0.333...).
Real-World Applications of 1/3 and its Percentage Equivalent
The knowledge of converting 1/3 to a percentage, even with its approximate nature, has widespread applications in various real-world scenarios. Consider these examples:
-
Sales and Discounts: If a store offers a 1/3 discount, you now know that's approximately a 33.33% discount.
-
Recipe Conversions: If a recipe calls for 1/3 cup of an ingredient, and you need to double or triple the recipe, knowing the percentage equivalent aids in quick calculations.
-
Data Analysis and Statistics: In statistics and data analysis, you frequently encounter fractions that need to be expressed as percentages for easier interpretation and visualization.
-
Financial Calculations: Understanding fractions and percentages is fundamental for managing personal finances, interpreting financial statements, and understanding interest rates.
Frequently Asked Questions (FAQs)
Q: Is 33.33% the exact percentage equivalent of 1/3?
A: No. 33.33% is an approximation. The exact representation requires the use of a repeating decimal (0.333...) or the fraction itself (1/3).
Q: How can I express 1/3 as a percentage without rounding?
A: You can't express 1/3 as an exact percentage using a finite decimal. You must use the repeating decimal (33.333...)% or stick with the fraction (1/3).
Q: What if I need a more precise percentage equivalent for 1/3 in a specific calculation?
A: The level of precision needed will dictate how many decimal places you retain in your approximation. For most applications, 33.33% is sufficient; however, for highly accurate calculations, you might use more decimal places.
Advanced Concepts: Working with Repeating Decimals
Dealing with repeating decimals can be tricky, especially in more complex calculations. Here are a few points to keep in mind:
-
Using Fractions: In many instances, it's simpler and more accurate to retain fractions throughout your calculations, only converting to a percentage at the very end.
-
Symbolic Notation: In advanced mathematics, the repeating decimal is often represented using a bar over the repeating digits (e.g., 0.3̅3̅).
-
Computational Tools: Calculators and software programs can handle repeating decimals more effectively than manual calculations, offering higher precision.
Conclusion: Mastering Fractions and Percentages
Understanding the conversion between fractions and percentages is a valuable skill with widespread applications. While 1/3 doesn't have a neat percentage equivalent due to its repeating decimal nature, we can approximate it accurately as 33.33% for most practical purposes. Remember to always consider the required precision and choose the representation (fraction or approximate percentage) that best suits the context of your problem. By mastering this fundamental concept, you'll be better equipped to navigate various numerical challenges in your daily life and academic pursuits. The key takeaway is to appreciate both the approximate nature and the practical utility of converting 1/3 to its percentage equivalent. This understanding lays the groundwork for tackling more complex fractional and percentage calculations in the future.
Latest Posts
Latest Posts
-
Gcf Of 27 And 54
Sep 23, 2025
-
2 1 4 As Improper Fraction
Sep 23, 2025
-
Gcf Of 15 And 30
Sep 23, 2025
-
84 Out Of 100 Grade
Sep 23, 2025
-
46 Grados Centigrados A Farenheit
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1/3 Is How Much Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.