1 6 Equals What Percent
horsecheck
Sep 25, 2025 · 6 min read
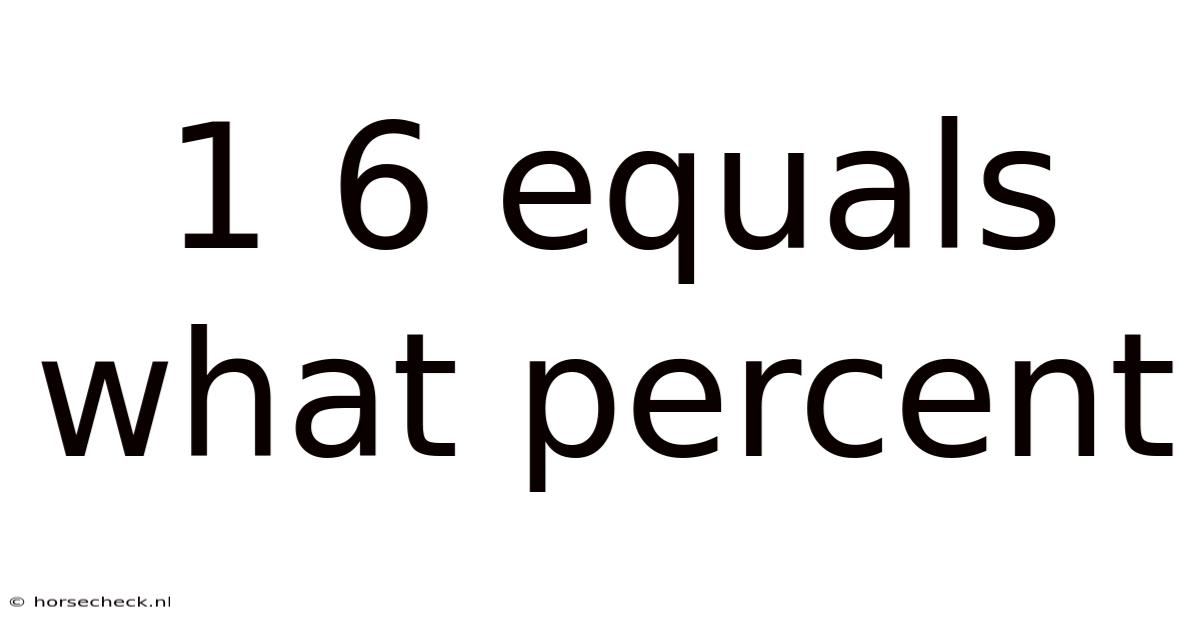
Table of Contents
1/6 Equals What Percent? Understanding Fractions, Decimals, and Percentages
Understanding the relationship between fractions, decimals, and percentages is a fundamental skill in mathematics. This comprehensive guide will delve into the process of converting the fraction 1/6 into its percentage equivalent, explaining the underlying principles and providing various approaches to solve similar problems. We'll cover not just the calculation but also the practical applications and contextual understanding of this conversion. By the end, you'll be confident in handling similar fraction-to-percentage conversions and grasping the broader mathematical concepts involved.
Understanding the Fundamentals: Fractions, Decimals, and Percentages
Before diving into the specific calculation of 1/6 as a percentage, let's establish a solid foundation.
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many parts make up the whole. For example, in the fraction 1/6, 1 is the numerator and 6 is the denominator. This means we have 1 part out of a total of 6 equal parts.
-
Decimals: Decimals represent numbers less than one using a base-ten system. They are written using a decimal point (.) to separate the whole number part from the fractional part. For instance, 0.5 represents one-half (1/2), and 0.25 represents one-quarter (1/4).
-
Percentages: Percentages represent a fraction of 100. The symbol "%" signifies "per hundred." A percentage expresses a proportion out of 100. For example, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5.
The three—fractions, decimals, and percentages—are interconnected and can be easily converted from one form to another. This interoperability is crucial for solving various mathematical problems and interpreting data.
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is a common and straightforward method. We'll first convert the fraction 1/6 into a decimal and then convert that decimal into a percentage.
-
Fraction to Decimal: To convert a fraction to a decimal, we divide the numerator by the denominator. In this case:
1 ÷ 6 = 0.166666...
Notice that this decimal is a repeating decimal, meaning the digit 6 repeats infinitely. For practical purposes, we'll round this to a suitable number of decimal places. Let's use four decimal places for now: 0.1667.
-
Decimal to Percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the percentage symbol (%).
0.1667 × 100 = 16.67%
Therefore, 1/6 is approximately equal to 16.67%. Remember that this is a rounded value; the true percentage representation of 1/6 has an infinitely repeating decimal component.
Method 2: Using Proportions
This method directly relates the fraction to the percentage by setting up a proportion. We know that a percentage is a fraction out of 100. We can set up a proportion:
1/6 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
6x = 100
x = 100 ÷ 6
x = 16.6666...
Again, we get a repeating decimal. Rounding to two decimal places, we get 16.67%.
Method 3: Understanding the Concept of "Parts of a Whole"
A more intuitive approach involves considering the fraction 1/6 in the context of a whole divided into six equal parts. If we had a pie cut into six equal slices, 1/6 would represent one slice. To find the percentage, we determine what percentage one slice represents out of the whole pie (six slices):
(1 slice / 6 slices) * 100% = 16.67%
This method helps visualize the fraction and its percentage equivalent.
Why the Repeating Decimal?
The repeating decimal in the decimal representation of 1/6 (0.1666...) arises because 6 is not a factor of 10 (or any power of 10). When converting fractions to decimals, we essentially divide the numerator by the denominator. If the denominator contains prime factors other than 2 and 5 (the prime factors of 10), the resulting decimal will be a repeating decimal. Since the prime factorization of 6 is 2 x 3, and it contains a 3, we get a repeating decimal.
Practical Applications of 1/6 as a Percentage
Understanding the percentage equivalent of 1/6 is useful in various real-world scenarios:
-
Discount Calculations: A store might offer a 1/6 discount on an item. Knowing this equates to approximately 16.67% off makes it easier to calculate the final price.
-
Data Analysis: When analyzing data presented as fractions, converting them to percentages allows for easier comparison and interpretation.
-
Probability: In probability calculations, the likelihood of an event can be expressed as a fraction, which can then be converted to a percentage for a clearer understanding.
-
Recipe Conversions: If a recipe calls for 1/6 of a cup of an ingredient, understanding its percentage equivalent might help in scaling the recipe up or down.
Frequently Asked Questions (FAQ)
-
Q: Is 16.67% the exact value of 1/6?
A: No, 16.67% is a rounded approximation. The exact value has an infinitely repeating decimal: 16.666...%
-
Q: How many decimal places should I round to?
A: The number of decimal places depends on the context. For most practical purposes, two or three decimal places (16.67% or 16.667%) are sufficient. Higher precision might be necessary in scientific or engineering applications.
-
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators have functions to perform this conversion directly. You can simply divide the numerator by the denominator and then multiply by 100.
-
Q: What if the fraction is more complex than 1/6?
A: The same principles apply. Divide the numerator by the denominator to get the decimal equivalent, and then multiply by 100 to get the percentage. The complexity arises primarily with repeating decimals, requiring rounding to a desired level of precision.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a valuable skill with wide-ranging applications. Understanding the methods outlined in this guide—using direct division, proportions, or intuitive reasoning—will empower you to tackle similar conversions with confidence. Remember that the process involves converting the fraction to a decimal and then multiplying by 100. While rounding might be necessary for practical purposes, always be mindful of the inherent precision limitations introduced by rounding repeating decimals. Practice makes perfect, so continue practicing these conversion techniques to solidify your understanding and improve your speed and accuracy. Through consistent practice and a clear understanding of the underlying principles, you'll master this essential mathematical skill.
Latest Posts
Latest Posts
-
What Percentage Is 36 40
Sep 25, 2025
-
Convert 102 Fahrenheit To Celsius
Sep 25, 2025
-
What Times What Equals 225
Sep 25, 2025
-
What Is 2 Of 21
Sep 25, 2025
-
Convert 63 Fahrenheit To Celsius
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 1 6 Equals What Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.