12 Divided By 1 1/2
horsecheck
Sep 22, 2025 · 5 min read
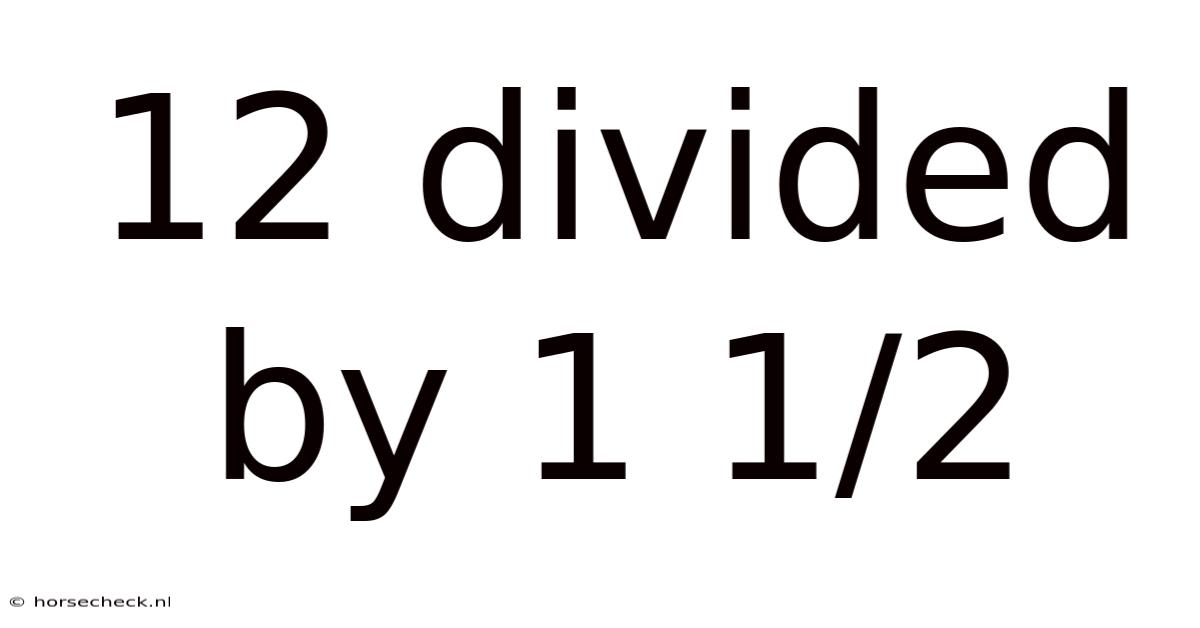
Table of Contents
12 Divided by 1 1/2: A Comprehensive Guide to Fraction Division
Dividing by fractions can seem daunting at first, but with a clear understanding of the principles involved, it becomes a straightforward process. This article will comprehensively explore how to solve 12 divided by 1 1/2, explaining the underlying mathematical concepts, providing step-by-step solutions, and addressing common questions. We will delve into different approaches, ensuring you grasp the core concepts and can apply them to similar problems with confidence. This guide aims to empower you with the skills to tackle fraction division effectively.
Understanding the Problem: 12 ÷ 1 1/2
Before diving into the solution, let's clarify the problem. We are asked to divide the whole number 12 by the mixed number 1 1/2. This means we need to determine how many times 1 1/2 fits into 12. Understanding this visual representation helps in grasping the concept before tackling the mathematical steps.
Method 1: Converting to Improper Fractions
This is a widely used method for solving division problems involving fractions. The first step involves converting both the whole number and the mixed number into improper fractions.
-
Converting 12 to an improper fraction: A whole number can be represented as a fraction by placing it over 1. Therefore, 12 becomes 12/1.
-
Converting 1 1/2 to an improper fraction: To convert a mixed number to an improper fraction, we multiply the whole number (1) by the denominator (2) and add the numerator (1). This sum (1*2 + 1 = 3) becomes the new numerator, while the denominator remains the same (2). Thus, 1 1/2 becomes 3/2.
Now, our problem becomes: (12/1) ÷ (3/2)
Method 2: Reciprocals and Multiplication
Dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction is obtained by switching the numerator and the denominator. The reciprocal of 3/2 is 2/3.
Therefore, our problem transforms into a multiplication problem: (12/1) x (2/3)
Solving the Multiplication Problem
Now we can simply multiply the numerators together and the denominators together:
(12 x 2) / (1 x 3) = 24/3
Finally, we simplify the resulting fraction by dividing the numerator (24) by the denominator (3):
24 ÷ 3 = 8
Therefore, 12 divided by 1 1/2 equals 8.
Method 3: Long Division with Fractions
While less common for this specific problem, it's useful to understand long division with fractions as a broader mathematical skill. This method involves repeatedly subtracting the divisor (1 1/2) from the dividend (12) until we reach zero.
- First Subtraction: 12 - 1 1/2 = 10 1/2
- Second Subtraction: 10 1/2 - 1 1/2 = 9
- Third Subtraction: 9 - 1 1/2 = 7 1/2
- Fourth Subtraction: 7 1/2 - 1 1/2 = 6
- Fifth Subtraction: 6 - 1 1/2 = 4 1/2
- Sixth Subtraction: 4 1/2 - 1 1/2 = 3
- Seventh Subtraction: 3 - 1 1/2 = 1 1/2
- Eighth Subtraction: 1 1/2 - 1 1/2 = 0
We subtracted 1 1/2 eight times from 12 to reach zero, confirming our answer: 8.
The Importance of Understanding Fraction Division
Mastering fraction division is crucial for various aspects of mathematics and everyday life. It forms the foundation for more advanced mathematical concepts like algebra and calculus. Furthermore, it has practical applications in fields like cooking (adjusting recipes), construction (measuring materials), and even finance (calculating proportions).
Expanding Your Knowledge: More Complex Problems
The principles discussed above can be applied to more complex problems involving fractions. For instance, consider dividing a fraction by a fraction: (2/3) ÷ (1/4). The steps remain similar: convert to improper fractions if necessary, find the reciprocal of the divisor, and then multiply.
Another scenario could involve dividing a decimal by a fraction. In such cases, convert the decimal into a fraction first and then follow the steps outlined previously.
Frequently Asked Questions (FAQ)
Q: Why do we use reciprocals when dividing fractions?
A: Dividing by a fraction is essentially asking "how many times does this fraction go into the other number?" Multiplying by the reciprocal is a mathematical shortcut that achieves the same result. It's based on the inverse relationship between multiplication and division.
Q: Can I use a calculator to solve fraction division problems?
A: Yes, most calculators have the capability to handle fractions. However, it is highly recommended to understand the underlying mathematical principles before relying solely on a calculator.
Q: What if I get a decimal answer after simplifying the fraction?
A: A decimal answer is perfectly acceptable, especially when dealing with real-world applications. For example, if you were dividing ingredients for a recipe, a decimal answer would represent a fractional part of a unit (e.g., 0.5 cups).
Q: Are there other methods to solve fraction division problems?
A: While the methods discussed are the most common and efficient, there are other approaches, particularly visual methods involving diagrams or models, that can aid in understanding the concept, especially for beginners.
Conclusion
Solving 12 divided by 1 1/2 involves a systematic approach that combines the conversion of numbers into improper fractions, the application of reciprocals, and straightforward multiplication. The answer is unequivocally 8. Understanding these steps not only provides the solution to this particular problem but also equips you with the fundamental skills to tackle a wide range of fraction division problems, paving the way for more advanced mathematical explorations. Remember, practice is key to mastering this concept – so grab some more problems and put your newfound skills to the test!
Latest Posts
Latest Posts
-
What Is 3 Of 8
Sep 22, 2025
-
50 With 40 Percent Off
Sep 22, 2025
-
All The Multiples Of 42
Sep 22, 2025
-
What Percent Is 11 30
Sep 22, 2025
-
4 2 As A Mixed Number
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 12 Divided By 1 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.