12 Out Of 20 Percentage
horsecheck
Sep 22, 2025 · 6 min read
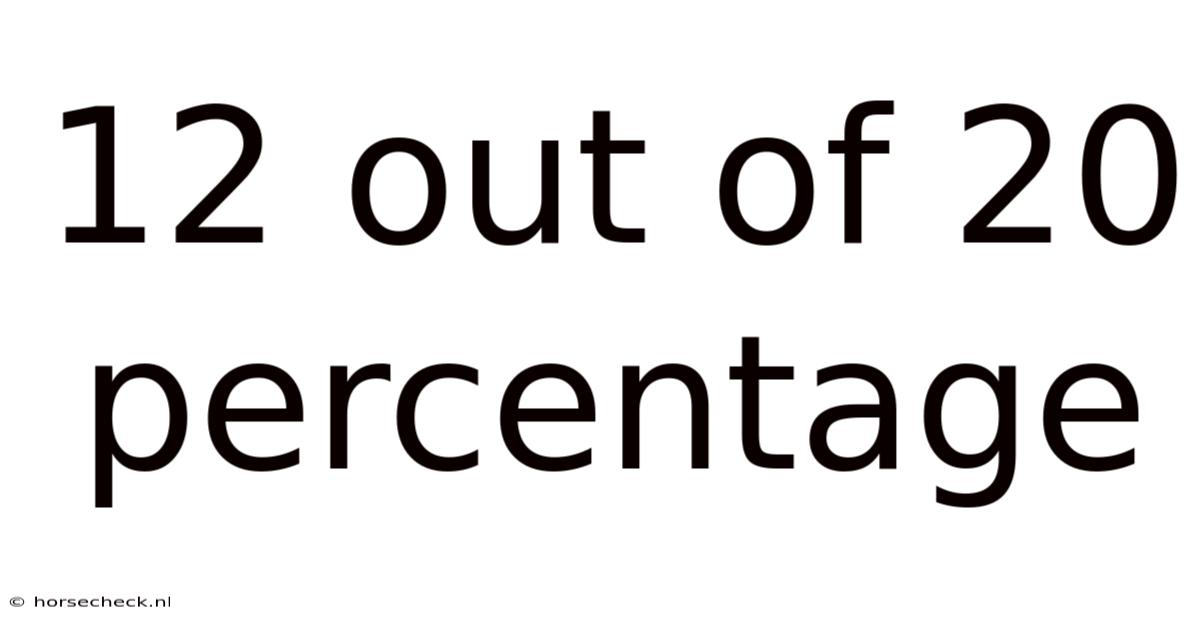
Table of Contents
Understanding 12 out of 20: Fractions, Percentages, and Their Real-World Applications
Calculating percentages is a fundamental skill applicable across numerous fields, from finance and academics to everyday life. Understanding how to convert fractions to percentages and vice versa is crucial for interpreting data, making informed decisions, and solving various problems. This article will thoroughly explore the concept of "12 out of 20," explaining its representation as a fraction, percentage, decimal, and demonstrating its practical relevance through real-world examples. We'll also delve into the broader mathematical principles behind percentage calculations.
1. Expressing 12 out of 20 as a Fraction
The phrase "12 out of 20" directly translates into the fraction 12/20. This represents 12 parts out of a total of 20 equal parts. Fractions are a fundamental way to express parts of a whole. The number on top (12) is the numerator, representing the portion we're interested in. The number on the bottom (20) is the denominator, representing the total number of parts.
This fraction can be simplified by finding the greatest common divisor (GCD) of 12 and 20, which is 4. Dividing both the numerator and the denominator by 4, we get the simplified fraction 3/5. This means that "12 out of 20" is equivalent to "3 out of 5." Both fractions represent the same proportion.
2. Converting the Fraction to a Percentage
To convert a fraction to a percentage, we need to express it as a fraction with a denominator of 100. We can do this by performing the following calculation:
(12/20) * (100/1) = 60/1 = 60%
Alternatively, we can use the simplified fraction:
(3/5) * (100/1) = 300/5 = 60%
Therefore, 12 out of 20 is equal to 60%. The percentage sign (%) signifies "per hundred" or "out of 100."
3. Representing 12 out of 20 as a Decimal
Percentages are easily converted to decimals by dividing the percentage by 100. In this case:
60% / 100 = 0.6
Therefore, 12 out of 20 is also represented as the decimal 0.6. Decimals are another way to express parts of a whole, particularly useful in calculations involving computers and calculators.
4. Real-World Applications of "12 out of 20"
Understanding how to represent "12 out of 20" in different forms has widespread applications. Consider the following examples:
-
Academic Performance: If a student answers 12 questions correctly out of 20 on a test, their score is 60%. This provides a clear indication of their performance relative to the total number of questions.
-
Sales Targets: If a salesperson aims to make 20 sales and achieves 12, they have reached 60% of their target. This helps in tracking progress and identifying areas for improvement.
-
Manufacturing Quality Control: If a factory produces 20 items, and 12 pass quality control checks, the pass rate is 60%. This metric is crucial for monitoring product quality and identifying potential production issues.
-
Survey Results: If 12 out of 20 respondents in a survey agree with a particular statement, the agreement rate is 60%. This gives valuable insight into public opinion or customer satisfaction.
-
Financial Investments: If an investment portfolio consists of 20 different stocks, and 12 are performing above the market average, this represents a 60% success rate for the investment strategy.
-
Sports Statistics: In many sports, success rates are expressed as percentages. For example, if a basketball player makes 12 out of 20 free throws, their free-throw percentage is 60%.
-
Project Completion: If a project has 20 tasks, and 12 are completed, 60% of the project is finished. This is useful for project management and reporting progress to stakeholders.
These examples highlight the importance of understanding how to interpret and utilize fractions, percentages, and decimals in various contexts. The ability to readily convert between these forms allows for easier comparison and analysis of data.
5. Further Exploring Percentage Calculations
Understanding "12 out of 20" provides a basis for exploring more complex percentage calculations. Let's examine some related concepts:
-
Calculating Percentages of Different Quantities: If you want to find 60% (the equivalent of 12 out of 20) of a different number, say 50, you would multiply 50 by 0.6 (the decimal equivalent of 60%). This gives you 30. Therefore, 60% of 50 is 30.
-
Finding the Original Quantity from a Percentage: If you know that 60% of a quantity is 30, you can find the original quantity by dividing 30 by 0.6. This gives you 50, the original quantity.
-
Percentage Increase and Decrease: Percentages are used extensively to represent increases or decreases in quantities. For instance, if a price increases from $50 to $60, the percentage increase is calculated as: [(60-50)/50] * 100% = 20%. Similarly, a decrease can be calculated.
-
Compounding Percentages: When percentages are applied repeatedly (e.g., compound interest), the calculations become slightly more complex, involving exponential functions.
6. Common Mistakes to Avoid
When working with percentages, it's crucial to avoid common mistakes:
-
Confusing Percentages and Fractions: Always ensure you correctly convert between fractions and percentages before performing any calculations.
-
Incorrect Decimal Placements: Pay close attention to decimal points when converting between decimals and percentages. A misplaced decimal can lead to significant errors.
-
Incorrect Order of Operations: When performing complex calculations involving percentages, follow the correct order of operations (PEMDAS/BODMAS) to avoid mistakes.
-
Failing to Simplify Fractions: Simplifying fractions before converting to percentages makes the calculation easier and less prone to errors.
7. Frequently Asked Questions (FAQs)
Q: What is the simplest form of the fraction representing 12 out of 20?
A: The simplest form is 3/5.
Q: How do you convert 12/20 to a percentage?
A: Divide 12 by 20 and then multiply by 100, resulting in 60%. Alternatively, simplify the fraction to 3/5 and then multiply by 100 to get 60%.
Q: What is the decimal equivalent of 60%?
A: 0.6
Q: Can you give an example of how 12 out of 20 is used in a real-world scenario?
A: In a class of 20 students, if 12 students passed a test, the pass rate is 60%.
Q: What are some common errors to watch out for when calculating percentages?
A: Misplacing decimal points, not simplifying fractions before calculation, and incorrect order of operations.
8. Conclusion
Understanding the concept of "12 out of 20" goes beyond a simple fraction. It involves grasping the interconnectedness of fractions, percentages, and decimals. This understanding forms the bedrock for more complex mathematical concepts and is invaluable for interpreting data and making informed decisions in various aspects of life. By mastering these fundamental skills, individuals can confidently navigate situations requiring percentage calculations, improving their problem-solving abilities and overall numeracy. Remember to practice regularly and focus on accuracy to solidify your understanding of these important mathematical concepts. The more you practice, the more natural and intuitive these conversions will become.
Latest Posts
Latest Posts
-
8 Qt How Many Pt
Sep 22, 2025
-
3 5 Is Equal To What
Sep 22, 2025
-
To The Power Of 6
Sep 22, 2025
-
Is 301 A Prime Number
Sep 22, 2025
-
Lcm Of 6 And 18
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 12 Out Of 20 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.