14/5 As A Mixed Number
horsecheck
Sep 23, 2025 · 6 min read
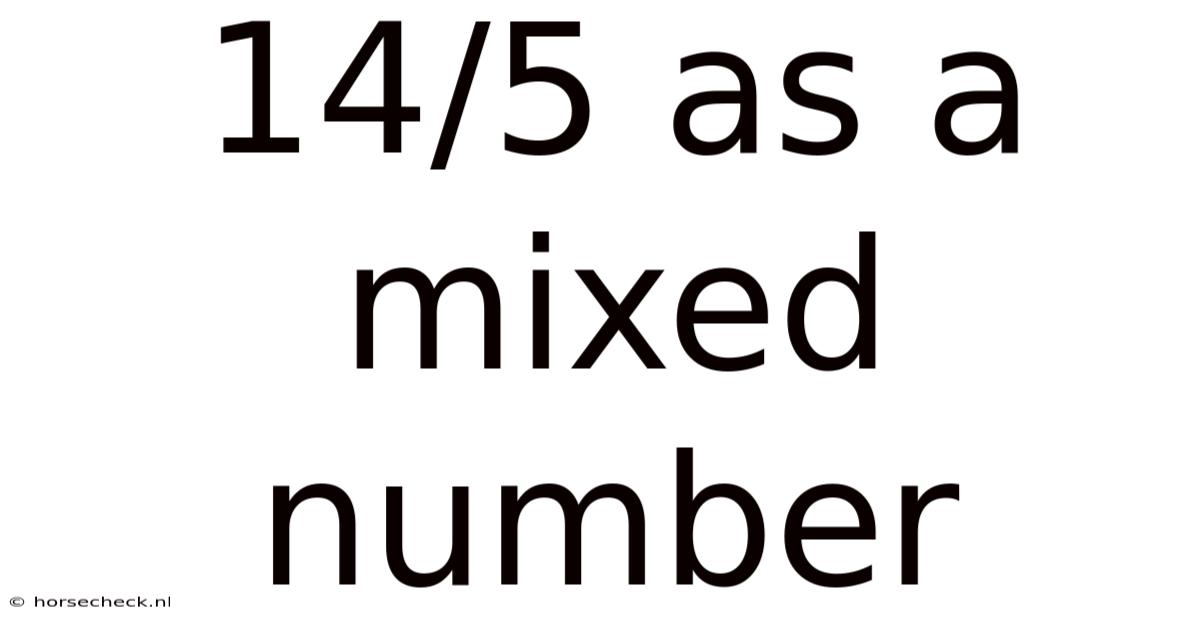
Table of Contents
Understanding 14/5 as a Mixed Number: A Comprehensive Guide
The fraction 14/5, also known as fourteen-fifths, represents a quantity larger than one whole unit. Understanding how to express this improper fraction as a mixed number is a fundamental skill in mathematics. This guide will not only show you how to convert 14/5 into a mixed number but also delve deeper into the underlying concepts, providing you with a comprehensive understanding of fractions and their various representations. We'll explore the process, offer practical examples, and address frequently asked questions. This will equip you with the confidence to tackle similar problems and build a stronger foundation in arithmetic.
Introduction to Fractions and Mixed Numbers
A fraction represents a part of a whole. It is expressed as a ratio of two integers: a numerator (top number) and a denominator (bottom number). For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This indicates three out of four equal parts.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. 14/5 is an example of an improper fraction because the numerator (14) is larger than the denominator (5). Improper fractions represent quantities greater than or equal to one whole.
A mixed number combines a whole number and a proper fraction. A proper fraction has a numerator smaller than the denominator. Mixed numbers provide a more intuitive way to represent quantities greater than one. For instance, 2 ¾ represents two whole units and three-quarters of another unit.
Converting 14/5 to a Mixed Number: Step-by-Step
Converting an improper fraction to a mixed number involves dividing the numerator by the denominator. Here's how to convert 14/5:
-
Divide the numerator by the denominator: Divide 14 by 5. This gives us a quotient of 2 and a remainder of 4.
-
Write the quotient as the whole number: The quotient (2) becomes the whole number part of the mixed number.
-
Write the remainder as the numerator of the fraction: The remainder (4) becomes the numerator of the fraction part of the mixed number.
-
Keep the original denominator: The denominator of the original fraction (5) remains the same in the mixed number.
Therefore, 14/5 as a mixed number is 2 ⁴⁄₅. This means two whole units and four-fifths of another unit.
Visual Representation of 14/5
To further solidify your understanding, let's visualize 14/5. Imagine you have 14 equal-sized pieces of a pizza. If each whole pizza consists of 5 slices, you can assemble two complete pizzas (10 slices) using 10 of those pieces. You'll have 4 slices remaining, which is ⁴⁄₅ of a pizza. This visually demonstrates why 14/5 is equivalent to 2 ⁴⁄₅.
Converting Mixed Numbers to Improper Fractions
It's equally important to understand the reverse process: converting a mixed number back into an improper fraction. This skill is crucial for performing calculations involving mixed numbers.
Let's take our mixed number, 2 ⁴⁄₅, as an example. Here's how to convert it back to an improper fraction:
-
Multiply the whole number by the denominator: Multiply 2 (the whole number) by 5 (the denominator). This gives us 10.
-
Add the numerator: Add the result (10) to the numerator of the fraction (4). This gives us 14.
-
Keep the original denominator: The denominator remains 5.
Therefore, 2 ⁴⁄₅ is equivalent to the improper fraction 14/5. This demonstrates the equivalence between the two representations.
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in everyday life and various fields:
-
Measurement: When measuring lengths, weights, or volumes, mixed numbers are often more practical than improper fractions. For example, a board measuring 2 3/8 feet is easier to understand than a board measuring 19/8 feet.
-
Cooking and Baking: Recipes often use mixed numbers for ingredient quantities. A recipe might call for 1 ½ cups of flour, which is clearer than saying 3/2 cups of flour.
-
Construction and Engineering: Mixed numbers simplify the representation of dimensions and measurements in construction and engineering projects.
-
Time: We often represent time using mixed numbers. For example, 2 hours and 30 minutes can be expressed as 2 ½ hours.
Further Exploration: Equivalent Fractions
Understanding equivalent fractions is essential for working with fractions and mixed numbers effectively. Equivalent fractions represent the same value but have different numerators and denominators. For example, 2/4, 3/6, and 4/8 are all equivalent fractions, all equal to ½.
To find equivalent fractions, you multiply or divide both the numerator and denominator by the same number (excluding zero). This maintains the ratio and, therefore, the value of the fraction. This principle can also be applied to mixed numbers by first converting them to improper fractions.
Frequently Asked Questions (FAQs)
Q1: Why is it important to understand how to convert between improper fractions and mixed numbers?
A1: Converting between these forms is crucial for simplifying calculations, comparing fractions, and expressing quantities in a clear and understandable manner. Mixed numbers are often more intuitive for everyday use, while improper fractions are more convenient for certain mathematical operations.
Q2: Can any improper fraction be converted to a mixed number?
A2: Yes, any improper fraction can be converted into a mixed number. The process of division always yields a quotient (whole number) and a remainder (forming the fractional part).
Q3: Are there any shortcuts for converting improper fractions to mixed numbers?
A3: While the long division method is always reliable, for simple cases you can sometimes mentally estimate the whole number part and then calculate the remaining fraction.
Q4: How can I check if my conversion is correct?
A4: You can always check your conversion by converting the mixed number back to an improper fraction using the method described earlier. If you obtain the original improper fraction, your conversion is correct.
Q5: What if I have a larger improper fraction, like 47/6?
A5: The same principle applies. Divide 47 by 6. You'll get a quotient of 7 and a remainder of 5. Therefore, 47/6 = 7 ⁵⁄₆. The process remains consistent regardless of the size of the numbers.
Conclusion
Understanding how to convert improper fractions to mixed numbers, and vice versa, is a fundamental skill in mathematics with wide-ranging applications. By mastering this concept, you'll enhance your ability to work with fractions, solve problems more efficiently, and gain a deeper understanding of numerical representations. Remember the simple steps involved, practice regularly, and don't hesitate to revisit the concepts and examples provided in this guide. With consistent effort, you'll build a solid foundation in arithmetic and confidently navigate the world of fractions and mixed numbers. The conversion of 14/5 to 2 ⁴⁄₅ is just one step towards building this crucial mathematical proficiency.
Latest Posts
Latest Posts
-
1 1 3 Improper Fraction
Sep 23, 2025
-
65 Percent As A Decimal
Sep 23, 2025
-
What Are The Multiples 3
Sep 23, 2025
-
Gcf Of 27 And 54
Sep 23, 2025
-
2 1 4 As Improper Fraction
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 14/5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.