17 100 As A Percent
horsecheck
Sep 25, 2025 · 5 min read
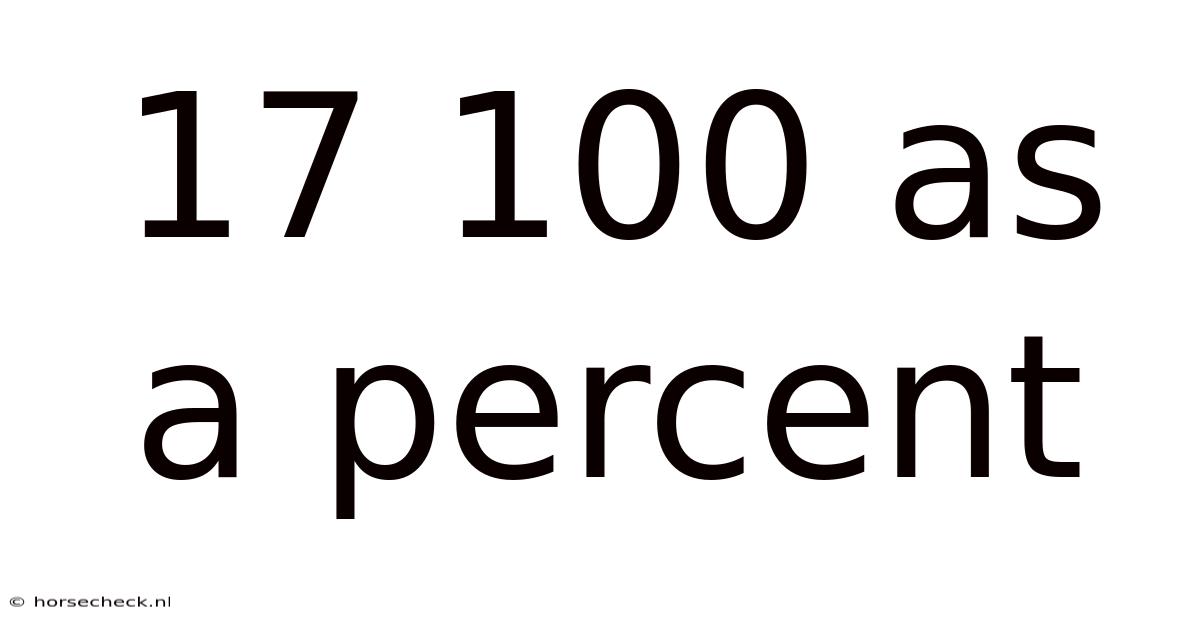
Table of Contents
17/100 as a Percent: A Comprehensive Guide to Understanding Percentages
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to analyzing data and understanding statistics. This article will delve deep into the conversion of fractions to percentages, specifically focusing on how to express 17/100 as a percent, and exploring the broader concepts surrounding percentage calculations. We’ll also address common questions and misconceptions to ensure a comprehensive understanding of this important topic.
Introduction to Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" comes from the Latin words "per centum," meaning "out of a hundred." Therefore, 17/100 represents 17 parts out of a total of 100 parts. This fractional representation can be easily converted into a percentage using a straightforward method.
Converting Fractions to Percentages: A Step-by-Step Guide
To convert a fraction like 17/100 to a percentage, you follow these steps:
-
Identify the numerator and the denominator: In the fraction 17/100, 17 is the numerator (the top number) and 100 is the denominator (the bottom number).
-
Divide the numerator by the denominator: Divide 17 by 100: 17 ÷ 100 = 0.17
-
Multiply the result by 100: Multiply the decimal obtained in step 2 by 100: 0.17 x 100 = 17
-
Add the percentage symbol (%): The final answer is 17%.
Therefore, 17/100 is equal to 17%. This simple process allows us to express the fraction as a percentage, making it easier to compare and interpret in various contexts.
Understanding the Concept of 17/100 as a Percentage
The fraction 17/100 represents a proportion or a part of a whole. Imagine you have 100 apples, and you take 17 of them. The percentage, 17%, represents the portion of the total apples you have taken. This concept extends to various scenarios:
-
Sales and Discounts: A 17% discount on an item means you pay 83% (100% - 17%) of the original price.
-
Statistics and Data Analysis: If 17 out of 100 people surveyed prefer a particular brand, this is represented as 17%.
-
Financial Calculations: Interest rates, tax rates, and profit margins are often expressed as percentages.
-
Academic Performance: A score of 17 out of 100 on a test is equivalent to 17%.
Understanding this fundamental concept is crucial for interpreting numerical data presented in percentages, which is common across various fields.
Converting Other Fractions to Percentages
The method explained above can be applied to any fraction. Let's look at a few examples:
-
25/100: 25 ÷ 100 = 0.25; 0.25 x 100 = 25%; therefore, 25/100 = 25%
-
50/100: 50 ÷ 100 = 0.50; 0.50 x 100 = 50%; therefore, 50/100 = 50%
-
75/100: 75 ÷ 100 = 0.75; 0.75 x 100 = 75%; therefore, 75/100 = 75%
-
1/4: 1 ÷ 4 = 0.25; 0.25 x 100 = 25%; therefore, 1/4 = 25% (Note: Fractions not based on 100 require the same division and multiplication steps.)
-
3/5: 3 ÷ 5 = 0.60; 0.60 x 100 = 60%; therefore, 3/5 = 60%
This illustrates the versatility of the conversion process, enabling us to express any fraction as a percentage.
Working with Percentages: Further Calculations
Once you have a percentage, you can perform various calculations:
-
Finding a percentage of a number: To find 17% of 500, you multiply 500 by 0.17 (17/100): 500 x 0.17 = 85
-
Calculating percentage increase or decrease: If a value increases from 100 to 117, the percentage increase is calculated as: [(117 - 100) / 100] x 100 = 17%
-
Determining the original value from a percentage: If 17% of a number is 85, the original number can be calculated as: 85 / 0.17 = 500
These calculations are crucial in numerous real-world situations. Mastering these allows for proficient handling of financial, statistical, and other quantitative information presented using percentages.
Scientific and Mathematical Applications of Percentages
Percentages are not merely tools for everyday calculations; they play a significant role in various scientific and mathematical fields. For instance:
-
Chemistry: Percentage composition in chemistry helps determine the relative amounts of different elements within a compound.
-
Physics: Efficiency of machines and energy conversion processes are often expressed as percentages.
-
Biology: Growth rates in populations, survival rates, and genetic inheritance are frequently analyzed using percentages.
-
Statistics and Probability: Percentages are essential for expressing probabilities and interpreting statistical data. Confidence intervals and error margins are often represented as percentages.
The importance of understanding percentages extends beyond simple arithmetic to encompass sophisticated scientific and mathematical analysis.
Frequently Asked Questions (FAQs)
Q1: Why is the percentage always out of 100?
A1: The term "percent" literally means "per hundred." The percentage system uses 100 as the base for easy comparison and interpretation of proportions.
Q2: Can I convert a decimal directly into a percentage?
A2: Yes. To convert a decimal to a percentage, simply multiply the decimal by 100 and add the % symbol. For example, 0.35 becomes 35%.
Q3: How do I convert a percentage back to a fraction?
A3: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 17% becomes 17/100, which is already in its simplest form.
Q4: What if the denominator of the fraction is not 100?
A4: If the denominator is not 100, you still follow the steps outlined earlier: divide the numerator by the denominator and then multiply by 100 to obtain the percentage.
Q5: Are there any online tools to help convert fractions to percentages?
A5: While there are many online calculators available to aid in conversions, understanding the underlying process is crucial for application in different scenarios. The manual calculation strengthens fundamental mathematical skills.
Conclusion
Understanding how to represent 17/100 as a percentage—which is 17%—is a foundational skill applicable in countless situations. This article has provided a comprehensive guide, encompassing the steps involved in conversion, explanations of underlying concepts, examples of applications, and answers to frequently asked questions. Mastering percentage calculations enhances numerical literacy and problem-solving abilities, making it a crucial skill for success in various academic and professional pursuits. The ability to accurately interpret and manipulate percentages empowers individuals to navigate a wide array of quantitative challenges effectively and confidently. Remember, consistent practice and a clear grasp of the fundamental principles will solidify your understanding of percentages and their widespread applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about 17 100 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.