2.875 As A Mixed Number
horsecheck
Sep 23, 2025 · 6 min read
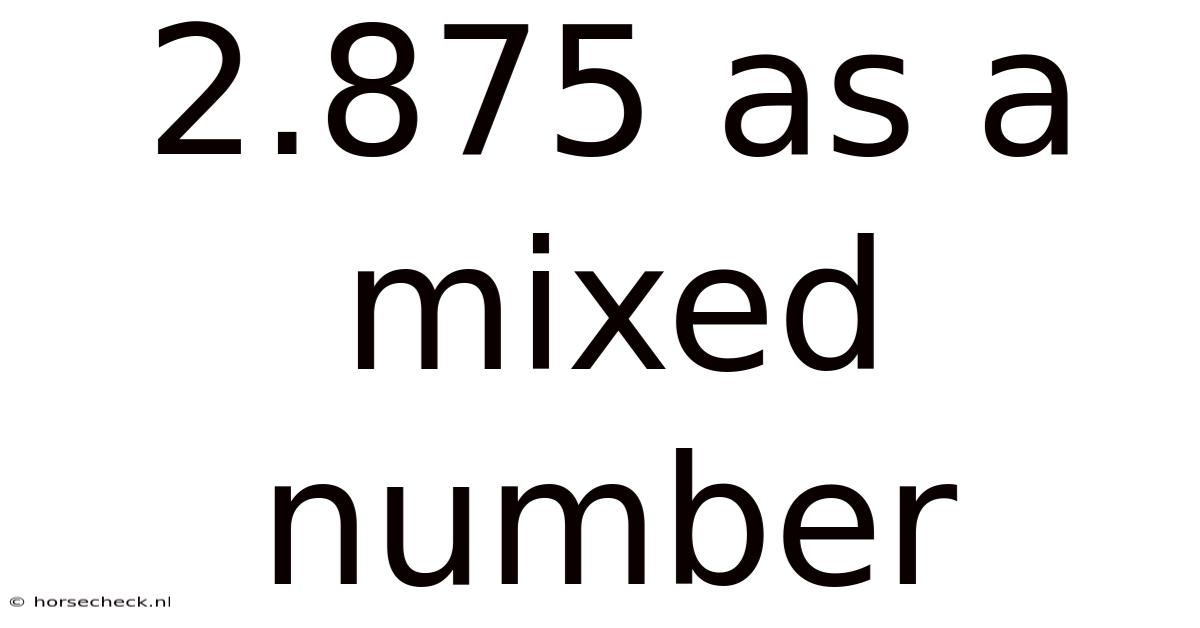
Table of Contents
Understanding 2.875 as a Mixed Number: A Comprehensive Guide
Decimals and fractions are two sides of the same coin, representing parts of a whole. Converting between them is a fundamental skill in mathematics, essential for various applications from baking to engineering. This article will provide a comprehensive guide to understanding how to convert the decimal 2.875 into a mixed number, explaining the process step-by-step and exploring the underlying mathematical principles. We will delve into the concept of mixed numbers, their significance, and practical examples to solidify your understanding. By the end, you'll not only know the answer but also confidently tackle similar conversions.
What is a Mixed Number?
Before we dive into the conversion, let's define our key term: a mixed number. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number: 2 is the whole number, and ¾ is the proper fraction. Mixed numbers are particularly useful when representing quantities that are greater than one but not a whole number. They provide a more intuitive way to represent quantities compared to improper fractions (where the numerator is greater than or equal to the denominator).
Converting 2.875 to a Fraction: A Step-by-Step Guide
The process of converting a decimal to a mixed number involves two main stages: converting the decimal to an improper fraction, and then simplifying that improper fraction into a mixed number.
Step 1: Convert the decimal to an improper fraction.
To convert the decimal 2.875 into a fraction, we first consider the place value of each digit. The number 2.875 can be written as:
2 + 0.8 + 0.07 + 0.005
This represents:
2 + 8/10 + 7/100 + 5/1000
To combine these into a single fraction, we need a common denominator. The least common multiple of 10, 100, and 1000 is 1000. Therefore, we rewrite each fraction with a denominator of 1000:
2 + (8/10 * 100/100) + (7/100 * 10/10) + 5/1000 = 2 + 800/1000 + 70/1000 + 5/1000
Adding the fractions together, we get:
2 + (800 + 70 + 5)/1000 = 2 + 875/1000
Now we have the decimal expressed as a whole number plus a fraction: 2 + 875/1000. This is an improper fraction because the whole number is combined with a fraction. However, to get a mixed number later, we can leave the whole number separate for now and concentrate on the fraction.
Step 2: Simplify the fraction.
The fraction 875/1000 can be simplified by finding the greatest common divisor (GCD) of 875 and 1000. The GCD is the largest number that divides both the numerator and the denominator evenly. One way to find the GCD is to use the prime factorization method.
- Prime factorization of 875: 5 x 5 x 5 x 7 = 5³ x 7
- Prime factorization of 1000: 2 x 2 x 2 x 5 x 5 x 5 = 2³ x 5³
The common factors are 5³, so the GCD is 5 x 5 x 5 = 125. Dividing both the numerator and denominator by 125, we get:
875 ÷ 125 = 7 1000 ÷ 125 = 8
Therefore, the simplified fraction is 7/8.
Step 3: Combine the whole number and the simplified fraction.
Now, we combine the whole number from Step 1 (2) with the simplified fraction (7/8) to obtain the mixed number:
2 + 7/8 = 2 7/8
Therefore, 2.875 as a mixed number is 2 7/8.
Alternative Method: Direct Conversion
Another approach involves directly converting the decimal part into a fraction and then simplifying. Let's explore this method:
- Isolate the decimal part: The decimal part of 2.875 is 0.875.
- Express the decimal as a fraction: This means placing the decimal part over a power of 10. In this case, 0.875 is equivalent to 875/1000.
- Simplify the fraction: As shown in the previous method, we simplify 875/1000 to 7/8 by dividing both numerator and denominator by their GCD, which is 125.
- Combine with the whole number: Add the whole number part (2) to the simplified fraction (7/8) to obtain the mixed number 2 7/8.
This method achieves the same result, showcasing the flexibility of decimal-to-fraction conversions.
The Significance of Mixed Numbers
Mixed numbers are crucial in various contexts:
-
Real-world measurements: In carpentry, cooking, or construction, we often deal with measurements that aren't whole numbers. Expressing these as mixed numbers makes them easier to understand and use. For example, a recipe might call for 2 1/2 cups of flour, which is clearer than 5/2 cups.
-
Simplifying calculations: Mixed numbers can simplify arithmetic operations, especially addition and subtraction, when compared to working solely with improper fractions.
-
Data representation: In statistics and data analysis, mixed numbers can provide a more readable representation of data points compared to solely using decimals or improper fractions.
-
Mathematical Problem Solving: Many mathematical word problems will involve using mixed numbers to represent quantities. The ability to convert between decimals and mixed numbers is critical for successful problem solving.
Frequently Asked Questions (FAQs)
Q: Can I convert any decimal to a mixed number?
A: Yes, any decimal that is greater than or equal to 1 can be converted to a mixed number. Decimals less than 1 are represented as proper fractions.
Q: What if the fraction part of the mixed number cannot be simplified?
A: If the greatest common divisor of the numerator and denominator is 1, the fraction is already in its simplest form, and no further simplification is needed.
Q: Are there other ways to convert decimals to mixed numbers?
A: While the methods described above are commonly used, alternative approaches exist, particularly involving different methods of finding the GCD.
Q: How do I convert a mixed number back to a decimal?
A: To convert a mixed number back to a decimal, divide the numerator of the fraction by the denominator and add the result to the whole number. For example, 2 7/8 is converted to a decimal by dividing 7 by 8 (0.875) and adding 2, resulting in 2.875.
Conclusion
Converting decimals to mixed numbers is a fundamental mathematical skill with practical applications in various fields. This article provided a thorough explanation of the process, including two different methods and a discussion of the importance of mixed numbers. By understanding the steps and practicing the conversions, you can confidently handle similar tasks and appreciate the versatility of different numerical representations. Remember, mastery of this skill enhances your ability to tackle more complex mathematical challenges and effectively interpret real-world data. The conversion of 2.875 to the mixed number 2 7/8 illustrates a clear and practical application of these principles. Continue practicing, and you'll soon master this important skill!
Latest Posts
Latest Posts
-
What Are The Multiples 3
Sep 23, 2025
-
Gcf Of 27 And 54
Sep 23, 2025
-
2 1 4 As Improper Fraction
Sep 23, 2025
-
Gcf Of 15 And 30
Sep 23, 2025
-
84 Out Of 100 Grade
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2.875 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.