2 Divided By 4 5
horsecheck
Sep 24, 2025 · 5 min read
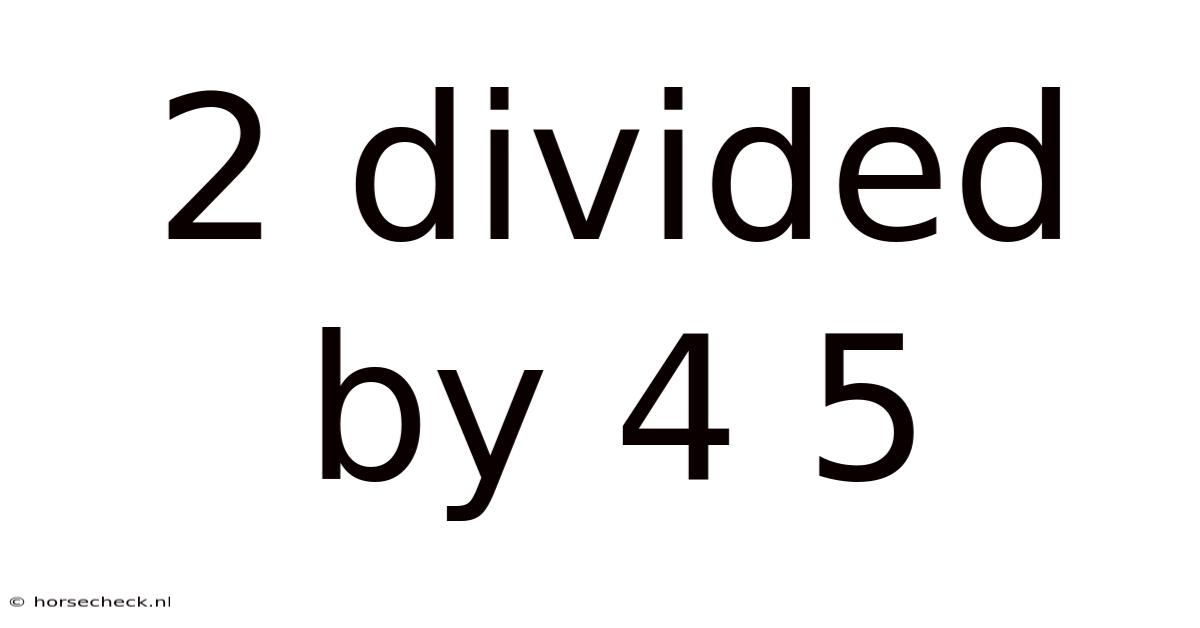
Table of Contents
Decoding 2 Divided by 4.5: A Deep Dive into Division and Decimal Operations
This article explores the seemingly simple calculation of 2 divided by 4.5, delving beyond the immediate answer to uncover the underlying mathematical principles and practical applications. We'll cover the step-by-step process, address common misconceptions, and explore the broader context of decimal division. Understanding this seemingly basic operation is fundamental to grasping more complex mathematical concepts. Whether you're a student struggling with fractions and decimals, a parent helping your child with homework, or simply curious about the intricacies of arithmetic, this guide offers a comprehensive and accessible explanation.
Understanding Division: The Basics
Before tackling 2 divided by 4.5, let's revisit the fundamental concept of division. Division is essentially the process of splitting a quantity into equal parts. For instance, if we divide 10 apples among 5 people, each person receives 2 apples (10 ÷ 5 = 2). The number being divided is called the dividend (in our example, 10), the number we're dividing by is the divisor (5), and the result is the quotient (2).
The problem 2 divided by 4.5 presents a slightly different scenario because it involves a decimal divisor. This introduces a layer of complexity that we will unravel systematically.
Step-by-Step Solution: 2 ÷ 4.5
The direct division of 2 by 4.5 can be challenging to perform mentally. However, employing a few simple techniques makes the process manageable. Here's a detailed step-by-step approach:
Method 1: Converting to Fractions
-
Represent as a fraction: The division problem 2 ÷ 4.5 can be expressed as the fraction 2/4.5.
-
Eliminate the decimal: Decimals can be cumbersome in division. To simplify, we multiply both the numerator and denominator by 10 to remove the decimal point from the denominator: (2 x 10) / (4.5 x 10) = 20/45.
-
Simplify the fraction: Now, we simplify the fraction by finding the greatest common divisor (GCD) of 20 and 45, which is 5. Dividing both the numerator and denominator by 5 gives us 4/9.
-
Convert to a decimal: Finally, to obtain the decimal equivalent, we divide 4 by 9. This results in 0.4444... (a repeating decimal). This can be represented as 0.4̅.
Method 2: Long Division
Long division is a more traditional method for solving this type of problem:
-
Set up the long division: Write 4.5 outside the long division symbol and 2 inside.
-
Adjust the divisor: Since the divisor (4.5) is a decimal, it's often helpful to adjust it to a whole number. We can multiply both the divisor and the dividend by 10: 20 ÷ 45.
-
Perform long division: Now, perform the long division as you would with whole numbers. You'll find that 45 goes into 20 zero times, so you add a decimal point and a zero to 20, making it 200. 45 goes into 200 four times (45 x 4 = 180), leaving a remainder of 20. This process repeats, giving you the repeating decimal 0.4̅.
Understanding Repeating Decimals
The result of 2 divided by 4.5 is a repeating decimal, denoted as 0.4̅. A repeating decimal is a decimal number that has a digit or group of digits that repeats infinitely. In this case, the digit "4" repeats endlessly. It's crucial to understand that this isn't a limitation of the calculation; it's an inherent property of the fraction 4/9. Many fractions, when converted to decimals, produce repeating decimals.
Practical Applications and Real-World Examples
While seemingly abstract, understanding decimal division has numerous practical applications in daily life:
-
Budgeting and Finance: Dividing expenses across multiple categories, calculating percentages of savings, or determining the cost per unit of an item all involve decimal division.
-
Cooking and Baking: Scaling recipes up or down often requires dividing or multiplying ingredient quantities, which may involve decimals.
-
Construction and Engineering: Precise measurements and calculations in construction projects rely on accurate decimal division.
-
Data Analysis and Statistics: Calculating averages, percentages, and other statistical measures frequently involves dividing numbers with decimals.
Common Mistakes and Misconceptions
Several common errors can occur when performing decimal division:
-
Incorrect Placement of the Decimal Point: Careless placement of the decimal point in the quotient is a frequent mistake.
-
Ignoring Remainders: Not properly addressing remainders in long division can lead to inaccurate results.
-
Misunderstanding Repeating Decimals: Failing to recognize and correctly represent repeating decimals can lead to misinterpretations.
Frequently Asked Questions (FAQ)
Q: Is there a way to express the answer without a repeating decimal?
A: While the decimal representation is 0.4̅, the fraction 4/9 is a more concise and exact way to express the answer without the repeating decimal.
Q: Can I use a calculator to solve this problem?
A: Yes, using a calculator is a quick and efficient method for solving this problem. However, understanding the underlying process is still crucial for developing mathematical skills.
Q: What if the dividend was a larger number?
A: The same principles apply. Whether the dividend is larger or smaller, the process of converting to a fraction, simplifying, and then converting back to a decimal (or using long division) remains consistent.
Q: Why is it important to learn this type of calculation?
A: Mastering decimal division builds a strong foundation for more advanced mathematical concepts. It's essential for problem-solving in various fields and daily life situations.
Conclusion: Mastering Decimal Division
The seemingly simple calculation of 2 divided by 4.5 offers a rich learning opportunity. We've not only found the solution (0.4̅ or 4/9) but also explored the underlying mathematical principles and real-world applications of decimal division. By understanding the step-by-step process, addressing common mistakes, and appreciating the significance of repeating decimals, you've gained a more profound understanding of this fundamental arithmetic operation. This knowledge serves as a valuable stepping stone toward tackling more complex mathematical challenges and enhancing your problem-solving abilities in various contexts. Remember, practice is key to mastering any mathematical skill. So, try some similar problems to reinforce your understanding and build your confidence.
Latest Posts
Latest Posts
-
40 42 As A Percent
Sep 24, 2025
-
51 Is Divisible By 17
Sep 24, 2025
-
31 Out Of 36 Percentage
Sep 24, 2025
-
12 Degrees F To C
Sep 24, 2025
-
Half Of 2 3 4
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 2 Divided By 4 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.