21 X What Equals 7
horsecheck
Sep 25, 2025 · 5 min read
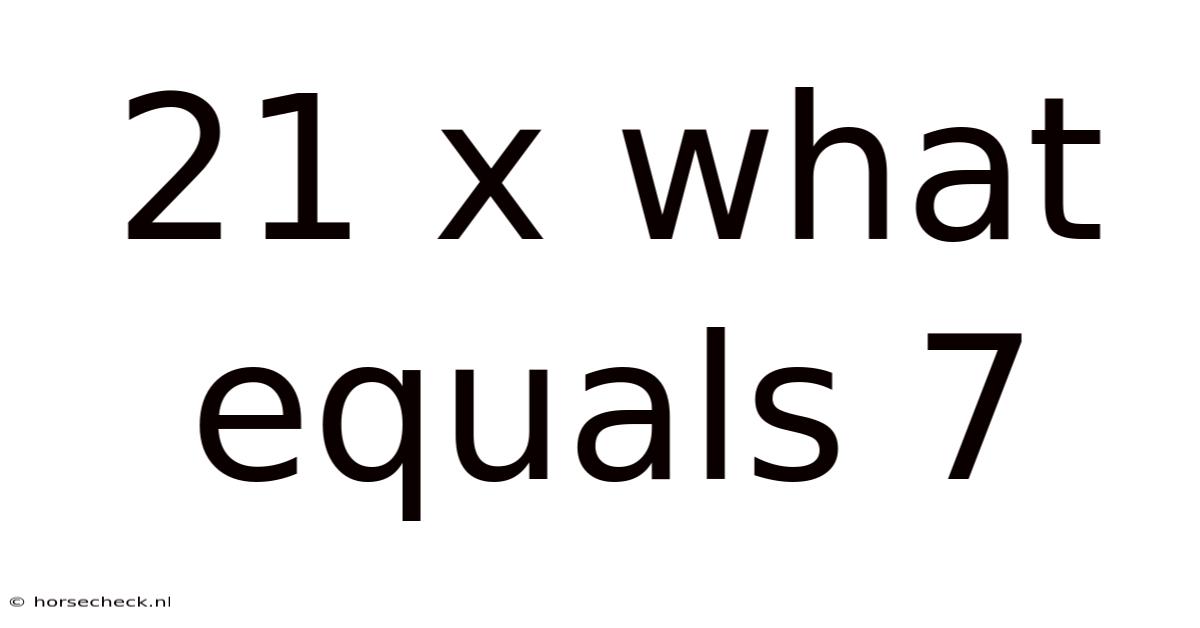
Table of Contents
21 x What Equals 7? Unlocking the Power of Algebra
Finding the missing number in the equation "21 x what equals 7" might seem like a simple arithmetic problem at first glance. However, this seemingly straightforward question opens the door to understanding fundamental algebraic concepts, problem-solving strategies, and the beauty of mathematical relationships. This article will delve into various methods for solving this equation, exploring the underlying principles, and expanding your mathematical toolkit beyond simple arithmetic.
Understanding the Problem: A Foundation in Algebra
The core of the problem "21 x what equals 7" lies in finding an unknown variable. In algebra, we often represent unknown variables with letters, most commonly 'x' or 'y'. So, we can rewrite the equation as:
21x = 7
This simple equation represents a balance: 21 multiplied by some number (x) equals 7. Our task is to find the value of 'x' that maintains this balance. This involves manipulating the equation to isolate 'x' on one side of the equals sign.
Method 1: Using Inverse Operations
The most straightforward way to solve for 'x' is to use inverse operations. Since 'x' is multiplied by 21, the inverse operation is division. To isolate 'x', we divide both sides of the equation by 21:
21x / 21 = 7 / 21
This simplifies to:
x = 7/21
Now, we simplify the fraction by finding the greatest common divisor (GCD) of 7 and 21, which is 7. Dividing both the numerator and denominator by 7, we get:
x = 1/3
Therefore, the answer to "21 x what equals 7" is 1/3. This means that 21 multiplied by one-third equals 7.
Method 2: Visualizing the Problem
For a more intuitive understanding, let's visualize the problem. Imagine you have 21 equal parts of something, and the total value of these parts is 7. To find the value of one part (x), you need to divide the total value (7) by the number of parts (21):
7 / 21 = 1/3
This visual approach reinforces the concept of division as the inverse operation of multiplication and provides a concrete representation of the abstract algebraic equation.
Method 3: Applying Proportions
Another approach involves understanding proportions. We can set up a proportion:
21/7 = 1/x
This proportion states that the ratio of 21 to 7 is equal to the ratio of 1 to x. To solve for x, we can cross-multiply:
21x = 7
Notice that this brings us back to the original equation. Solving for x using the inverse operation of division (as shown in Method 1) will yield the same result: x = 1/3.
Expanding the Understanding: Fractions and Decimals
The solution, x = 1/3, is expressed as a fraction. However, it can also be expressed as a decimal. To convert 1/3 to a decimal, we perform the division:
1 ÷ 3 ≈ 0.333...
The decimal representation of 1/3 is a repeating decimal, indicated by the ellipsis (...). This emphasizes that fractions and decimals are simply different ways of representing the same numerical value.
Beyond the Basics: Applications in Real-World Scenarios
The seemingly simple equation "21 x what equals 7" has far-reaching applications in various real-world scenarios. Here are a few examples:
-
Scaling Recipes: Imagine you have a recipe that yields 21 servings, but you only want to make 7 servings. You would need to scale down each ingredient by a factor of 1/3. This requires solving a similar equation to find the reduced quantity of each ingredient.
-
Dividing Resources: Suppose you have 21 units of a resource (e.g., money, materials, or time) and need to allocate them proportionally to complete a task requiring 7 units. Determining the portion allocated per unit requires solving an equation like this.
-
Unit Conversions: In unit conversions, similar equations arise frequently. For example, if 21 inches are equivalent to 7 centimeters, you can use this approach to find the conversion factor from inches to centimeters.
-
Data Analysis: In data analysis, such equations might emerge when scaling down data sets or adjusting variables in experiments.
Frequently Asked Questions (FAQ)
Q: Why is division used to solve this equation?
A: Division is the inverse operation of multiplication. Since the unknown variable 'x' is multiplied by 21, we use division to "undo" the multiplication and isolate 'x'.
Q: What if the equation were different, such as 7x = 21?
A: If the equation were 7x = 21, you would still use inverse operations. You would divide both sides by 7 to isolate x, resulting in x = 3.
Q: Can this problem be solved using other algebraic methods?
A: While inverse operations are the most straightforward approach, more advanced algebraic techniques, such as substitution or elimination, could be used in more complex equations. However, for this specific simple linear equation, inverse operations are the most efficient method.
Q: What if I get a negative answer?
A: If you encounter a negative answer, it simply indicates that the unknown variable represents a negative value. The process of solving the equation remains the same; inverse operations are still applied to isolate the variable.
Q: How can I practice solving similar problems?
A: Practicing with various equations involving multiplication and division will significantly improve your understanding. Start with simple equations and gradually increase the complexity. Online resources and textbooks offer numerous practice problems.
Conclusion: A Stepping Stone to Mathematical Proficiency
Solving the seemingly simple equation "21 x what equals 7" isn't just about finding the answer (1/3). It's about grasping the fundamental principles of algebra, understanding inverse operations, and appreciating the interconnectedness of mathematical concepts. The ability to solve such equations is a crucial stepping stone towards greater mathematical proficiency and the capacity to tackle more complex problems in various fields. The process of solving this equation serves as a valuable lesson in problem-solving, demonstrating how a clear understanding of mathematical principles can unlock solutions to seemingly challenging problems. By mastering this fundamental concept, you've laid a strong foundation for future mathematical endeavors.
Latest Posts
Related Post
Thank you for visiting our website which covers about 21 X What Equals 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.