3 4 X 1 2
horsecheck
Sep 21, 2025 · 6 min read
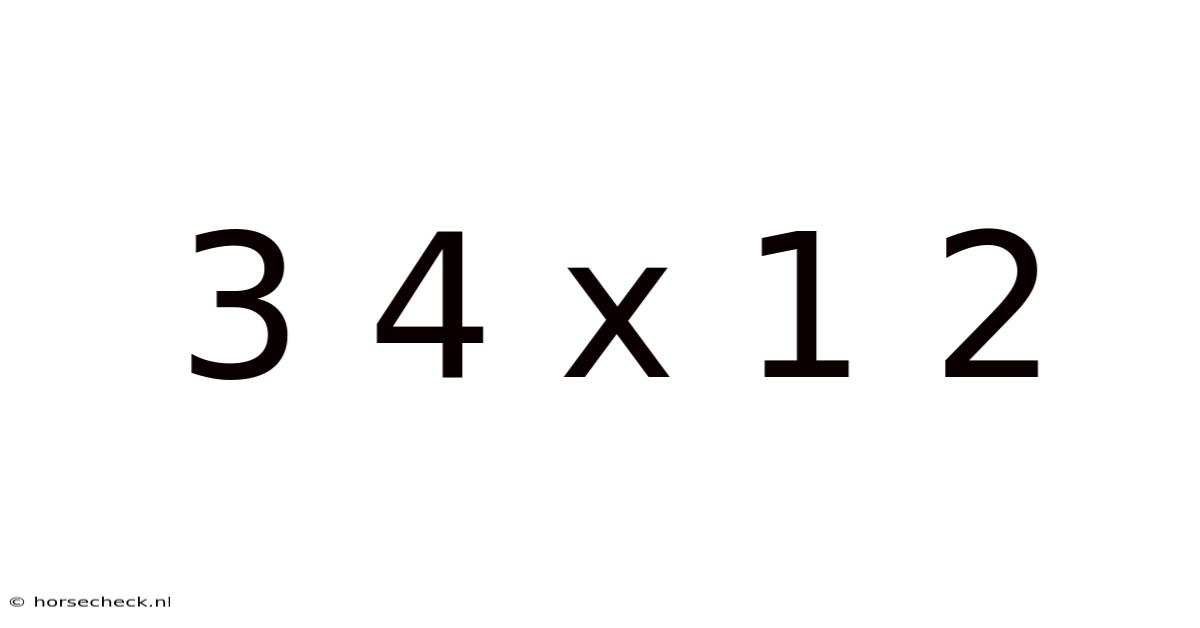
Table of Contents
Decoding 3/4 x 1/2: A Deep Dive into Fraction Multiplication
Understanding fraction multiplication can seem daunting at first, but with a clear, step-by-step approach, it becomes surprisingly straightforward. This comprehensive guide will demystify the seemingly simple problem of 3/4 x 1/2, exploring not only the mechanics of solving it but also the underlying mathematical principles and practical applications. We'll also address common misconceptions and answer frequently asked questions to ensure a complete understanding. By the end, you'll be confident in tackling any fraction multiplication problem.
Introduction: Why Fractions Matter
Fractions are fundamental to mathematics and essential for understanding many real-world scenarios. They represent parts of a whole, and mastering their manipulation is crucial for success in various fields, from cooking and construction to advanced physics and engineering. This seemingly simple problem, 3/4 x 1/2, provides a perfect entry point to explore the world of fraction arithmetic. The ability to solve this problem accurately is a building block for more complex mathematical concepts.
Understanding the Basics: Numerator and Denominator
Before we dive into the multiplication, let's review the components of a fraction. A fraction consists of two parts:
- Numerator: The top number, representing the number of parts you have. In 3/4, the numerator is 3.
- Denominator: The bottom number, representing the total number of equal parts the whole is divided into. In 3/4, the denominator is 4.
Understanding these terms is crucial for grasping fraction operations.
Method 1: Multiplying Numerators and Denominators Directly
The simplest way to multiply fractions is to multiply the numerators together and the denominators together separately. Let's apply this to our problem: 3/4 x 1/2.
- Multiply the numerators: 3 x 1 = 3
- Multiply the denominators: 4 x 2 = 8
Therefore, 3/4 x 1/2 = 3/8. This method is efficient and works for all fraction multiplications.
Method 2: Visualizing with Area Models
A visual approach can enhance understanding. Let's represent 3/4 x 1/2 using an area model.
Imagine a square representing a whole unit (1). Divide this square into four equal parts horizontally, representing the denominator of the first fraction (4). Shade three of these parts to represent the numerator of the first fraction (3). This visually represents 3/4.
Now, divide the same square into two equal parts vertically, representing the denominator of the second fraction (2). The intersection of the horizontal and vertical divisions creates smaller rectangles. The overlapping shaded area represents the product of the two fractions.
By counting the number of small rectangles in the overlapping shaded area and comparing it to the total number of small rectangles, you'll visually confirm that the answer is 3/8. This method provides a concrete visualization of the multiplication process.
Method 3: Understanding the "Of" Interpretation
Fraction multiplication can be interpreted as "of". For instance, 3/4 x 1/2 can be read as "3/4 of 1/2". This interpretation helps understand the concept. If you have 1/2 of a pizza, and you want to find 3/4 of that half, you are essentially finding a portion of a portion. The visual representation above helps solidify this concept.
Simplifying Fractions: Finding the Greatest Common Divisor (GCD)
While 3/8 is a correct answer, it's always good practice to simplify fractions to their lowest terms. This means finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it.
In the case of 3/8, the GCD of 3 and 8 is 1 (they share no common factors other than 1). Therefore, 3/8 is already in its simplest form. If the GCD was greater than 1, we would divide both the numerator and the denominator by the GCD to simplify.
Extending the Concept: Multiplying More Than Two Fractions
The principles of multiplying numerators and denominators extend to multiplying more than two fractions. For example, to solve 1/2 x 2/3 x 3/4, you would multiply all the numerators together (1 x 2 x 3 = 6) and all the denominators together (2 x 3 x 4 = 24). This results in 6/24, which simplifies to 1/4.
Real-World Applications: Where Fraction Multiplication is Used
Fraction multiplication appears in many real-world scenarios:
- Cooking: Scaling recipes up or down. If a recipe calls for 1/2 cup of flour, and you want to make 3/4 of the recipe, you'd calculate 1/2 x 3/4 = 3/8 cup of flour.
- Construction: Calculating material quantities. If a project requires 2/3 of a sheet of plywood, and you need to complete 1/2 of the project, you'll need 2/3 x 1/2 = 1/3 of a sheet.
- Finance: Calculating percentages and discounts. Finding 1/4 of a 1/2 discount means multiplying the fractions.
- Data analysis: Working with proportions and ratios in statistical analysis often requires fraction multiplication.
Common Mistakes and Misconceptions
- Adding instead of multiplying: A common mistake is to add the numerators and add the denominators. Remember, fraction multiplication involves multiplying numerators and multiplying denominators separately.
- Forgetting to simplify: Always check if the resulting fraction can be simplified to its lowest terms.
- Misinterpreting the "of" concept: Ensure a clear understanding of the "of" interpretation in fraction multiplication.
Frequently Asked Questions (FAQ)
- Q: Can I multiply fractions with different denominators? A: Yes, the method of multiplying numerators and denominators works regardless of whether the denominators are the same or different.
- Q: What if one of the numbers is a whole number? A: Express the whole number as a fraction with a denominator of 1. For example, 2 can be written as 2/1. Then, multiply as usual.
- Q: Is there a shortcut for multiplying fractions? A: Sometimes you can simplify before multiplying by canceling common factors between numerators and denominators. This is called cross-cancellation. For instance, in 1/2 x 2/3, the 2 in the numerator and the 2 in the denominator can be canceled, leaving 1/3. However, this step isn't mandatory and the direct multiplication method always works.
- Q: How do I multiply mixed numbers? A: Convert mixed numbers (e.g., 1 1/2) into improper fractions (e.g., 3/2) before multiplying.
Conclusion: Mastering Fraction Multiplication
Mastering fraction multiplication is a crucial stepping stone in your mathematical journey. By understanding the underlying principles, utilizing various solution methods (direct multiplication, area models, and the "of" interpretation), and practicing regularly, you can build a strong foundation in fractions. Remember to always simplify your answers to their lowest terms. This seemingly simple problem, 3/4 x 1/2, opens the door to a deeper appreciation of the power and elegance of mathematics and its real-world applicability. With consistent practice and a clear understanding of the concepts, you can confidently tackle any fraction multiplication problem you encounter.
Latest Posts
Latest Posts
-
Lcm Of 12 And 7
Sep 21, 2025
-
Whats 40 Percent Of 45
Sep 21, 2025
-
75 90 In Simplest Form
Sep 21, 2025
-
3 25 As A Decimal
Sep 21, 2025
-
5 6 Plus 5 6
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 3 4 X 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.