5 Divided By 3 4
horsecheck
Sep 23, 2025 · 5 min read
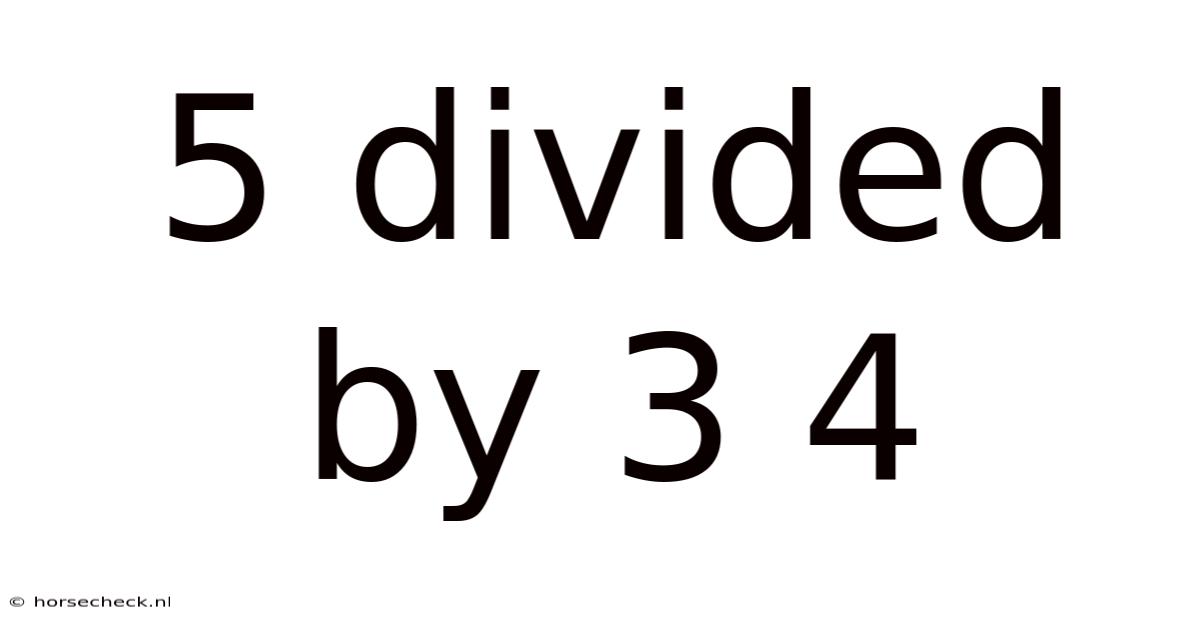
Table of Contents
Decoding 5 Divided by 3/4: A Comprehensive Guide to Fraction Division
Understanding fraction division can seem daunting, but with a clear approach, it becomes straightforward. This article delves into the process of solving 5 divided by ¾, explaining not only the steps but also the underlying mathematical principles. We'll explore various methods, address common misconceptions, and equip you with the confidence to tackle similar problems. This guide is perfect for students, teachers, or anyone seeking a deeper understanding of fraction division.
Introduction: Why Fraction Division Matters
Fraction division is a fundamental concept in mathematics with applications spanning numerous fields, from cooking and construction to advanced scientific calculations. Mastering this skill opens doors to solving complex problems involving ratios, proportions, and more. The seemingly simple problem of 5 divided by ¾, or 5 ÷ ¾, provides an excellent platform to illustrate the core principles and techniques. This article aims to demystify this calculation, explaining the "why" behind the steps as well as the "how."
Understanding the Problem: 5 ÷ ¾
Before diving into the solutions, let's break down the problem: "5 divided by ¾" means "how many ¾'s are there in 5?". This question sets the stage for our exploration of different methods to find the answer.
Method 1: The "Keep, Change, Flip" Method (Reciprocal Method)
This is arguably the most popular method for dividing fractions, and it's highly effective. The process is summarized as follows:
-
Keep: Keep the first number (the dividend) as it is. In our case, this remains 5. We can represent 5 as 5/1, a fraction where the denominator is 1.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip the second fraction (the divisor) – this means finding its reciprocal. The reciprocal of ¾ is ⁴⁄₃.
Therefore, the problem transforms from 5 ÷ ¾ to (5/1) × (⁴⁄₃).
-
Multiply: Now, multiply the numerators together and the denominators together:
(5 × 4) / (1 × 3) = 20/3
-
Simplify (if necessary): In this case, 20/3 is an improper fraction (the numerator is larger than the denominator). We can convert it to a mixed number:
20 ÷ 3 = 6 with a remainder of 2. Therefore, 20/3 = 6⅔
Therefore, 5 divided by ¾ is 6⅔.
Method 2: Using Common Denominators
This method involves converting both numbers into fractions with a common denominator before dividing.
-
Convert to Fractions: We already have ¾, and we can represent 5 as ⁵⁄₁.
-
Find a Common Denominator: The least common denominator for 1 and 3 is 3.
-
Convert Fractions to Common Denominator:
- ⁵⁄₁ becomes ¹⁵⁄₃ (multiply both numerator and denominator by 3).
- ¾ remains ¾.
-
Divide the Numerators: Now divide the numerators: 15 ÷ 3 = 5. Since the denominators are the same, they cancel out.
-
Simplify: In this case, 5 is already in its simplest form. However, if we follow the same method as in Method 1 and divide 15/3, you reach the result 5. It's important to remember this result must be further divided by the denominator. So, you are left with 5, and this is not the correct final answer. To obtain the correct final answer, you must make a minor correction in the denominator of the expression as shown below.
Correct Application of Method 2:
-
5/1 is to be divided by 3/4.
-
The reciprocal of 3/4 is 4/3. So 5/1 / 3/4 becomes 5/1 * 4/3.
-
The expression above can be simplified to 20/3 or 6 2/3.
Method 3: Visual Representation
Imagine you have 5 pizzas, and you want to divide each pizza into ¾ slices. How many ¾ slices do you have in total?
-
Slices per Pizza: Each pizza yields ⁴⁄₃ slices (because 1 pizza divided by ¾ slice size means 1 / (¾) = ⁴⁄₃ slices per pizza).
-
Total Slices: With 5 pizzas, you have 5 × ⁴⁄₃ = ²⁰⁄₃ slices.
-
Simplify: Again, ²⁰⁄₃ simplifies to 6⅔.
This visual approach helps to solidify the understanding of fraction division.
The Mathematical Explanation: Why "Keep, Change, Flip" Works
The "Keep, Change, Flip" method is a shortcut derived from the fundamental principle of dividing fractions. To divide by a fraction, we multiply by its reciprocal. This stems from the definition of division: dividing by a number is equivalent to multiplying by its multiplicative inverse (reciprocal). The reciprocal of a fraction a/b is b/a. Therefore, (a/b) ÷ (c/d) = (a/b) × (d/c).
Common Mistakes to Avoid
-
Forgetting to Flip: The most common mistake is forgetting to take the reciprocal of the second fraction before multiplying.
-
Incorrect Multiplication: Make sure to multiply numerators with numerators and denominators with denominators.
-
Improper Simplification: Ensure that the final answer is in its simplest form, either as an improper fraction or a mixed number.
Frequently Asked Questions (FAQ)
-
Q: Can I divide 5 by ¾ using decimals?
- A: Yes, you can convert the fraction ¾ to its decimal equivalent (0.75) and then perform the division: 5 ÷ 0.75 = 6.666... (approximately 6⅔). However, the fraction method is often preferred for accuracy.
-
Q: What if the divisor is a whole number?
- A: You can always treat a whole number as a fraction with a denominator of 1 (e.g., 5 = ⁵⁄₁). Then apply the "Keep, Change, Flip" method.
-
Q: What if I get a complex fraction?
- A: A complex fraction is a fraction within a fraction. To simplify, follow the steps outlined above, remembering that you will treat each portion of the fraction individually before simplifying the final fraction.
Conclusion: Mastering Fraction Division
Dividing fractions, especially a problem like 5 divided by ¾, might initially appear complicated, but the underlying principles are straightforward and logical. By mastering the “Keep, Change, Flip” method, or the common denominator approach, you gain a powerful tool for solving numerous mathematical problems. Remember to practice consistently and use various methods to solidify your understanding. This enhanced comprehension will undoubtedly empower you to confidently tackle similar problems in the future. The key is to understand the underlying mathematical concepts and choose the method that best suits your understanding and the specific problem. With practice, fraction division will become second nature!
Latest Posts
Latest Posts
-
6 And 1 2 In
Sep 23, 2025
-
1 6 As A Whole Number
Sep 23, 2025
-
Gcf Of 15 And 75
Sep 23, 2025
-
What Numbers Go Into 54
Sep 23, 2025
-
Is 91 A Irrational Number
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 5 Divided By 3 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.