6 X What Equals 42
horsecheck
Sep 25, 2025 · 6 min read
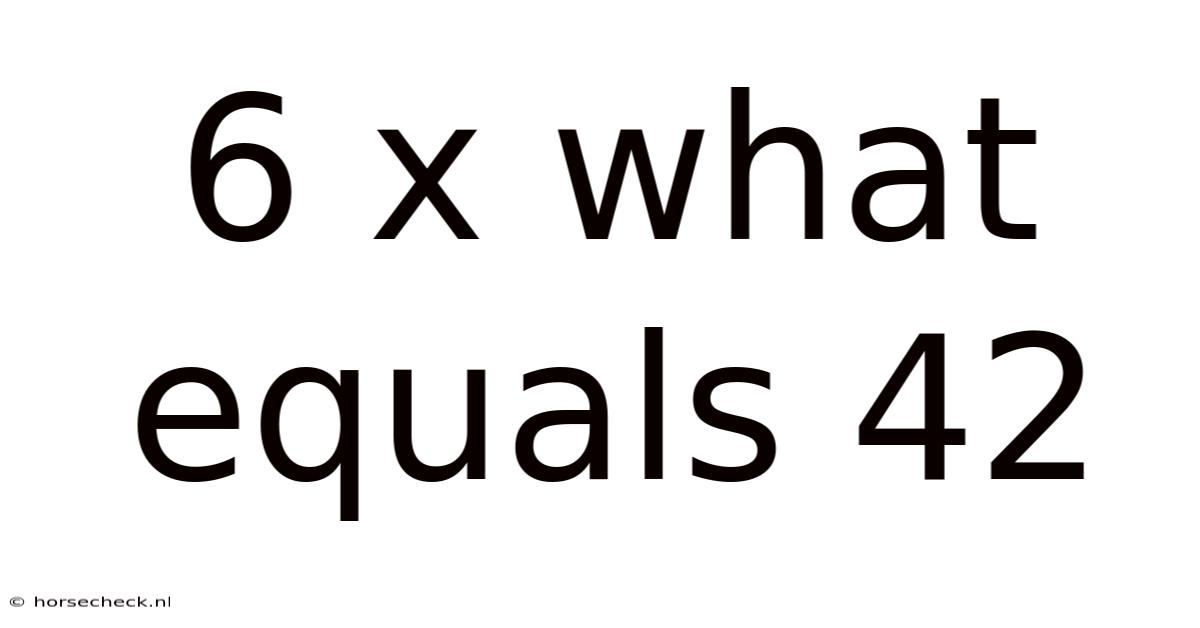
Table of Contents
Decoding the Equation: 6 x What Equals 42? A Deep Dive into Multiplication and Problem-Solving
This seemingly simple question, "6 x what equals 42?", serves as a gateway to understanding fundamental mathematical concepts, problem-solving strategies, and even the broader applications of multiplication in our everyday lives. While the answer itself is straightforward, exploring the "how" and "why" behind it unlocks a wealth of knowledge. This article will guide you through solving this equation, exploring different approaches, and delving into the underlying principles of multiplication. We'll also examine practical real-world examples and consider related mathematical concepts.
Understanding the Basics: Multiplication and Unknown Variables
At its core, the equation "6 x what equals 42" is a multiplication problem with an unknown variable. Multiplication is a fundamental arithmetic operation that represents repeated addition. For instance, 6 x 7 means adding the number 6 seven times (6 + 6 + 6 + 6 + 6 + 6 + 6 = 42). In our equation, we are looking for the number that, when multiplied by 6, results in a product of 42. This unknown number is often represented by a variable, commonly denoted by letters like x, y, or n. Therefore, our equation can be rewritten algebraically as:
6 * x = 42
Method 1: The Division Approach - Solving for the Unknown
The most direct way to solve for x in the equation 6 * x = 42 is through division. Division is the inverse operation of multiplication. To isolate x, we need to divide both sides of the equation by 6. This maintains the balance of the equation:
6 * x / 6 = 42 / 6
This simplifies to:
x = 7
Therefore, the answer to "6 x what equals 42?" is 7.
Method 2: Trial and Error - A Practical Approach
For simpler equations, the trial-and-error method can be a useful approach, particularly for those less familiar with algebraic manipulation. This involves systematically testing different numbers until you find the one that satisfies the equation. You might start by thinking:
- 6 x 1 = 6 (Too low)
- 6 x 2 = 12 (Too low)
- 6 x 3 = 18 (Too low)
- 6 x 4 = 24 (Too low)
- 6 x 5 = 30 (Too low)
- 6 x 6 = 36 (Too low)
- 6 x 7 = 42 (Correct!)
This method, while less efficient for complex equations, reinforces the concept of multiplication and helps build an intuitive understanding of numerical relationships.
Method 3: Using a Multiplication Table – A Visual Aid
Multiplication tables are a valuable tool for learning basic multiplication facts. By referring to a multiplication table, you can quickly locate the number 42 within the row or column corresponding to the number 6. The intersecting number will be the solution, which is 7. This method is particularly helpful for younger learners or for reinforcing memorized multiplication facts.
The Importance of Understanding the Underlying Principles
Solving "6 x what equals 42?" is not simply about finding the answer; it's about grasping the fundamental principles of multiplication and its relationship to division. This understanding forms the basis for more complex mathematical operations and problem-solving skills. These principles are vital across numerous fields, including:
-
Everyday Calculations: From calculating the total cost of multiple items to determining the number of tiles needed for a floor, multiplication is integral to our daily lives.
-
Finance and Budgeting: Understanding multiplication is crucial for managing personal finances, calculating interest rates, and understanding investment returns.
-
Science and Engineering: In scientific fields, multiplication is used extensively in calculations, measurements, and data analysis.
-
Computer Programming: Multiplication is a fundamental operation within computer programming, underpinning numerous algorithms and computations.
-
Geometry and Measurement: Calculating areas, volumes, and distances often requires the application of multiplication.
Expanding the Concept: Word Problems and Real-World Applications
The equation "6 x what equals 42" can be translated into various word problems to demonstrate its real-world applicability. Here are a few examples:
-
Scenario 1: A baker bakes six identical cakes per hour. How many hours will it take to bake 42 cakes? (Answer: 7 hours)
-
Scenario 2: A classroom has six rows of desks. If there are a total of 42 desks, how many desks are in each row? (Answer: 7 desks)
-
Scenario 3: You have 42 candies to distribute equally among 6 friends. How many candies does each friend receive? (Answer: 7 candies)
These examples illustrate how a simple mathematical equation can model real-world situations and help solve practical problems. The ability to translate word problems into mathematical equations is a crucial skill in problem-solving.
Beyond the Basics: Exploring Related Mathematical Concepts
Understanding the equation "6 x what equals 42" opens doors to exploring more advanced mathematical concepts:
-
Algebra: This equation is a simple algebraic equation, introducing the concept of solving for an unknown variable. As equations become more complex, algebraic techniques become increasingly important.
-
Inverse Operations: The solution relies on understanding the inverse relationship between multiplication and division. This concept extends to other mathematical operations like addition and subtraction.
-
Proportions and Ratios: This equation can be expressed as a proportion: 6/42 = 1/x. Solving for x demonstrates the principles of proportional reasoning, a crucial concept in many fields.
Frequently Asked Questions (FAQ)
Q: What is the most efficient way to solve this type of equation?
A: The most efficient method is usually division. Dividing both sides of the equation by the known multiplier (6 in this case) directly isolates the unknown variable.
Q: Can this equation be solved using other mathematical methods?
A: Yes, while division is the most direct method, trial and error or using a multiplication table are viable alternatives, particularly for simpler equations.
Q: What if the numbers were larger and more complex?
A: For larger and more complex numbers, the division method remains the most efficient. Calculators or other computational tools can be used to perform the division quickly and accurately.
Q: Why is it important to learn this type of problem?
A: This type of problem is foundational to many other mathematical concepts and is essential for solving real-world problems involving multiplication and division.
Conclusion: A Simple Equation with Profound Implications
The seemingly simple equation "6 x what equals 42?" provides a gateway to a deeper understanding of fundamental mathematical principles, problem-solving strategies, and the real-world applications of multiplication. By exploring different solution methods and related concepts, we can appreciate the broader significance of this equation and its relevance to various aspects of life. The ability to solve this equation effectively is not merely about finding the answer (7); it's about developing a strong foundation in mathematics, which empowers us to tackle more complex challenges in the future. Mastering this simple equation is a crucial step toward becoming a confident and capable problem-solver.
Latest Posts
Related Post
Thank you for visiting our website which covers about 6 X What Equals 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.