8 36 In Simplest Form
horsecheck
Sep 23, 2025 · 6 min read
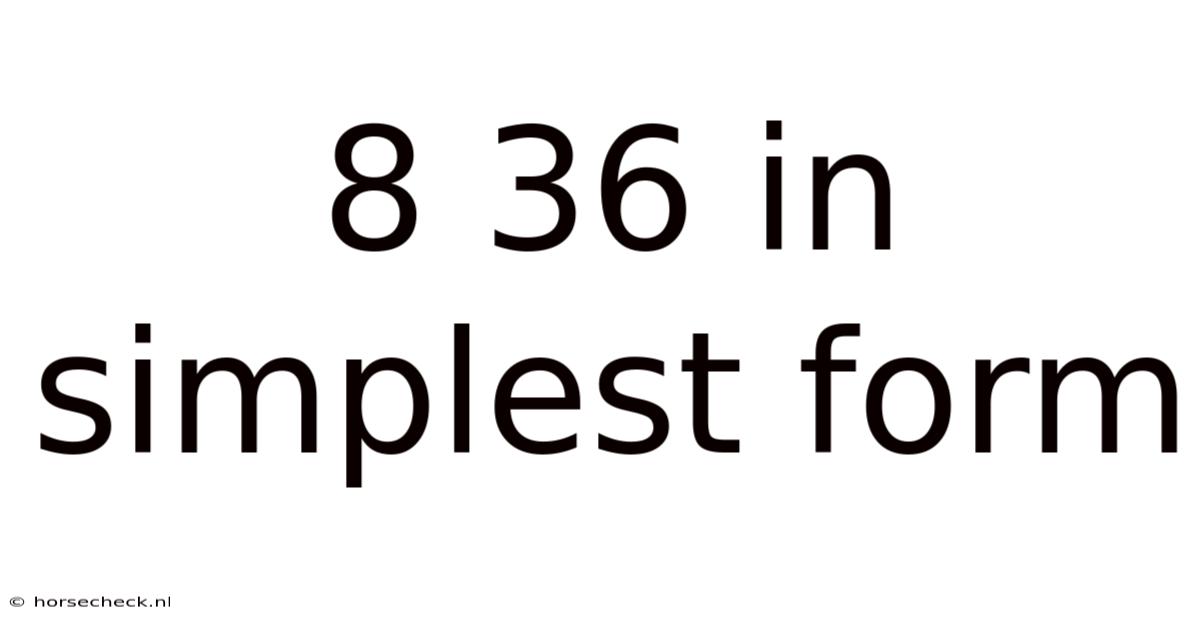
Table of Contents
Simplifying Fractions: A Deep Dive into 8/36
Understanding fractions is a cornerstone of mathematics, forming the basis for more complex concepts in algebra, calculus, and beyond. This article provides a comprehensive guide to simplifying fractions, using the example of 8/36. We'll explore the process step-by-step, delve into the underlying mathematical principles, and address frequently asked questions to ensure a thorough understanding. By the end, you'll not only know the simplest form of 8/36 but also possess the skills to simplify any fraction with confidence.
Introduction: What Does Simplifying Fractions Mean?
Simplifying a fraction, also known as reducing a fraction to its lowest terms, means finding an equivalent fraction where the numerator (the top number) and the denominator (the bottom number) have no common factors other than 1. This process doesn't change the value of the fraction; it just represents it in a more concise and manageable form. Think of it like reducing a recipe – you can halve or quarter the ingredient quantities, but the final dish will taste the same.
The fraction 8/36 represents 8 parts out of a total of 36 parts. While this is perfectly valid, it's not the most efficient representation. Simplifying helps us to work with smaller, easier-to-manage numbers, making calculations simpler and understanding clearer.
Step-by-Step Simplification of 8/36
The key to simplifying fractions is finding the greatest common divisor (GCD) or highest common factor (HCF) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
Here's how we simplify 8/36:
-
Find the factors of the numerator (8): The factors of 8 are 1, 2, 4, and 8.
-
Find the factors of the denominator (36): The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
-
Identify the common factors: Comparing the two lists, we see that the common factors of 8 and 36 are 1, 2, and 4.
-
Determine the greatest common factor (GCF): The largest common factor is 4.
-
Divide both the numerator and the denominator by the GCF:
8 ÷ 4 = 2 36 ÷ 4 = 9
Therefore, the simplified form of 8/36 is 2/9.
Alternative Method: Prime Factorization
Another powerful method for finding the GCF is through prime factorization. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11, etc.).
-
Prime factorize the numerator (8): 8 = 2 x 2 x 2 = 2³
-
Prime factorize the denominator (36): 36 = 2 x 2 x 3 x 3 = 2² x 3²
-
Identify common prime factors: Both 8 and 36 share two factors of 2 (2²).
-
Calculate the GCF: The GCF is 2 x 2 = 4.
-
Divide both the numerator and the denominator by the GCF: As before, this yields 2/9.
This method is particularly useful for larger numbers where finding all factors can be time-consuming. Prime factorization provides a systematic approach to determine the GCF efficiently.
Understanding Equivalent Fractions
It's crucial to understand that simplifying a fraction doesn't alter its value. 2/9 and 8/36 represent the same proportion or quantity. You can visualize this with a pie chart: dividing a pie into 9 equal slices and taking 2 represents the same proportion as dividing it into 36 slices and taking 8.
We can generate equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number. For example:
- 2/9 x 2/2 = 4/18
- 2/9 x 4/4 = 8/36
- 8/36 ÷ 4/4 = 2/9
This principle underscores the fundamental concept that simplifying a fraction is simply a process of finding the most concise representation of an equivalent fraction.
Applications of Fraction Simplification
Simplifying fractions is essential in various mathematical contexts:
- Arithmetic: Simplifying fractions before performing addition, subtraction, multiplication, or division makes calculations significantly easier and less prone to errors.
- Algebra: Simplifying fractions is crucial when working with rational expressions (fractions involving variables).
- Geometry: Fractions are frequently used in geometry to represent ratios and proportions (e.g., calculating the area or volume of shapes).
- Real-world applications: Fractions are used extensively in everyday life, from cooking and baking to calculating discounts and proportions in various fields.
Beyond 8/36: A General Approach to Fraction Simplification
The steps outlined above can be applied to any fraction. Here's a generalized approach:
-
Find the GCF of the numerator and denominator. You can use either the method of listing factors or prime factorization.
-
Divide both the numerator and the denominator by the GCF.
-
The resulting fraction is the simplest form.
If the GCF is 1, the fraction is already in its simplest form.
Frequently Asked Questions (FAQ)
Q: What if I divide by a common factor, but the fraction isn't fully simplified?
A: If you don't find the greatest common factor initially, you can repeat the process. Divide by another common factor until you reach a fraction where the numerator and denominator have no common factors other than 1.
Q: Is there a shortcut for simplifying fractions?
A: While there isn't a single magic shortcut, becoming proficient in recognizing small prime factors and common multiples can significantly speed up the simplification process. Practice makes perfect!
Q: Why is simplifying fractions important?
A: Simplifying fractions makes calculations easier, improves accuracy, and leads to a clearer understanding of numerical relationships and proportions.
Q: Can I simplify fractions with negative numbers?
A: Yes, the same principles apply. Simplify the numerical part of the fraction, and consider the sign separately. For instance, -8/36 simplifies to -2/9.
Q: What if the denominator is zero?
A: A fraction with a denominator of zero is undefined. Division by zero is not permitted in mathematics.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a fundamental skill in mathematics, crucial for success in numerous areas. By understanding the concept of the greatest common factor, employing prime factorization when necessary, and practicing the step-by-step process, you can master this important skill. Remember, the key is to find the greatest common divisor and divide both the numerator and the denominator by it. The resulting fraction, in this case, 2/9 for 8/36, represents the same value in a more concise and efficient manner, making further mathematical operations simpler and less prone to error. Practice regularly and soon simplifying fractions will become second nature.
Latest Posts
Latest Posts
-
What Is 80 Degrees C
Sep 23, 2025
-
What Is 95 Of 50
Sep 23, 2025
-
Convert 3 5 To Decimal
Sep 23, 2025
-
7 8 Is Equal To
Sep 23, 2025
-
45 40 As A Percent
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 8 36 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.