Gcf Of 20 And 15
horsecheck
Sep 24, 2025 · 7 min read
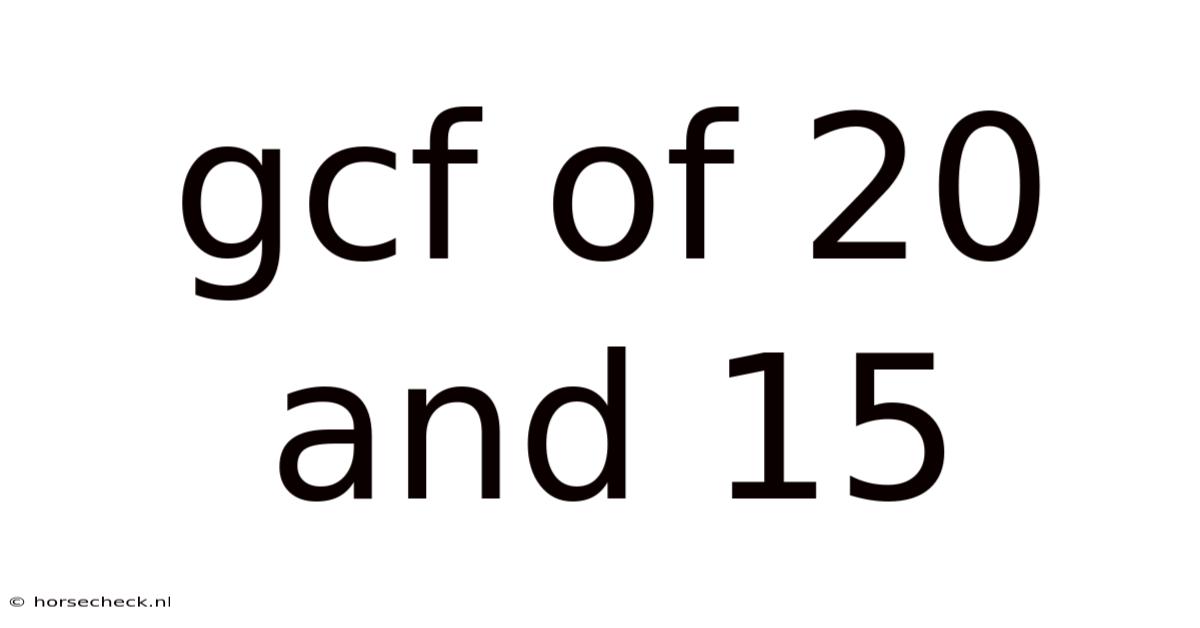
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 20 and 15: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This seemingly simple task underpins more complex mathematical operations and has practical applications in various fields. This article will delve deep into the process of finding the GCF of 20 and 15, explaining multiple methods, providing a deeper understanding of the underlying principles, and answering frequently asked questions. We will explore both manual calculation techniques and the conceptual framework behind them, making this a valuable resource for students and anyone looking to refresh their understanding of number theory.
Understanding the Greatest Common Factor (GCF)
Before we jump into calculating the GCF of 20 and 15, let's solidify our understanding of the concept. The GCF of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. It represents the largest common divisor among the given numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore, the GCF of 12 and 18 is 6.
Method 1: Listing Factors
This is the most straightforward method, especially for smaller numbers like 20 and 15. Let's list down all the factors of each number:
Factors of 20: 1, 2, 4, 5, 10, 20
Factors of 15: 1, 3, 5, 15
Now, let's identify the common factors: 1 and 5. The greatest of these common factors is 5. Therefore, the GCF of 20 and 15 is 5.
This method is simple and intuitive, but it becomes less efficient as the numbers get larger. Finding all the factors of a large number can be time-consuming.
Method 2: Prime Factorization
Prime factorization is a powerful technique for finding the GCF of larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Let's find the prime factorization of 20 and 15:
Prime factorization of 20: 2 x 2 x 5 = 2² x 5
Prime factorization of 15: 3 x 5
Now, identify the common prime factors. Both 20 and 15 share a single '5' as a prime factor. The GCF is the product of the common prime factors raised to the lowest power. In this case, the lowest power of 5 is 5¹, which simplifies to 5. Therefore, the GCF of 20 and 15 is 5.
This method is more efficient than listing factors, especially when dealing with larger numbers. The process becomes systematic and less reliant on intuition.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly useful for larger numbers. This method uses successive division until the remainder is 0. The last non-zero remainder is the GCF.
Let's apply the Euclidean algorithm to 20 and 15:
-
Divide the larger number (20) by the smaller number (15): 20 ÷ 15 = 1 with a remainder of 5.
-
Replace the larger number with the smaller number (15) and the smaller number with the remainder (5): 15 ÷ 5 = 3 with a remainder of 0.
Since the remainder is 0, the last non-zero remainder (5) is the GCF. Therefore, the GCF of 20 and 15 is 5.
The Euclidean algorithm is remarkably efficient, especially for large numbers, as it avoids the need to find all factors. It's a fundamental algorithm in number theory and has widespread applications in computer science and cryptography.
Visual Representation: Venn Diagrams
We can visualize the GCF using Venn diagrams. Represent the prime factors of each number in separate circles. The overlapping section represents the common factors.
For 20 (2 x 2 x 5) and 15 (3 x 5):
- Circle 1 (20): Contains two '2's and one '5'.
- Circle 2 (15): Contains one '3' and one '5'.
- Overlapping section: Contains one '5'.
The overlapping section represents the common prime factor, which is 5. Therefore, the GCF is 5. This visual representation provides a clear and intuitive understanding of the concept of common factors.
Real-World Applications of GCF
The GCF isn't just a theoretical concept; it has numerous practical applications:
-
Simplifying Fractions: Finding the GCF helps simplify fractions to their lowest terms. For example, the fraction 20/15 can be simplified by dividing both the numerator and denominator by their GCF (5), resulting in 4/3.
-
Dividing Objects: Imagine you have 20 apples and 15 oranges. You want to divide them into equal groups, with each group containing the same number of apples and oranges. The GCF (5) tells you that you can create 5 equal groups, each containing 4 apples and 3 oranges.
-
Measurement and Geometry: The GCF is used in solving problems related to measurement and geometry. For example, finding the largest square tile that can perfectly cover a rectangular area requires finding the GCF of the dimensions of the rectangle.
-
Music Theory: GCF plays a role in understanding musical intervals and harmonies. The relationship between different musical notes can be expressed using ratios, and simplifying these ratios often involves finding the GCF.
Understanding the Concept of Co-prime Numbers
Two numbers are considered co-prime (or relatively prime) if their greatest common factor is 1. For instance, if we were to find the GCF of 15 and 8, the prime factorization would reveal no common factors:
15 = 3 x 5 8 = 2 x 2 x 2
Since there are no common factors, the GCF is 1, making 15 and 8 co-prime numbers.
Extending the Concept to More Than Two Numbers
The methods described above can be extended to find the GCF of more than two numbers. For example, to find the GCF of 20, 15, and 30:
-
Prime Factorization:
- 20 = 2² x 5
- 15 = 3 x 5
- 30 = 2 x 3 x 5
The common prime factor is 5, and the lowest power is 5¹. Therefore, the GCF of 20, 15, and 30 is 5.
-
Euclidean Algorithm (for more than two numbers): The Euclidean algorithm can be extended iteratively. First, find the GCF of two numbers, then find the GCF of that result and the next number, and so on.
Frequently Asked Questions (FAQ)
Q1: What is the difference between GCF and LCM?
A1: The GCF (Greatest Common Factor) is the largest number that divides evenly into two or more numbers. The LCM (Least Common Multiple) is the smallest number that is a multiple of two or more numbers. They are related but distinct concepts.
Q2: Can the GCF of two numbers be larger than the smaller number?
A2: No. The GCF can never be larger than the smallest of the two numbers. This is because the GCF must be a factor of both numbers.
Q3: Is there a limit to how many times the Euclidean algorithm needs to be applied?
A3: The Euclidean algorithm will always terminate. The number of steps required depends on the size of the numbers involved. The process is guaranteed to converge to the GCF.
Q4: Are there any software or online tools to calculate GCF?
A4: Yes, many calculators and online tools are available that can calculate the GCF of numbers, often using the Euclidean algorithm or prime factorization in the background.
Conclusion
Finding the greatest common factor is a fundamental skill in mathematics with far-reaching applications. We've explored three effective methods – listing factors, prime factorization, and the Euclidean algorithm – each with its strengths and weaknesses. Understanding these methods allows you to efficiently solve problems involving GCFs, not just for simple numbers like 20 and 15, but also for much larger numbers. Remember that the core concept lies in understanding common divisors and how to identify the greatest among them, providing a solid foundation for further mathematical exploration. The visual representation using Venn diagrams further strengthens this understanding, making the concept accessible and intuitive. Mastering GCF calculations will equip you with a valuable tool for problem-solving in various mathematical and real-world contexts.
Latest Posts
Latest Posts
-
Hcf Of 8 And 12
Sep 24, 2025
-
20 25 As A Percent
Sep 24, 2025
-
Whats 30 Off Of 60
Sep 24, 2025
-
What Is 119 Divisible By
Sep 24, 2025
-
45 Degrees Celsius To F
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 20 And 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.