Percent Of 4 Is 7
horsecheck
Sep 24, 2025 · 5 min read
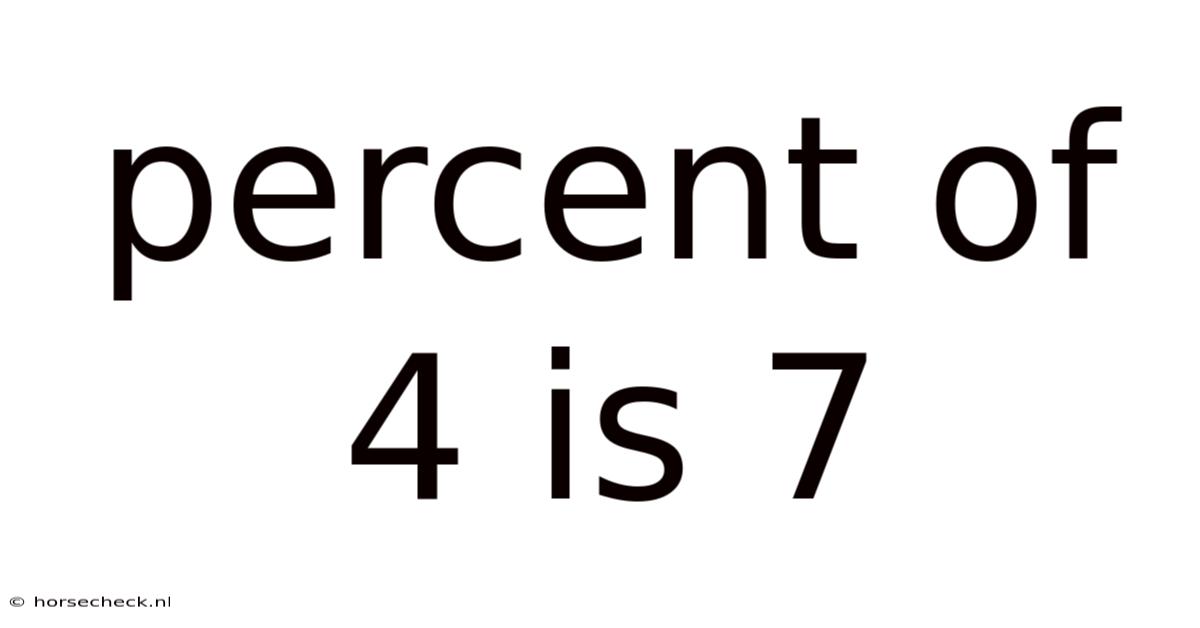
Table of Contents
Decoding the Paradox: Understanding "Percent of 4 is 7"
This seemingly simple statement, "percent of 4 is 7," presents a fascinating mathematical puzzle. At first glance, it appears contradictory. How can a percentage of a smaller number result in a larger number? This article delves into the intricacies of this problem, exploring the underlying mathematical concepts, demonstrating how to solve similar problems, and addressing common misconceptions. Understanding percentage calculations is crucial in various aspects of life, from calculating discounts to understanding financial reports. Let's unravel this mystery together.
Understanding Percentages: The Basics
Before tackling the core problem, let's solidify our understanding of percentages. A percentage is a fraction expressed as a part of 100. The symbol "%" represents "per hundred." For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5.
The basic formula for percentage calculations is:
(Part / Whole) * 100% = Percentage
Where:
- Part: Represents the portion of the whole.
- Whole: Represents the total amount.
- Percentage: The fraction expressed as a part of 100.
This formula allows us to calculate any of the three elements if we know the other two. However, the statement "percent of 4 is 7" doesn't directly fit this mold because it presents a scenario where the part (7) is larger than the whole (4). This is where the concept of relative percentages comes into play.
Reframing the Problem: Introducing Relative Percentages
The statement "percent of 4 is 7" implies a relative comparison, not a direct percentage of a whole. It's suggesting that 7 represents a certain percentage increase relative to 4. To solve this, we need to determine the percentage increase from 4 to 7.
We can achieve this by calculating the difference between 7 and 4, and then expressing this difference as a percentage of the original value (4).
Step-by-Step Solution:
-
Find the difference: Subtract the original value (4) from the final value (7): 7 - 4 = 3
-
Calculate the percentage increase: Divide the difference (3) by the original value (4) and multiply by 100%: (3/4) * 100% = 75%
Therefore, 7 represents a 75% increase relative to 4. This clarifies the statement: 7 is 75% more than 4, not 75% of 4.
Mathematical Representation and Algebraic Solution
We can represent this problem algebraically. Let 'x' be the percentage we are seeking. The equation would be:
(x/100) * 4 = 7
To solve for 'x':
-
Multiply both sides by 100: 4x = 700
-
Divide both sides by 4: x = 175
This result, 175, signifies that 175% of 4 equals 7. This is consistent with our previous calculation. 175% is composed of the original 100% (which is 4) plus an additional 75% (which is 3). The sum of 4 and 3 gives us 7.
Extending the Concept: Percentage Increase and Decrease
The "percent of 4 is 7" problem highlights the importance of understanding percentage change. This concept extends beyond simple percentage calculations and encompasses both percentage increases and decreases.
Percentage Increase: This calculates the proportional increase from an initial value to a final value. The formula is:
[(Final Value - Initial Value) / Initial Value] * 100%
Percentage Decrease: This calculates the proportional decrease from an initial value to a final value. The formula is:
[(Initial Value - Final Value) / Initial Value] * 100%
Understanding these formulas is critical in various applications, such as:
- Financial analysis: Calculating percentage changes in stock prices, profits, and investments.
- Statistical analysis: Analyzing trends and variations in data sets.
- Real-world scenarios: Determining percentage discounts, calculating interest rates, and understanding population growth or decline.
Common Misconceptions and Pitfalls
Several misconceptions can lead to errors in percentage calculations. Here are some common pitfalls to watch out for:
-
Confusing percentage of with percentage change: The most common error is to assume that "percent of 4 is 7" directly implies a simple percentage calculation. Remember to distinguish between finding a percentage of a whole and calculating a percentage change.
-
Incorrect use of the percentage formula: Ensuring you're using the correct formula (percentage of, percentage increase, or percentage decrease) based on the problem's context is vital.
-
Mathematical errors: Simple arithmetic errors can lead to incorrect results. Double-checking your calculations is always good practice.
-
Misinterpreting the problem: Always carefully read and understand the problem statement to avoid misinterpreting the question.
Practical Applications and Real-World Examples
The ability to calculate percentages accurately is essential in numerous real-world scenarios. Here are a few examples:
- Sales and discounts: Calculating the final price of an item after a discount is applied.
- Interest rates: Calculating the interest earned on a savings account or paid on a loan.
- Tax calculations: Determining the amount of tax payable on income or goods.
- Profit margins: Calculating the percentage of profit earned on a sale.
- Data analysis: Interpreting statistical data and identifying trends.
Frequently Asked Questions (FAQ)
Q: Can a percentage of a smaller number ever be larger than the number itself?
A: Yes, if we are dealing with percentage increases rather than a direct fraction of the whole. As shown in the "percent of 4 is 7" problem, a percentage increase can result in a final value larger than the initial value.
Q: What if the problem was "percent of 7 is 4"?
A: This would involve calculating a percentage decrease. The calculation would be: [(7-4)/7] * 100% = approximately 42.86%. This means 4 is approximately 42.86% of 7.
Q: How can I improve my understanding of percentage calculations?
A: Practice is key! Work through various percentage problems, focusing on identifying the type of calculation required (percentage of, increase, or decrease). Using online calculators can help check your answers and identify areas where you might need more practice.
Conclusion
The statement "percent of 4 is 7" initially presents a paradoxical situation. However, by understanding the concept of relative percentages and percentage increases, we can solve this apparent contradiction. This problem illustrates the importance of carefully analyzing the problem's context and choosing the correct mathematical approach. Mastering percentage calculations is crucial for success in various academic and professional fields, enabling individuals to confidently tackle real-world problems involving proportions and changes. Through careful analysis and application of the correct formulas, even seemingly complex percentage problems can be easily solved, fostering a deeper appreciation for the power and versatility of this fundamental mathematical concept. Remember, practice is key, and by consistently applying these principles, you will strengthen your understanding and improve your ability to solve percentage-related challenges.
Latest Posts
Latest Posts
-
Whats 3 Divided By 8
Sep 24, 2025
-
Gcf Of 18 And 15
Sep 24, 2025
-
What Is 41 Divisible By
Sep 24, 2025
-
1 8 Is What Percent
Sep 24, 2025
-
What Grade Is A 28 30
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Percent Of 4 Is 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.