Square Root Of 130 Simplified
horsecheck
Sep 23, 2025 · 4 min read
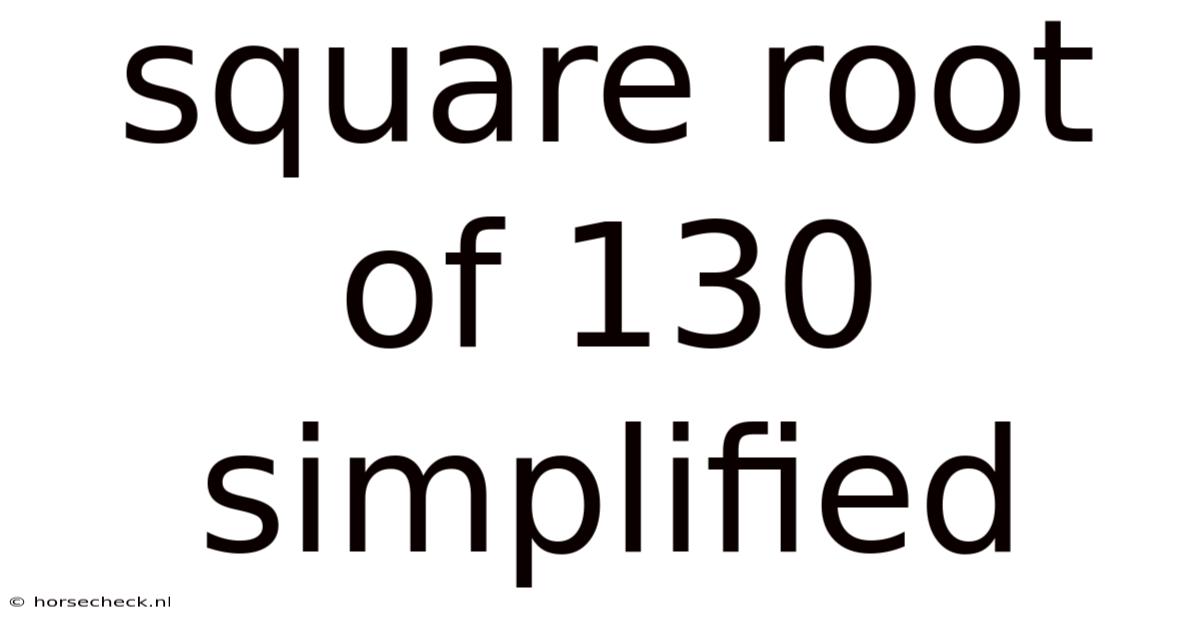
Table of Contents
Simplifying the Square Root of 130: A Comprehensive Guide
Finding the square root of 130 might seem like a straightforward task, especially with the readily available calculators. However, understanding how to simplify square roots, especially those of non-perfect squares like 130, unveils a deeper understanding of fundamental mathematical concepts. This article will guide you through the process of simplifying √130, exploring the underlying principles, and providing a comprehensive overview of the topic. We'll delve into prime factorization, the concept of simplifying radicals, and even explore the approximate decimal value for those needing a practical application.
Understanding Square Roots and Radicals
Before we tackle √130, let's refresh our understanding of square roots and radicals. A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. A radical is the symbol √ used to denote a square root. Numbers that have whole number square roots are called perfect squares (e.g., 4, 9, 16, 25, etc.). However, many numbers, like 130, are not perfect squares. This is where simplification becomes crucial.
Prime Factorization: The Key to Simplification
Simplifying a square root involves finding perfect square factors within the number. The most effective method for this is prime factorization. Prime factorization is the process of expressing a number as a product of its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.).
Let's find the prime factorization of 130:
- Start by dividing 130 by the smallest prime number, 2: 130 ÷ 2 = 65
- Now, 65 is not divisible by 2, but it is divisible by 5: 65 ÷ 5 = 13
- 13 is a prime number.
Therefore, the prime factorization of 130 is 2 x 5 x 13.
Simplifying √130
Now that we have the prime factorization of 130 (2 x 5 x 13), we look for pairs of identical prime factors. Since there are no pairs, we cannot simplify √130 further using perfect square factors. This means √130 is already in its simplest radical form.
Therefore, the simplified form of √130 is √130. There are no perfect squares that can be factored out.
Illustrative Examples: Simplifying Other Radicals
Let's look at a few examples to illustrate how simplifying works when perfect squares are present.
Example 1: Simplifying √36
- Prime factorization of 36: 2 x 2 x 3 x 3 = 2² x 3²
- We have pairs of 2 and 3. We can take one factor from each pair out of the radical: √(2² x 3²) = 2 x 3 = 6
Therefore, √36 simplifies to 6.
Example 2: Simplifying √72
- Prime factorization of 72: 2 x 2 x 2 x 3 x 3 = 2³ x 3²
- We have a pair of 2s and a pair of 3s. We can take one 2 and one 3 out of the radical: √(2³ x 3²) = 2 x 3 x √2 = 6√2
Therefore, √72 simplifies to 6√2.
Example 3: Simplifying √128
- Prime factorization of 128: 2 x 2 x 2 x 2 x 2 x 2 x 2 = 2⁷
- We have three pairs of 2s. We take one 2 from each pair out of the radical: √(2⁷) = 2 x 2 x 2 x √2 = 8√2
Therefore, √128 simplifies to 8√2.
Approximating the Decimal Value of √130
While √130 cannot be simplified further in radical form, we can approximate its decimal value using a calculator or estimation techniques. Using a calculator, we find:
√130 ≈ 11.40175
Frequently Asked Questions (FAQs)
Q1: Why can't we simply use a calculator to find the square root and consider it simplified?
While calculators provide a decimal approximation, simplifying radicals helps us understand the underlying mathematical structure and relationships between numbers. It's crucial for algebraic manipulations and solving various mathematical problems.
Q2: Are there other methods to simplify square roots besides prime factorization?
While prime factorization is the most systematic approach, you can sometimes simplify by recognizing perfect square factors directly. For example, you might notice that 72 is divisible by 36 (a perfect square), leading to the simplification 6√2.
Q3: What if the number under the radical is negative?
The square root of a negative number involves imaginary numbers, denoted by the imaginary unit i, where i² = -1. This topic falls under the realm of complex numbers and is beyond the scope of simplifying real-number radicals.
Q4: Can we simplify expressions involving multiple radicals?
Yes. The same principles apply. For instance, simplifying √(18x²y) would involve factoring and pulling out perfect square factors (9x² and leaving √(2y) within the radical.
Conclusion: Mastering Radical Simplification
Simplifying square roots, particularly those of non-perfect squares like √130, is a fundamental skill in mathematics. While √130 remains in its simplest form as √130, understanding the process of prime factorization and the logic behind simplifying radicals is essential for tackling more complex algebraic problems and gaining a deeper appreciation of number theory. Through the examples provided and the explanations offered, we hope to have given you a comprehensive understanding of how to approach this crucial topic. Remember, practice is key – try simplifying other radicals to solidify your understanding and build confidence in your mathematical abilities.
Latest Posts
Latest Posts
-
Convert 200 Fahrenheit To Celsius
Sep 23, 2025
-
3 As A Whole Number
Sep 23, 2025
-
1 888 As A Mixed Number
Sep 23, 2025
-
Convert 104 F To Celsius
Sep 23, 2025
-
Convert 230 C To Fahrenheit
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 130 Simplified . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.