What Is 1/2 Of 5
horsecheck
Sep 23, 2025 · 5 min read
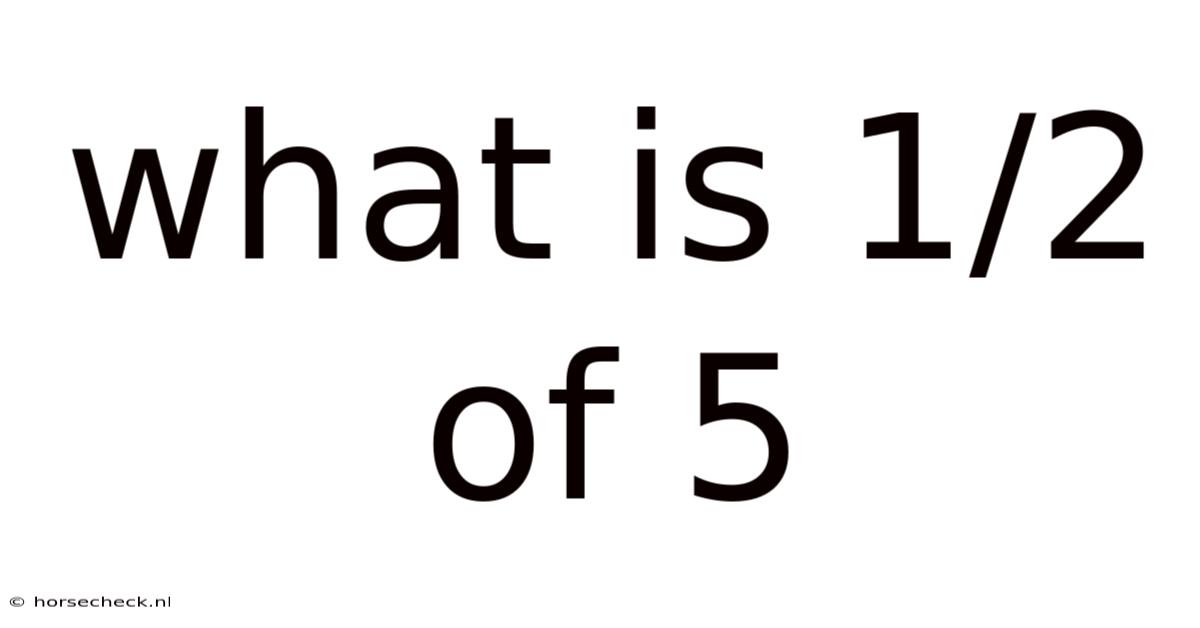
Table of Contents
What is 1/2 of 5? A Deep Dive into Fractions and Multiplication
Finding half of a number is a fundamental concept in mathematics, crucial for everyday life, from splitting bills to understanding proportions. This seemingly simple question, "What is 1/2 of 5?", opens the door to a deeper understanding of fractions, multiplication, and their practical applications. This article will explore this question in detail, providing not only the answer but also a comprehensive explanation of the underlying principles, covering various methods of calculation, and extending the concept to more complex scenarios.
Understanding Fractions: The Building Blocks
Before we tackle the problem, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts we are considering. In the fraction 1/2, the denominator (2) means the whole is divided into two equal parts, and the numerator (1) indicates we're taking one of those parts.
Method 1: Visual Representation
One of the simplest ways to understand "1/2 of 5" is through a visual representation. Imagine you have 5 apples. To find half of them, you would divide the apples into two equal groups. Each group would contain 2.5 apples. This visually demonstrates that 1/2 of 5 is 2.5. This method is particularly helpful for beginners as it provides a concrete and easily understandable approach.
Method 2: Converting to Decimal
Fractions can be easily converted to decimals. To find the decimal equivalent of 1/2, you simply divide the numerator (1) by the denominator (2): 1 ÷ 2 = 0.5. Now, multiplying this decimal by 5 gives us the answer: 0.5 x 5 = 2.5. This method relies on the understanding of decimal numbers and their relationship with fractions. It's a more abstract approach than the visual method but equally effective.
Method 3: Multiplication of Fractions
This method provides a more formal mathematical approach. We can rewrite "1/2 of 5" as a multiplication problem: (1/2) x 5. To multiply a fraction by a whole number, we can write the whole number as a fraction with a denominator of 1: (1/2) x (5/1). Now, we multiply the numerators together and the denominators together: (1 x 5) / (2 x 1) = 5/2. Finally, we convert the improper fraction 5/2 to a mixed number or decimal: 5/2 = 2 1/2 = 2.5. This method highlights the rules of fraction multiplication and demonstrates the flexibility of representing numbers in different forms.
Extending the Concept: Beyond 1/2 of 5
The principles applied to finding "1/2 of 5" can be extended to solving a wide range of similar problems. For example:
-
Finding a fraction of any number: To find a/b of c, we simply multiply the fraction a/b by the number c. For instance, to find 2/3 of 9, we calculate (2/3) x 9 = 6.
-
Finding percentages: Percentages are simply fractions with a denominator of 100. For example, 50% is equivalent to 50/100, which simplifies to 1/2. Therefore, finding 50% of a number is the same as finding 1/2 of that number.
-
Real-world applications: These calculations are vital in various situations, such as:
- Calculating discounts: Finding 25% off a $40 item.
- Sharing equally: Dividing a pizza among friends.
- Calculating proportions in recipes: Doubling or halving a recipe.
- Understanding data: Interpreting graphs and charts representing fractions or percentages.
The Importance of Understanding Fractions
A strong grasp of fractions is fundamental to mathematical proficiency. It's a stepping stone to more advanced concepts such as algebra, calculus, and statistics. Understanding fractions helps us:
-
Develop proportional reasoning: This ability allows us to solve problems involving ratios and proportions, crucial for various fields like engineering, finance, and cooking.
-
Analyze data effectively: Interpreting data presented in graphs and charts often requires understanding fractions and percentages.
-
Solve real-world problems: Many everyday situations involve fractions, from measuring ingredients to calculating discounts.
Frequently Asked Questions (FAQs)
Q: Can I use a calculator to solve this problem?
A: Yes, you can. Simply enter 0.5 * 5 or (1/2) * 5 into a calculator to get the answer 2.5. However, understanding the underlying mathematical principles is more important than simply getting the correct answer.
Q: What if the fraction is more complex, like 3/4 of 8?
A: You would follow the same principles: multiply the fraction by the whole number. (3/4) x 8 = 6. You can either multiply directly (3 x 8) / 4 = 24/4 = 6 or simplify the fraction before multiplying: (3/4) x 8 = 3 x (8/4) = 3 x 2 = 6.
Q: Why is 1/2 of 5 equal to 2.5 and not 2 or 3?
A: Because we're dividing 5 into two equal parts. Each part represents half of the whole. If we were to only take 2 whole apples, it would not represent half of 5 apples. The 0.5 represents the remaining half of an apple in each of the two groups.
Q: What are some other ways to represent 2.5?
A: 2.5 can also be represented as the mixed number 2 1/2 or the improper fraction 5/2. All three forms represent the same quantity.
Conclusion: More Than Just an Answer
The seemingly simple question, "What is 1/2 of 5?" provides a valuable opportunity to explore fundamental mathematical concepts. While the answer is 2.5, the true learning lies in understanding the methods used to arrive at the answer, the underlying principles of fractions and multiplication, and the broad applicability of these concepts in real-world scenarios. Mastering these foundational elements is crucial for success in more advanced mathematical studies and for navigating various aspects of daily life. By approaching this problem methodically, we uncover the rich mathematical landscape that lies beneath the surface of a simple arithmetic question. The ability to confidently tackle this type of problem forms the bedrock of mathematical literacy and problem-solving skills.
Latest Posts
Latest Posts
-
3 2 Divided By 3
Sep 23, 2025
-
8 22 As A Percentage
Sep 23, 2025
-
Gcf Of 4 And 6
Sep 23, 2025
-
Write 0 55 As A Fraction
Sep 23, 2025
-
85 Grados Fahrenheit A Centigrados
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/2 Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.