What Is 1/3 + 4/5
horsecheck
Sep 22, 2025 · 5 min read
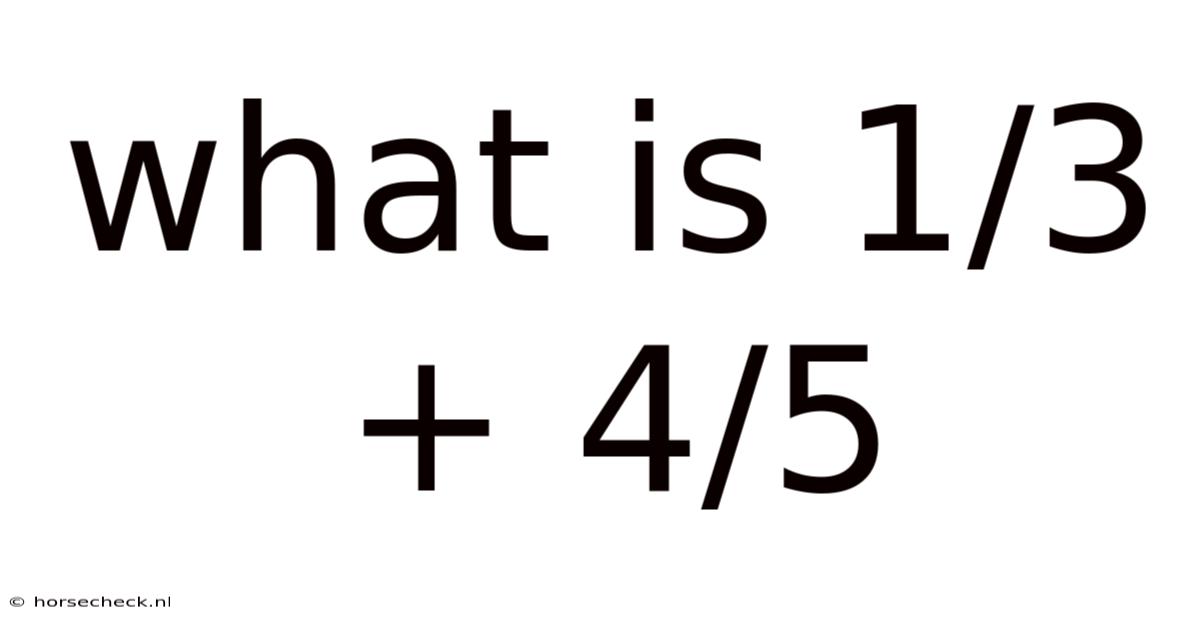
Table of Contents
What is 1/3 + 4/5? A Deep Dive into Fraction Addition
Adding fractions might seem like a simple arithmetic task, especially for those comfortable with basic math. However, understanding the underlying principles and mastering the techniques involved is crucial for building a strong foundation in mathematics. This article delves into the seemingly simple problem of adding 1/3 and 4/5, providing not only the solution but also a comprehensive explanation of the process, exploring various methods and addressing common misconceptions. This guide will leave you confident in tackling any fraction addition problem.
Understanding Fractions: A Quick Refresher
Before we tackle the addition of 1/3 and 4/5, let's review the fundamental concepts of fractions. A fraction represents a part of a whole. It consists of two main components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 1/3, the numerator (1) tells us we have one part, and the denominator (3) tells us the whole is divided into three equal parts.
The Challenge: Adding 1/3 and 4/5
The core challenge in adding 1/3 and 4/5 lies in the fact that they have different denominators. You can't simply add the numerators together (1 + 4 = 5) and keep the denominator the same (resulting in 5/8, which is incorrect). Fractions must have the same denominator before they can be added or subtracted. This common denominator represents the same size unit for both fractions, allowing for accurate comparison and summation.
Finding the Least Common Denominator (LCD)
The key to adding fractions with different denominators is finding the least common denominator (LCD). The LCD is the smallest number that is a multiple of both denominators. There are several ways to find the LCD:
-
Listing Multiples: List the multiples of each denominator until you find the smallest number that appears in both lists.
- Multiples of 3: 3, 6, 9, 12, 15, 18...
- Multiples of 5: 5, 10, 15, 20...
- The smallest common multiple is 15.
-
Prime Factorization: Break down each denominator into its prime factors. The LCD is the product of the highest powers of all prime factors present in either denominator.
- 3 = 3
- 5 = 5
- LCD = 3 x 5 = 15
For our problem, the LCD of 3 and 5 is 15.
Converting Fractions to a Common Denominator
Now that we have the LCD (15), we need to convert both 1/3 and 4/5 into equivalent fractions with a denominator of 15. To do this, we multiply both the numerator and the denominator of each fraction by the appropriate factor:
-
For 1/3: To change the denominator from 3 to 15, we multiply by 5 (because 15 / 3 = 5). Therefore, we multiply both the numerator and denominator by 5: (1 x 5) / (3 x 5) = 5/15
-
For 4/5: To change the denominator from 5 to 15, we multiply by 3 (because 15 / 5 = 3). Therefore, we multiply both the numerator and denominator by 3: (4 x 3) / (5 x 3) = 12/15
Now both fractions have the same denominator: 5/15 and 12/15.
Performing the Addition
With both fractions having the same denominator, we can now add them by simply adding the numerators and keeping the denominator the same:
5/15 + 12/15 = (5 + 12) / 15 = 17/15
Simplifying the Result (Improper Fractions and Mixed Numbers)
The result, 17/15, is an improper fraction because the numerator (17) is larger than the denominator (15). Improper fractions are often converted into mixed numbers. A mixed number combines a whole number and a proper fraction.
To convert 17/15 to a mixed number, we perform a division:
17 ÷ 15 = 1 with a remainder of 2.
This means 17/15 is equal to 1 and 2/15. Therefore:
1/3 + 4/5 = 17/15 = 1 2/15
Visual Representation
Visualizing the addition can enhance understanding. Imagine a circle divided into 15 equal parts. 5/15 represents 5 of these parts, and 12/15 represents 12 of these parts. Adding them together (5 + 12 = 17) gives you 17 parts out of 15, representing one whole circle and 2 additional parts out of 15.
Different Approaches: Using Decimal Representation
While the method above is the standard approach for adding fractions, we can also convert the fractions to decimals and then add them.
- 1/3 ≈ 0.333... (repeating decimal)
- 4/5 = 0.8
Adding the decimal representations: 0.333... + 0.8 ≈ 1.133...
This decimal approximation is consistent with our result of 1 2/15. However, it’s important to note that using decimals can sometimes lead to rounding errors, especially with repeating decimals. The fraction method provides a more precise answer.
Addressing Common Mistakes
Several common mistakes can occur when adding fractions:
- Adding numerators and denominators directly: This is incorrect. Remember, you must find a common denominator first.
- Forgetting to simplify the result: Always simplify the resulting fraction to its lowest terms (like converting 17/15 to 1 2/15).
- Incorrectly converting to a mixed number: Make sure you perform the division correctly when converting an improper fraction to a mixed number.
Frequently Asked Questions (FAQ)
-
Q: Can I add fractions with different denominators without finding the LCD? A: No. You must have a common denominator before adding or subtracting fractions.
-
Q: Is there a shortcut to finding the LCD? A: While prime factorization is generally efficient, for smaller numbers, listing multiples can be quicker.
-
Q: What if the fractions already have a common denominator? A: Simply add the numerators and keep the same denominator.
-
Q: What happens if the result is a whole number? A: The result will be a whole number if the sum of the numerators is a multiple of the denominator. For example, if the sum is 15 and the denominator is 5, the result is 3 (15/5 = 3).
Conclusion
Adding fractions, even seemingly simple ones like 1/3 + 4/5, requires a clear understanding of fundamental concepts. Mastering the process of finding the least common denominator, converting fractions to equivalent forms, and simplifying the result is crucial for success in mathematics. By carefully following these steps and understanding the underlying principles, you can confidently tackle any fraction addition problem and build a solid foundation in arithmetic. Remember to practice regularly to solidify your understanding and improve your speed and accuracy. With consistent effort, you'll find fraction addition becomes second nature.
Latest Posts
Latest Posts
-
100 150 As A Percent
Sep 22, 2025
-
165 Degrees F To Celsius
Sep 22, 2025
-
Convert 0 45 To A Fraction
Sep 22, 2025
-
14 18 As A Percentage
Sep 22, 2025
-
Write 3 5 As A Percentage
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/3 + 4/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.