What Is 1/4 Of 36
horsecheck
Sep 21, 2025 · 5 min read
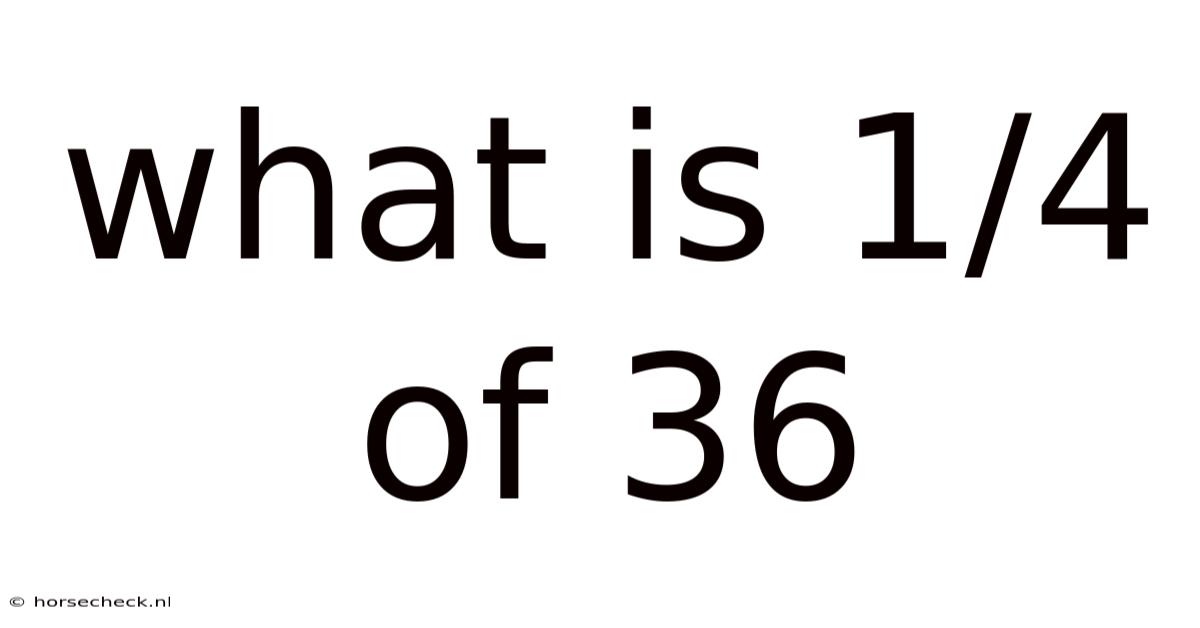
Table of Contents
What is 1/4 of 36? A Deep Dive into Fractions and Multiplication
Finding 1/4 of 36 might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this seemingly basic calculation unlocks a deeper understanding of fractions, multiplication, and their real-world applications. This article will not only answer the question "What is 1/4 of 36?" but will also delve into the underlying mathematical concepts, explore different methods of solving the problem, and offer practical examples to solidify your understanding. We’ll even touch upon advanced concepts related to fractions and their uses in various fields.
Understanding Fractions: The Building Blocks
Before we tackle the problem, let's revisit the fundamental concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts we're considering.
In our problem, 1/4 represents one out of four equal parts. The numerator is 1, and the denominator is 4. Understanding this is crucial for grasping the solution.
Method 1: Division
The most straightforward method to find 1/4 of 36 is through division. Since "of" in mathematics often signifies multiplication, the problem can be rewritten as:
1/4 * 36
To solve this, we can perform the following steps:
-
Divide the whole number by the denominator: Divide 36 by 4. This gives us 9.
-
The result is your answer: This means that 1/4 of 36 is 9.
This method leverages the understanding that finding a fraction of a number involves dividing the number by the denominator and then (if the numerator isn't 1) multiplying by the numerator. Since the numerator is 1, this step is skipped.
Method 2: Visualization
Visualizing the problem can help solidify the concept, especially for beginners. Imagine a pizza cut into four equal slices (our denominator). The whole pizza represents 36. To find 1/4 of the pizza (or 1/4 of 36), we simply divide the pizza into four equal slices. Each slice represents 1/4 of the whole. To find the value of one slice, we divide the total value (36) by the number of slices (4): 36 / 4 = 9. Therefore, one slice (1/4) of the pizza has a value of 9.
This method uses a concrete example to illustrate the abstract concept of fractions, making it easier to grasp the solution intuitively.
Method 3: Decimal Conversion
Fractions can also be expressed as decimals. To solve 1/4 of 36 using decimal conversion:
-
Convert the fraction to a decimal: 1/4 is equivalent to 0.25 (1 divided by 4).
-
Multiply the decimal by the whole number: Multiply 0.25 by 36. This gives us 9.
This approach demonstrates the interchangeability between fractions and decimals, offering another way to solve the same problem.
Expanding the Concept: Beyond 1/4 of 36
The fundamental principles used to solve "What is 1/4 of 36?" can be applied to any fraction and any whole number. Let's look at some examples:
-
Finding 2/5 of 20: First, divide 20 by the denominator (5), which equals 4. Then, multiply the result (4) by the numerator (2), which equals 8. Therefore, 2/5 of 20 is 8.
-
Finding 3/8 of 48: Divide 48 by 8 (the denominator), which is 6. Multiply 6 by 3 (the numerator), resulting in 18. So, 3/8 of 48 is 18.
These examples illustrate the general rule: To find a fraction of a whole number, divide the whole number by the denominator and multiply the result by the numerator.
Real-World Applications
The ability to calculate fractions is essential in many real-world scenarios:
-
Cooking and Baking: Recipes often require fractions of ingredients (e.g., 1/2 cup of sugar, 1/4 teaspoon of salt).
-
Shopping and Budgeting: Calculating discounts (e.g., 1/3 off), splitting bills, or understanding sales tax all involve fractions.
-
Construction and Engineering: Accurate measurements and proportions are crucial in construction, often requiring precise calculations using fractions.
-
Data Analysis: Many statistical analyses involve working with fractions and proportions of data sets.
Advanced Concepts and Further Exploration
The simple problem of finding 1/4 of 36 opens doors to more complex mathematical concepts:
-
Proportions and Ratios: Fractions are fundamental to understanding proportions and ratios, which are used extensively in various fields, from scaling maps to calculating chemical concentrations.
-
Algebra: Fractions play a key role in algebraic equations and solving for unknowns.
-
Calculus: The concepts of limits and derivatives in calculus are built upon a solid foundation in fractions and their properties.
-
Probability and Statistics: Fractions are integral to expressing probabilities and analyzing statistical data.
Frequently Asked Questions (FAQ)
Q: What if the fraction is an improper fraction (numerator greater than denominator)?
A: The same principle applies. For example, to find 5/4 of 36, you'd divide 36 by 4 (getting 9) and then multiply by 5, resulting in 45. This is larger than the original number because an improper fraction represents more than one whole.
Q: Can I use a calculator to solve fraction problems?
A: Yes, most calculators can handle fraction calculations. However, understanding the underlying concepts is crucial for problem-solving and applying these principles in different contexts.
Q: Are there any shortcuts for solving fraction problems?
A: Sometimes, simplification can be helpful. For instance, if you need to find 2/4 of a number, you can simplify the fraction to 1/2 before performing the calculation, which can make the process simpler.
Conclusion
Finding 1/4 of 36, while seemingly simple, offers a powerful entry point into the world of fractions and their applications. By understanding the different methods—division, visualization, and decimal conversion—and by practicing with various examples, you build a strong foundation for tackling more complex mathematical challenges. The ability to work with fractions is not just a mathematical skill; it's a practical tool that extends far beyond the classroom and into numerous aspects of daily life. Remember, the key to mastering fractions is understanding the underlying concepts and applying them creatively to different situations. So, continue exploring, experimenting, and expanding your understanding of this fundamental mathematical building block.
Latest Posts
Latest Posts
-
Lcm Of 12 And 7
Sep 21, 2025
-
Whats 40 Percent Of 45
Sep 21, 2025
-
75 90 In Simplest Form
Sep 21, 2025
-
3 25 As A Decimal
Sep 21, 2025
-
5 6 Plus 5 6
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/4 Of 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.