What Is 1/4 Of 40
horsecheck
Sep 22, 2025 · 5 min read
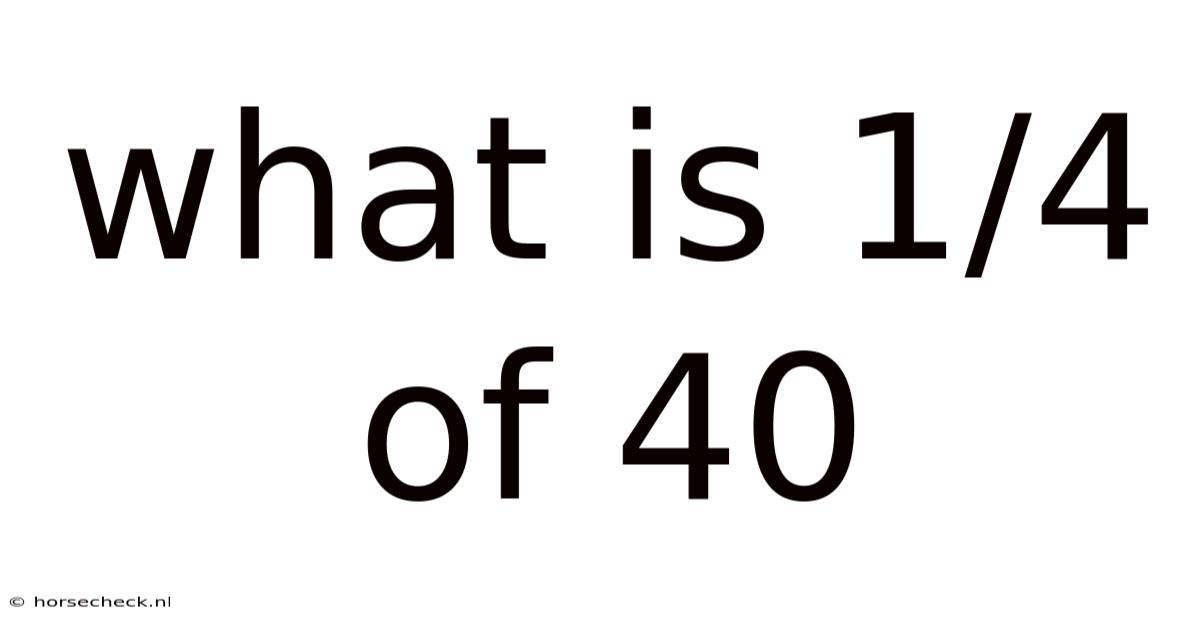
Table of Contents
What is 1/4 of 40? A Deep Dive into Fractions and Their Applications
Finding 1/4 of 40 might seem like a simple arithmetic problem, suitable only for elementary school students. However, this seemingly basic calculation opens a door to a broader understanding of fractions, their practical applications, and their importance in various fields. This article will not only answer the question directly but will also explore the underlying concepts, provide multiple solution methods, and delve into the real-world relevance of fractional calculations. Understanding fractions is crucial for everything from baking a cake to calculating financial investments.
Understanding Fractions: A Foundation
Before we tackle the problem of finding 1/4 of 40, let's establish a firm grasp of what a fraction represents. A fraction, at its core, represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator specifies how many of those parts are being considered.
In the fraction 1/4, the numerator is 1 and the denominator is 4. This means we're considering one part out of a whole that's been divided into four equal parts.
Methods to Calculate 1/4 of 40
There are several ways to calculate 1/4 of 40. Each method provides a slightly different perspective on the underlying mathematical principles.
Method 1: Direct Multiplication
The most straightforward method involves directly multiplying the fraction by the whole number:
1/4 * 40 = (1 * 40) / 4 = 40 / 4 = 10
This method highlights the fundamental operation of finding a fraction of a number: multiply the numerator by the whole number and then divide the result by the denominator.
Method 2: Division First
Alternatively, we can begin by dividing the whole number by the denominator:
40 / 4 = 10
This step gives us the value of one-fourth (1/4) of the whole. Since we are looking for one fourth, the result is already our answer. This approach emphasizes the concept of dividing the whole into equal parts.
Method 3: Visual Representation
Visualizing the problem can be particularly helpful, especially for those who are new to fractions. Imagine a rectangle divided into four equal parts. Each part represents 1/4 of the whole rectangle. If the entire rectangle represents 40 units (e.g., 40 cm, 40 apples, or 40 dollars), then each of the four equal parts would represent 10 units. Therefore, 1/4 of 40 is 10.
This visual method reinforces the conceptual understanding of fractions and provides an intuitive approach to solving the problem.
Method 4: Decimal Conversion
Fractions can also be expressed as decimals. The fraction 1/4 is equivalent to the decimal 0.25. To find 1/4 of 40, we can multiply 40 by 0.25:
40 * 0.25 = 10
This method showcases the interchangeability between fractions and decimals, emphasizing the flexibility in representing numerical values.
Expanding on the Concept: Fractions in Everyday Life
The seemingly simple calculation of 1/4 of 40 has far-reaching applications in various aspects of daily life. Here are just a few examples:
-
Cooking and Baking: Recipes often involve fractional measurements. If a recipe calls for 1/4 cup of sugar, understanding fractions is crucial for accurate measurement.
-
Shopping and Sales: Discounts are frequently expressed as fractions or percentages. A "25% off" sale is equivalent to a 1/4 discount. Calculating the final price requires understanding fractions and percentages.
-
Financial Management: Understanding fractions is essential for managing personal finances. Calculating interest rates, loan repayments, and investment returns often involve fractional calculations.
-
Construction and Engineering: Blueprints and technical drawings utilize fractions and decimals extensively. Accurate construction and engineering rely heavily on precise fractional measurements.
-
Data Analysis and Statistics: Fractions and proportions are frequently used to represent data and statistical findings. Understanding fractions is critical for interpreting and communicating statistical information.
Beyond 1/4 of 40: Exploring More Complex Fractions
The fundamental principles involved in calculating 1/4 of 40 can be extended to more complex fractional calculations. Consider the following examples:
-
Finding 3/4 of 40: This involves multiplying 3/4 by 40: (3 * 40) / 4 = 30. This illustrates that understanding the basics of 1/4 allows for easy calculations of other fractions of the same denominator.
-
Finding 1/5 of 40: This involves multiplying 1/5 by 40: (1 * 40) / 5 = 8. This shows how the same principles apply to different fractions.
-
Finding 2/5 of 40: Similar to the previous example, (2 * 40) / 5 = 16. This exemplifies the extension to more complex numerators.
Frequently Asked Questions (FAQ)
Q: What if I need to find a fraction of a number that isn't a multiple of the denominator?
A: Even if the whole number is not evenly divisible by the denominator, the same principles apply. For example, to find 1/4 of 45, you would calculate (1 * 45) / 4 = 11.25. The result might be a decimal, but the method remains the same.
Q: How do I convert fractions to percentages?
A: To convert a fraction to a percentage, you divide the numerator by the denominator and then multiply the result by 100. For example, 1/4 = (1/4) * 100 = 25%.
Q: What are some resources for learning more about fractions?
A: There are numerous online resources, educational websites, and textbooks available to help you improve your understanding of fractions.
Conclusion: The Power of Fractional Understanding
While finding 1/4 of 40 might seem trivial at first glance, it reveals the fundamental importance of understanding fractions. This basic calculation serves as a springboard to grasping more complex mathematical concepts and applying them to real-world situations. From culinary endeavors to financial planning, the ability to work with fractions is an invaluable skill with broad applications across numerous fields. Mastering fractions is not merely about solving arithmetic problems; it's about building a foundation for critical thinking and problem-solving skills applicable throughout life. The ability to break down complex problems into smaller, manageable parts, just like understanding the parts of a fraction, is a powerful tool for success in various aspects of life.
Latest Posts
Latest Posts
-
5 16ths Of An Inch
Sep 22, 2025
-
Factors Of 140 In Pairs
Sep 22, 2025
-
Factors Of 6 In Pairs
Sep 22, 2025
-
212 Degrees Fahrenheit To Celsius
Sep 22, 2025
-
What Is 12 Of 60
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/4 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.