What Is 1 7 2
horsecheck
Sep 23, 2025 · 5 min read
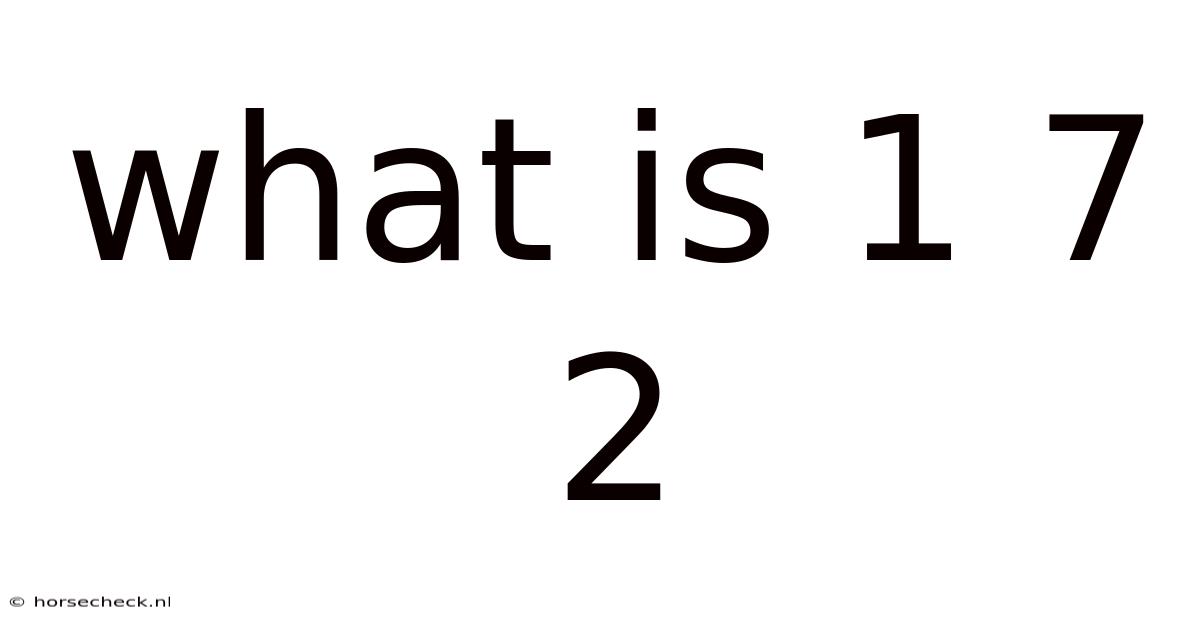
Table of Contents
Decoding the Enigma: What is 1 7 2? A Deep Dive into Number Sequences and Pattern Recognition
The seemingly simple sequence "1 7 2" might initially appear meaningless. However, this short string of numbers can open a fascinating door into the world of mathematics, pattern recognition, and problem-solving. This article will explore various interpretations of "1 7 2," delving into potential mathematical relationships, the importance of context, and the broader implications of identifying patterns in seemingly random data. We will investigate possibilities ranging from simple number sequences to more complex mathematical functions and even explore the potential for it to represent coded information. Understanding this seemingly simple sequence can reveal much about our approach to problem solving and analytical thinking.
Understanding the Limitations of Ambiguity: The Need for Context
The core challenge with interpreting "1 7 2" lies in its inherent ambiguity. Without additional context or information, numerous possibilities exist. Is it a segment of a larger sequence? Does it represent coordinates, measurements, or perhaps elements of a code? The lack of context makes definitive interpretation impossible without further clues.
This ambiguity highlights a crucial point in data analysis and problem-solving: the critical importance of context. Raw data, in its purest form, is often meaningless until its context is understood. The numbers "1 7 2" could represent entirely different things depending on the scenario. For instance, it could represent:
- Measurements: 1 meter, 7 centimeters, 2 millimeters.
- Coordinates: A point on a three-dimensional grid.
- A code: Part of a larger encryption or communication system.
- A part of a mathematical sequence: The beginning of a sequence with a hidden underlying rule.
Exploring Potential Mathematical Relationships: Sequences and Patterns
Let's explore some potential mathematical interpretations, assuming "1 7 2" is a fragment of a larger sequence. We can approach this using several methods:
-
Linear Sequences: In a linear sequence, the difference between consecutive numbers is constant. However, "1 7 2" doesn't immediately fit this pattern. The difference between 1 and 7 is 6, while the difference between 7 and 2 is -5. There's no consistent linear relationship.
-
Quadratic or Higher-Order Sequences: More complex sequences involve quadratic or higher-order relationships. To identify these, we'd need significantly more data points. With only three numbers, we can't definitively determine a higher-order relationship. We could hypothesize various quadratic or cubic equations that would fit these three points, but they wouldn't be unique solutions.
-
Recursive Sequences: Recursive sequences define each term based on previous terms. Again, with only three terms, many recursive relationships could generate "1 7 2." For example, one possible recursive rule could be: a<sub>n+1</sub> = 8 - a<sub>n</sub> - a<sub>n-1</sub> (where a<sub>1</sub>=1, a<sub>2</sub>=7). However, this is just one possibility, and many others could exist.
-
Modular Arithmetic: This branch of mathematics involves considering the remainders after division. We could explore if "1 7 2" represents remainders from a larger calculation, but this requires significant assumptions about the divisor used.
Expanding the Sequence: Hypothetical Extrapolations
To understand the underlying pattern, we need to speculate on how the sequence might continue. Let's explore several hypothetical extensions:
-
Hypothetical Extension 1: 1, 7, 2, 7, 12... This sequence exhibits a growing difference between consecutive numbers. The differences are 6, -5, 5, 10... While initially it seems chaotic, a closer inspection suggests that the differences might alternate, increasing by 11. However, this is highly speculative and requires more data points to verify.
-
Hypothetical Extension 2: 1, 7, 2, -3, -10... This extension proposes a decreasing sequence, perhaps a second-order relationship where the second difference becomes constant. Again, this is pure speculation based on limited data.
-
Hypothetical Extension 3: Considering Cyclical Patterns: It's possible that the sequence repeats itself. We could imagine the sequence as 1, 7, 2, 1, 7, 2, and so on. This kind of cyclic sequence is common in certain types of data and code.
The crucial point here is that without additional information, any of these hypothetical extensions (and many others) are equally valid. The ambiguity highlights the necessity for more data to draw conclusive results.
The Role of Context in Real-World Applications
The ambiguity illustrated by "1 7 2" is mirrored in many real-world scenarios involving data analysis and pattern recognition:
-
Cryptography: Codes and ciphers often rely on sequences of numbers. Without the key or algorithm, decoding is impossible. "1 7 2" could represent a segment of a larger encrypted message.
-
Signal Processing: In telecommunications and other fields, signals are represented as sequences of numbers. Identifying patterns in these sequences is essential for interpreting the signal's meaning. "1 7 2" might be a part of a larger signal that requires more data for complete interpretation.
-
Scientific Data: Many scientific experiments generate sequences of numerical data. Identifying patterns in this data is crucial for drawing conclusions and making predictions.
-
Financial Markets: Stock prices, interest rates, and other financial indicators form time-series data. Analyzing patterns in these sequences is crucial for financial modeling and forecasting.
Beyond Numbers: Expanding the Interpretation
Let's consider other possible interpretations, moving beyond a purely mathematical approach:
-
Representation of Objects or Events: Could "1 7 2" represent the sequence of objects or events? For example, it could be associated with specific objects, positions, or actions in a game, a puzzle, or a real-world scenario.
-
Symbolic Representation: In some cases, numbers can have symbolic meaning. "1 7 2" might not be intended as a numerical sequence but as a symbolic representation with meaning based on a specific context or system.
Conclusion: The Power of Context and Critical Thinking
The seemingly simple question, "What is 1 7 2?" reveals the crucial role of context and critical thinking in interpreting data. Without additional information, multiple interpretations are possible, highlighting the limitations of drawing conclusions from limited datasets. This ambiguity underscores the necessity of carefully considering the context and applying appropriate analytical techniques before drawing conclusions. The exercise of attempting to decode "1 7 2" demonstrates the fascinating complexities of pattern recognition and the importance of seeking additional information to reach meaningful interpretations. Further investigation, potentially involving the source of the sequence or additional data points, would be needed for a definitive answer. The journey of deciphering this seemingly simple sequence highlights the crucial role of critical thinking and contextual understanding in navigating the world of information and problem-solving.
Latest Posts
Latest Posts
-
Lcm Of 12 And 4
Sep 23, 2025
-
What Is 15 Of 22
Sep 23, 2025
-
What Percentage Is 1 8th
Sep 23, 2025
-
Whats 19 Celsius In Fahrenheit
Sep 23, 2025
-
Lcm Of 7 And 5
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 1 7 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.