What Is 15 Of 11
horsecheck
Sep 23, 2025 · 5 min read
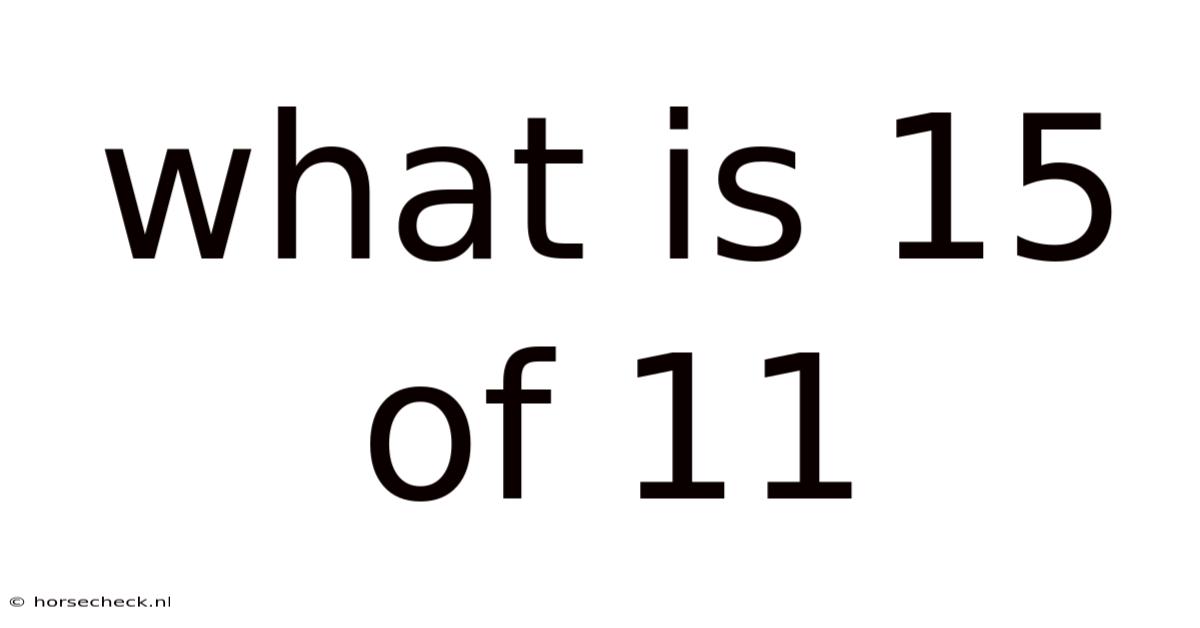
Table of Contents
What is 15 of 11? Understanding Fractions, Percentages, and Ratios
This seemingly simple question, "What is 15 of 11?", opens a door to a fundamental area of mathematics: understanding fractions, percentages, and ratios. While it might seem counterintuitive to take 15 of something that's only 11, the question highlights the importance of precisely defining mathematical operations and interpreting results within context. This article will explore various interpretations, offering a comprehensive understanding of the underlying mathematical concepts. We'll cover different approaches, including calculating fractions, converting to percentages, and considering the implications in real-world scenarios. This will be useful for students learning fractions, percentages, and ratios, as well as anyone seeking a deeper grasp of these core mathematical principles.
Introduction: The Ambiguity of "Of"
The word "of" in mathematics often signifies multiplication. However, the phrasing "15 of 11" lacks clarity. It doesn't immediately specify whether we're dealing with a fraction (15/11), a percentage (15% of 11), or another mathematical operation. To address this ambiguity, we must explore the different interpretations and their corresponding solutions.
Interpretation 1: 15/11 – A Simple Fraction
The most straightforward interpretation is that "15 of 11" represents the fraction 15/11. This is an improper fraction because the numerator (15) is larger than the denominator (11). Improper fractions are perfectly valid mathematical expressions.
To understand this fraction better, we can convert it to a mixed number. This involves dividing the numerator by the denominator:
15 ÷ 11 = 1 with a remainder of 4.
Therefore, 15/11 can be expressed as the mixed number 1 4/11. This means 15/11 is equal to one whole and four elevenths. This representation is often more intuitive when dealing with real-world quantities. For example, if you have 15 pizzas to share among 11 people, each person gets one whole pizza and 4/11 of another.
Calculating with 15/11: Working with 15/11 directly is also perfectly acceptable. If you need to perform calculations involving this fraction, you can use it in its improper form. For example:
- Adding: 15/11 + 2/11 = 17/11
- Subtracting: 15/11 - 5/11 = 10/11
- Multiplying: 15/11 * 2 = 30/11
- Dividing: 15/11 ÷ 3 = 15/33 = 5/11
Interpretation 2: 15% of 11 – A Percentage Calculation
Another interpretation is that "15 of 11" represents 15% of 11. This is a percentage calculation. To solve this, we convert the percentage to a decimal by dividing by 100:
15% = 15/100 = 0.15
Then, we multiply this decimal by 11:
0.15 * 11 = 1.65
Therefore, 15% of 11 is 1.65. This calculation is frequently used in scenarios involving discounts, taxes, or proportions. For instance, a 15% discount on an item costing $11 would result in a discount of $1.65.
Interpretation 3: Ratio – Comparing Two Quantities
"15 of 11" could also be interpreted as a ratio of 15 to 11, written as 15:11. Ratios compare the relative sizes of two or more quantities. This ratio indicates that for every 11 units of one quantity, there are 15 units of another. Ratios are extensively used in various fields like scaling, mixtures, and comparing proportions. For example, if a recipe calls for a 15:11 ratio of flour to sugar, then for every 11 units of sugar, you'd use 15 units of flour. The actual units (grams, cups, etc.) depend on the specific context.
Expanding the Understanding: Proportion and Scale
The concept of "15 of 11" can be further explored within the context of proportion and scale. Imagine we have a map where 11 centimeters represent a real-world distance of 15 kilometers. In this case, the ratio 15:11 (or 15/11) represents the scale of the map. This would allow us to calculate the real-world distance corresponding to any measured distance on the map using proportions.
For example, if a distance on the map is 22 centimeters, the corresponding real-world distance (x) can be found using the proportion:
11/15 = 22/x
Solving for x, we get:
x = (22 * 15) / 11 = 30 kilometers
This demonstrates how the understanding of fractions and ratios is crucial for dealing with scale and proportions in various applications.
Real-World Applications: Beyond the Abstract
The interpretations of "15 of 11" have practical implications across numerous real-world scenarios. Consider these examples:
- Finance: Calculating interest rates, determining profit margins, or understanding stock ratios all involve fractions and percentages.
- Cooking: Recipes frequently rely on ratios for ingredient proportions. Understanding fractions ensures accurate measurements and consistent results.
- Construction: Scale models and blueprints use ratios to represent actual building sizes. Precise calculations are essential for accurate construction.
- Science: Data analysis, particularly in experimental settings, often involves calculating ratios and proportions to understand trends and relationships.
Understanding these mathematical concepts allows for effective problem-solving in these and many other areas.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 15/11?
A: 15/11 is already in its simplest form because 15 and 11 share no common factors other than 1.
Q: How do I convert a fraction to a decimal?
A: To convert a fraction to a decimal, simply divide the numerator by the denominator. For example, 15/11 = 1.3636 (recurring).
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply by 100 and add the "%" symbol. For example, 0.15 = 15%.
Q: Can a ratio be expressed as a fraction?
A: Yes, a ratio can be expressed as a fraction. The ratio a:b is equivalent to the fraction a/b.
Q: What if "15 of 11" was intended to be a subtraction problem?
A: Then the solution would be 15 - 11 = 4. However, the phrasing "15 of 11" doesn't typically suggest subtraction. The word "of" strongly implies multiplication or a proportional relationship.
Conclusion: Context is Key
The question, "What is 15 of 11?" highlights the critical role of context in mathematical interpretation. Without a clear definition of the intended operation, multiple valid solutions exist. Understanding fractions, percentages, and ratios is essential for interpreting and solving such problems accurately. The ability to convert between these different representations is a valuable skill applicable to a wide array of disciplines and real-world situations. This analysis demonstrates that seemingly simple mathematical questions can reveal deeper layers of mathematical understanding, highlighting the importance of precise language and contextual awareness in mathematical problem-solving. Mastering these concepts provides a solid foundation for more advanced mathematical studies and problem-solving endeavors.
Latest Posts
Latest Posts
-
Gcf Of 15 And 16
Sep 23, 2025
-
250 Degrees Celsius In Fahrenheit
Sep 23, 2025
-
43 500 As A Decimal
Sep 23, 2025
-
Rewrite 17777 As A Fraction
Sep 23, 2025
-
3 2 Divided By 3
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.