What Is 15 Of 58
horsecheck
Sep 23, 2025 · 6 min read
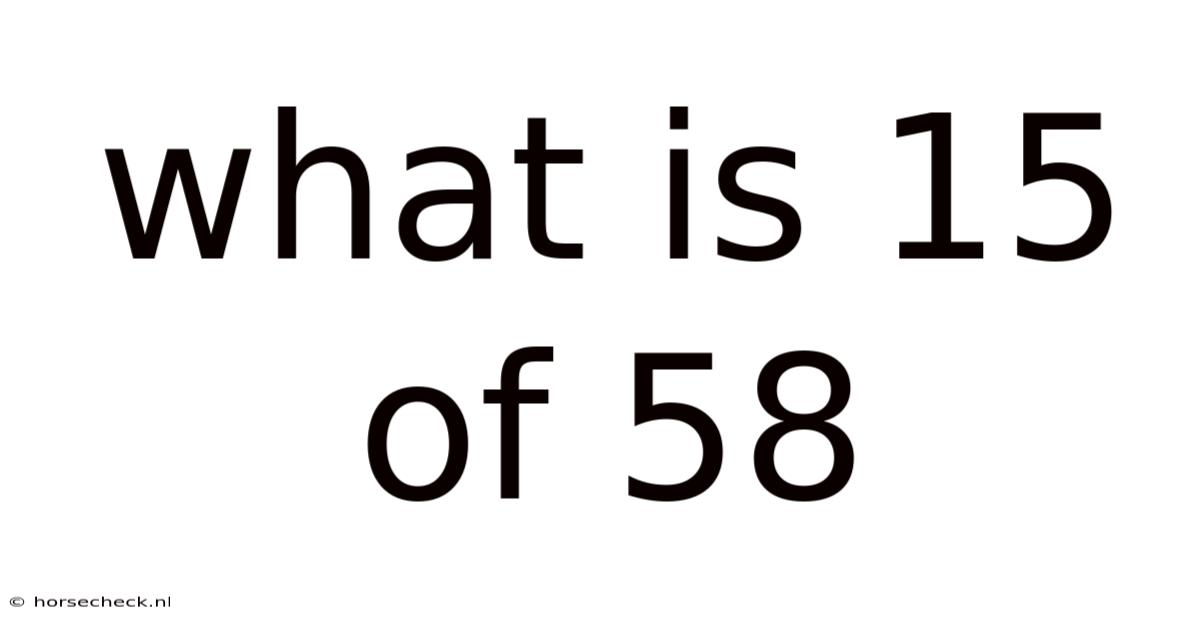
Table of Contents
What is 15 of 58? Understanding Fractions, Percentages, and Decimals
This article explores the question "What is 15 of 58?" in a comprehensive way, moving beyond a simple numerical answer to delve into the underlying mathematical concepts and practical applications. We'll examine fractions, percentages, and decimals, showing how they're interconnected and how to solve similar problems. This exploration will equip you with the tools to confidently tackle various proportional reasoning challenges.
Understanding the Problem: Fractions and Proportions
The phrase "15 of 58" inherently represents a fraction. In mathematics, a fraction expresses a part of a whole. In this case, 15 represents the part, and 58 represents the whole. We can write this as a fraction: 15/58. This fraction signifies 15 out of 58 parts.
Understanding fractions is fundamental to grasping proportions. A proportion is a statement that two ratios are equal. In our problem, we have a ratio of 15 to 58. We can use this ratio to find equivalent fractions, percentages, and decimals.
Calculating the Fraction: 15/58
The fraction 15/58 is already in its simplest form. We can't simplify it further because 15 and 58 don't share any common factors other than 1. This means the fraction is irreducible.
Converting to a Decimal: From Fraction to Decimal Representation
To convert the fraction 15/58 into a decimal, we simply divide the numerator (15) by the denominator (58):
15 ÷ 58 ≈ 0.2586
The result is an approximation because the decimal representation of 15/58 is a non-terminating, repeating decimal. This means the digits after the decimal point go on infinitely without ever forming a repeating pattern that terminates. For most practical purposes, rounding to a certain number of decimal places (e.g., 0.2586) is sufficient. The more decimal places you use, the more accurate your approximation will be.
Converting to a Percentage: Expressing the Proportion as a Percentage
A percentage expresses a fraction as parts per hundred. To convert the fraction 15/58 to a percentage, we can first convert it to a decimal (as shown above) and then multiply by 100%:
0.2586 × 100% ≈ 25.86%
Therefore, 15 out of 58 represents approximately 25.86%.
Real-World Applications: Understanding Proportions in Context
The concept of "15 of 58" is applicable in various real-world scenarios. Consider the following examples:
-
Test Scores: Imagine a test with 58 questions. If a student answered 15 questions correctly, their score would be 15/58, or approximately 25.86%.
-
Survey Results: In a survey of 58 people, if 15 responded positively to a particular question, then 15/58 or approximately 25.86% of respondents gave a positive response.
-
Inventory Management: If a warehouse contains 58 units of a particular item, and 15 are damaged, the proportion of damaged items is 15/58, or approximately 25.86%.
-
Financial Calculations: In investment scenarios, this concept could be used for calculating the percentage of total assets invested in a particular sector.
These examples demonstrate how understanding fractions, decimals, and percentages is crucial for interpreting and applying proportional reasoning in diverse contexts.
Further Mathematical Explorations: Beyond the Basics
While the core question addresses a straightforward calculation, it opens doors to more advanced mathematical concepts:
-
Ratio and Proportion Problems: The problem is a simple example of a ratio and proportion problem. More complex problems might involve finding an unknown quantity given other proportional relationships. For instance, if 15 out of 58 people prefer brand A, and we have a larger sample of 290 people, how many would we expect to prefer brand A? (The answer involves setting up a proportion and solving for the unknown quantity).
-
Percentage Change: We could extend this to calculate percentage changes. For example, if the number of positive responses in a survey increased from 15 out of 58 to 20 out of 58, we could calculate the percentage increase.
-
Statistical Analysis: In statistics, fractions and percentages are fundamental tools for presenting and interpreting data. Understanding proportions is critical for analyzing datasets and drawing meaningful conclusions.
-
Probability: The fraction 15/58 could represent a probability. If there are 58 equally likely outcomes, and 15 of them represent a particular event, then the probability of that event occurring is 15/58.
Expanding Your Mathematical Skills: Practice and Resources
To solidify your understanding of fractions, decimals, and percentages, it's crucial to engage in consistent practice. Here are some ways to improve:
-
Solve Practice Problems: Seek out online resources, textbooks, or workbooks that provide numerous practice problems involving fractions, decimals, and percentages. Working through various problems will reinforce your understanding of the concepts and improve your calculation skills.
-
Use Online Calculators: Online calculators can be helpful for checking your answers and verifying your calculations, but always ensure you understand the underlying mathematical processes.
-
Seek Additional Learning Resources: Explore educational websites, videos, and tutorials that offer comprehensive explanations of fractions, decimals, and percentages. These resources can provide visual aids and interactive exercises to deepen your comprehension.
-
Real-World Application: Actively apply your knowledge of fractions, decimals, and percentages in your daily life. Pay attention to how these concepts are used in various situations to enhance your practical understanding.
Frequently Asked Questions (FAQ)
Q: How do I simplify a fraction?
A: To simplify a fraction, find the greatest common divisor (GCD) of the numerator and the denominator. Divide both the numerator and denominator by the GCD. For example, to simplify 12/18, the GCD is 6. Dividing both by 6 gives 2/3.
Q: What if I need a more precise decimal representation of 15/58?
A: You can use a calculator or a computer program to calculate the decimal representation to many decimal places. However, remember that it will still be a non-terminating, repeating decimal.
Q: How do I convert a decimal to a percentage?
A: Multiply the decimal by 100%. For example, 0.75 multiplied by 100% equals 75%.
Q: How do I convert a percentage to a decimal?
A: Divide the percentage by 100. For example, 25% divided by 100 equals 0.25.
Q: Are there any other ways to represent 15 out of 58 besides a fraction, decimal, and percentage?
A: You could represent it visually using a pie chart or bar graph, showing 15 parts out of a total of 58 parts.
Conclusion: Mastering Proportional Reasoning
Understanding "what is 15 of 58" goes far beyond a simple numerical calculation. It's about grasping the fundamental concepts of fractions, decimals, percentages, and proportional reasoning. This understanding is essential for various mathematical applications and real-world problem-solving. By mastering these concepts and practicing regularly, you can build a strong foundation in mathematics and confidently tackle similar problems in various contexts. Remember that consistent practice and a proactive approach to learning are key to mastering these important mathematical skills.
Latest Posts
Latest Posts
-
Rewrite 17777 As A Fraction
Sep 23, 2025
-
3 2 Divided By 3
Sep 23, 2025
-
8 22 As A Percentage
Sep 23, 2025
-
Gcf Of 4 And 6
Sep 23, 2025
-
Write 0 55 As A Fraction
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 58 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.