What Is 2/3 Times 9
horsecheck
Sep 24, 2025 · 6 min read
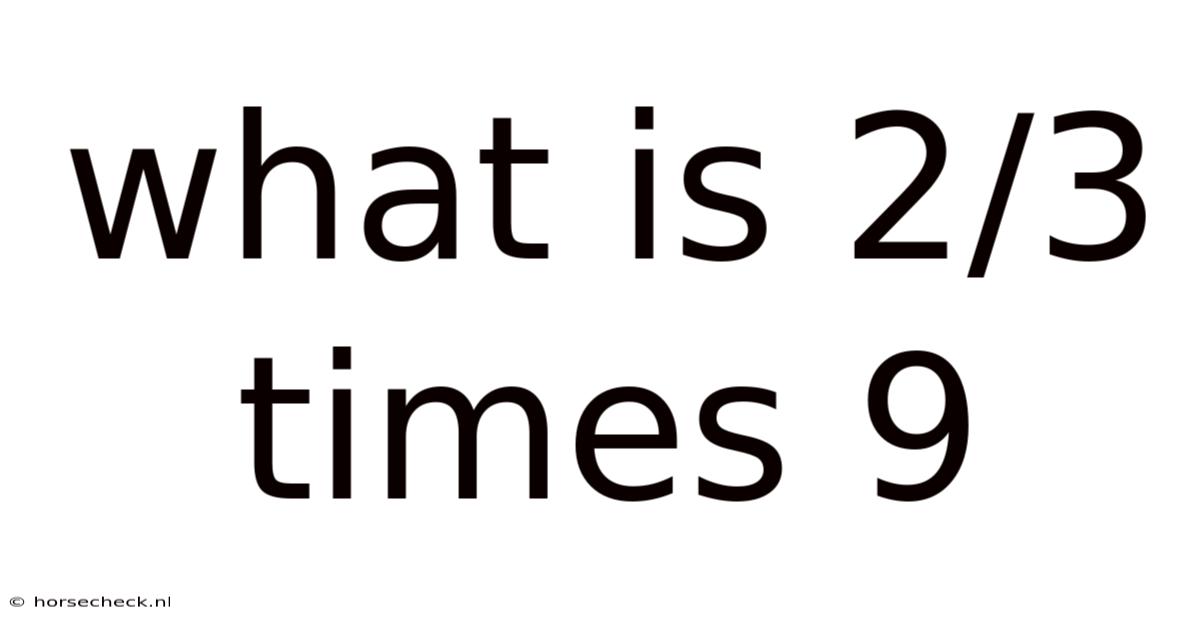
Table of Contents
What is 2/3 Times 9? Unpacking Multiplication with Fractions
This seemingly simple question, "What is 2/3 times 9?", opens a door to a deeper understanding of fraction multiplication. It's a fundamental concept in mathematics, crucial for various applications from baking to advanced engineering. This article will not only provide the answer but also delve into the 'why' behind the calculation, exploring different methods and illuminating the underlying principles. We'll even tackle some common misconceptions and frequently asked questions. By the end, you'll be equipped to confidently tackle similar problems and have a firmer grasp on fraction arithmetic.
Understanding the Basics: Fractions and Multiplication
Before diving into the specifics of 2/3 times 9, let's refresh our understanding of fractions and multiplication. A fraction represents a part of a whole. The top number, called the numerator, indicates how many parts we have, while the bottom number, the denominator, shows the total number of equal parts the whole is divided into. For example, in the fraction 2/3, the numerator is 2, and the denominator is 3. This means we have 2 parts out of a total of 3 equal parts.
Multiplication, in its simplest form, is repeated addition. When we say 2 times 3 (or 2 x 3), it means we're adding 2 three times: 2 + 2 + 2 = 6. However, when we introduce fractions, the concept of repeated addition becomes slightly more nuanced.
Method 1: Converting to an Improper Fraction
One way to solve 2/3 times 9 is by converting the whole number 9 into a fraction. Any whole number can be expressed as a fraction with a denominator of 1. Therefore, 9 can be written as 9/1. Now our problem becomes:
(2/3) x (9/1)
To multiply fractions, we simply multiply the numerators together and the denominators together:
(2 x 9) / (3 x 1) = 18/3
Now we simplify the resulting fraction. 18 divided by 3 equals 6. Therefore:
2/3 x 9 = 6
This method provides a clear, step-by-step approach, making it easy to follow and understand. It’s particularly helpful for beginners who are still grasping the concept of fraction multiplication.
Method 2: Using the Concept of "Of"
Another way to interpret "2/3 times 9" is to think of it as "2/3 of 9". This phrasing might be more intuitive for some. "Of" in this context signifies multiplication. We want to find two-thirds of nine.
Imagine we have 9 objects, like apples. To find 2/3 of these apples, we first divide the apples into three equal groups: 9 apples / 3 groups = 3 apples per group.
Since we want two-thirds, we take two of these groups: 2 groups x 3 apples/group = 6 apples.
Therefore, 2/3 of 9 is 6.
Method 3: Cancellation (Simplifying Before Multiplication)
This method utilizes the principle of cancellation, a simplification technique that makes the multiplication easier. Before multiplying the numerators and denominators directly, we can cancel out common factors between the numerator of one fraction and the denominator of the other.
In our problem, (2/3) x (9/1), we observe that 3 (the denominator of 2/3) and 9 (the numerator of 9/1) share a common factor of 3. We can simplify:
(2/3) x (9/1) = (2/1) x (3/1) = 6
We divided both 3 and 9 by their greatest common divisor, 3. This simplifies the calculation considerably, eliminating the need to work with larger numbers. This method is particularly efficient when dealing with larger fractions and more complex multiplications.
The Significance of Understanding Fraction Multiplication
The ability to multiply fractions is not just a mathematical skill; it's a foundational element for understanding a wide range of concepts and applications. Here are a few examples:
-
Cooking and Baking: Recipes often require fractional measurements. Understanding fraction multiplication is essential for accurately scaling recipes up or down. For instance, if a recipe calls for 1/2 cup of flour and you want to double the recipe, you need to calculate 2 x (1/2), resulting in 1 cup of flour.
-
Construction and Engineering: Precise measurements are crucial in construction and engineering. Calculations involving fractions are common in determining dimensions, materials, and other aspects of a project.
-
Data Analysis: Many fields, including statistics and data science, rely heavily on fractions and percentages. Understanding fraction multiplication is essential for interpreting data and drawing meaningful conclusions.
-
Finance: Interest rates, discounts, and other financial calculations often involve fractions and percentages. A strong grasp of fraction multiplication is necessary for managing personal finances and making informed financial decisions.
-
Everyday Life: From dividing a pizza among friends to understanding discounts in a store, understanding fractions is surprisingly useful in daily life.
Common Misconceptions about Fraction Multiplication
Several common misconceptions can hinder understanding fraction multiplication. Let's address a few:
-
Adding instead of multiplying: A frequent error is adding the numerators and denominators instead of multiplying them. Remember, fraction multiplication involves multiplying the numerators and multiplying the denominators separately.
-
Forgetting to simplify: After multiplying the fractions, it's crucial to simplify the resulting fraction to its lowest terms. This makes the answer clearer and easier to understand.
-
Difficulty with whole numbers: Students often struggle when incorporating whole numbers into fraction multiplication. Remember, any whole number can be written as a fraction with a denominator of 1.
Frequently Asked Questions (FAQ)
Q: Can I multiply fractions in any order?
A: Yes, multiplication of fractions is commutative. This means that the order in which you multiply the fractions does not affect the final result. (2/3) x (9/1) is the same as (9/1) x (2/3).
Q: What if the fractions are more complex?
A: The same principles apply. Multiply the numerators, multiply the denominators, and then simplify the resulting fraction. Cancellation (simplifying before multiplying) can also be used to make the calculation easier.
Q: How do I multiply mixed numbers (whole numbers and fractions)?
A: First, convert the mixed numbers into improper fractions. Then, follow the standard procedure for multiplying fractions. For example, 1 1/2 x 2/3 would first become (3/2) x (2/3) and then be simplified.
Q: What if the result is an improper fraction?
A: An improper fraction (where the numerator is larger than the denominator) can be converted into a mixed number. For example, 18/3 can be converted to 6.
Q: Are there any online tools or calculators to help with fraction multiplication?
A: Yes, many online resources and calculators are available to assist with fraction multiplication and other mathematical calculations. However, understanding the underlying principles remains crucial.
Conclusion: Mastering Fractions for a Brighter Future
The answer to "What is 2/3 times 9?" is 6. However, the true value of this exercise lies in the process of arriving at the answer. Understanding the various methods—converting to improper fractions, using the concept of "of," and employing cancellation—provides a comprehensive understanding of fraction multiplication. This fundamental skill is applicable across numerous disciplines and daily life situations. By grasping these principles, you equip yourself not just with a mathematical solution but with a broader ability to solve problems and tackle challenges that require fractional calculations. Remember to practice regularly to reinforce your understanding and build confidence in your mathematical abilities. The more you practice, the more intuitive and effortless fraction multiplication will become.
Latest Posts
Latest Posts
-
31 Out Of 36 Percentage
Sep 24, 2025
-
12 Degrees F To C
Sep 24, 2025
-
Half Of 2 3 4
Sep 24, 2025
-
Whats 15 Percent Of 30
Sep 24, 2025
-
Gcf Of 15 And 8
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 Times 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.