What Is 20 Of 44
horsecheck
Sep 24, 2025 · 5 min read
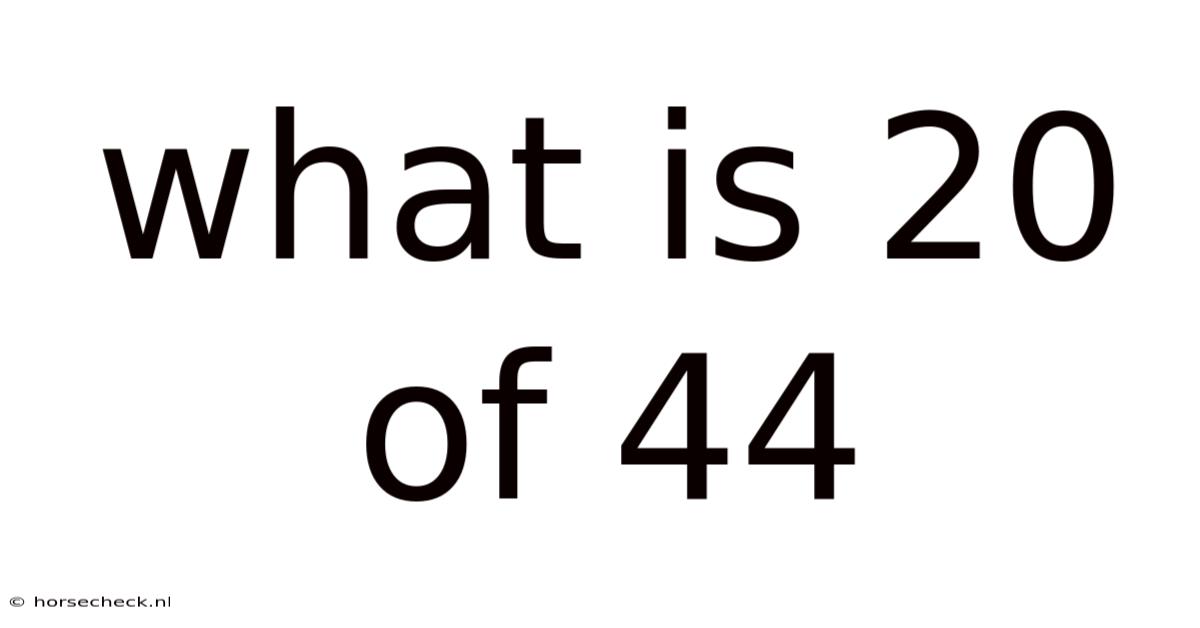
Table of Contents
What is 20 of 44? Understanding Fractions, Percentages, and Ratios
This article explores the seemingly simple question, "What is 20 of 44?" But instead of simply providing the answer (which is 20/44, or approximately 45.45%), we'll delve into the underlying mathematical concepts, explore different ways to represent this relationship, and uncover the practical applications of understanding fractions, percentages, and ratios. This comprehensive guide will equip you with the tools to tackle similar problems with confidence and a deeper understanding of fundamental mathematical principles.
Introduction: Fractions, Percentages, and Ratios - The Building Blocks
The question "What is 20 of 44?" fundamentally deals with expressing a part in relation to a whole. We can express this relationship using three key mathematical tools:
-
Fractions: Fractions represent a part of a whole, expressed as a numerator (the part) over a denominator (the whole). In our case, 20 of 44 is represented as the fraction 20/44.
-
Percentages: Percentages express a part of a whole as a fraction of 100. They're often used to represent proportions in a more easily understandable way. We'll calculate the percentage equivalent of 20/44.
-
Ratios: Ratios compare two quantities. The ratio of 20 to 44 can be written as 20:44 or 20/44. Ratios can be simplified to their lowest terms.
Understanding these concepts is crucial for solving the problem and for many real-world applications, from calculating discounts to understanding statistical data.
Calculating the Fraction: Simplifying 20/44
The fraction 20/44 represents 20 parts out of a total of 44 parts. To simplify this fraction, we need to find the greatest common divisor (GCD) of both the numerator (20) and the denominator (44). The GCD is the largest number that divides both numbers without leaving a remainder.
The factors of 20 are 1, 2, 4, 5, 10, and 20. The factors of 44 are 1, 2, 4, 11, 22, and 44.
The greatest common factor of 20 and 44 is 4. Therefore, we can simplify the fraction by dividing both the numerator and the denominator by 4:
20 ÷ 4 = 5 44 ÷ 4 = 11
So, the simplified fraction is 5/11. This means that 20 out of 44 is equivalent to 5 out of 11.
Converting the Fraction to a Percentage
To convert the fraction 5/11 (or the original 20/44) to a percentage, we need to express it as a fraction of 100. We can do this by dividing the numerator by the denominator and multiplying by 100:
(5 ÷ 11) x 100 ≈ 45.45%
Therefore, 20 out of 44 represents approximately 45.45%. This means that 20 is approximately 45.45% of 44.
Understanding Ratios: The Relationship Between 20 and 44
A ratio shows the relative size of two or more values. The ratio of 20 to 44 can be written as 20:44. Like fractions, ratios can be simplified. Since the GCD of 20 and 44 is 4, we can simplify the ratio:
20 ÷ 4 : 44 ÷ 4 = 5 : 11
The simplified ratio is 5:11. This means that for every 5 parts of one quantity, there are 11 parts of the other quantity. This simplified ratio maintains the same proportional relationship as the original ratio 20:44.
Real-World Applications: Why This Matters
Understanding fractions, percentages, and ratios is crucial in various real-world scenarios:
-
Financial Calculations: Calculating discounts, interest rates, profit margins, and tax rates all rely on these concepts. For example, if a product costs $44 and you get a 20/44 (45.45%) discount, you'll save $20.
-
Data Analysis: Understanding proportions and percentages is essential for interpreting statistical data, such as survey results, market research, and scientific findings.
-
Recipe Scaling: Adjusting recipes to serve more or fewer people involves understanding ratios. If a recipe calls for 20 grams of flour and 44 grams of sugar, you can easily scale it up or down while maintaining the correct proportions.
-
Probability and Statistics: Calculating probabilities and understanding statistical distributions often involves working with fractions and percentages.
-
Measurement and Conversions: Converting between different units of measurement, like meters to centimeters or pounds to kilograms, involves understanding ratios and proportions.
Advanced Concepts: Proportions and Problem Solving
The concept of proportion is closely related to fractions and ratios. A proportion states that two ratios are equal. We can use proportions to solve problems where we know some parts of a relationship and need to find the others. For instance:
If 20 out of 44 people surveyed prefer a certain product, and we survey 100 people, how many would we expect to prefer the same product?
We can set up a proportion:
20/44 = x/100
To solve for x (the number of people out of 100 who prefer the product), we cross-multiply:
20 * 100 = 44 * x 2000 = 44x x = 2000/44 ≈ 45.45
We would expect approximately 45 people out of 100 to prefer the product.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this? A: Yes, a calculator can help with the division and percentage calculations, but understanding the underlying concepts of fractions, percentages, and ratios is essential.
-
Q: Are there other ways to represent 20 of 44? A: Yes, you could use decimals (0.4545), a simplified ratio (5:11), or a description like "five elevenths."
-
Q: What if I have a different problem with different numbers? A: The same principles apply. Identify the part and the whole, create a fraction, simplify it if possible, convert it to a percentage if needed, and use ratios to understand the proportional relationship.
-
Q: Why is it important to simplify fractions? A: Simplifying fractions makes them easier to work with and understand. It also helps in comparing fractions more effectively.
Conclusion: Mastering the Fundamentals
The question "What is 20 of 44?" might seem straightforward, but it opens a door to a broader understanding of fundamental mathematical concepts—fractions, percentages, and ratios. These concepts are not just abstract mathematical ideas; they are tools that empower us to analyze data, solve problems, and navigate a world filled with numerical relationships. Mastering these fundamentals is essential for success in various fields, from finance and science to everyday life decision-making. By understanding these concepts, you're not only answering a simple question but developing essential mathematical literacy that will benefit you in countless ways. Remember to always simplify your fractions and ratios for easier interpretation and problem-solving.
Latest Posts
Latest Posts
-
Lcm Of 8 4 2
Sep 24, 2025
-
Multiples Of 12 And 15
Sep 24, 2025
-
Gcf Of 12 And 3
Sep 24, 2025
-
Is 34 A Perfect Square
Sep 24, 2025
-
What Is 100 Of 20
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 44 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.