What Is 20 Of $9
horsecheck
Sep 23, 2025 · 5 min read
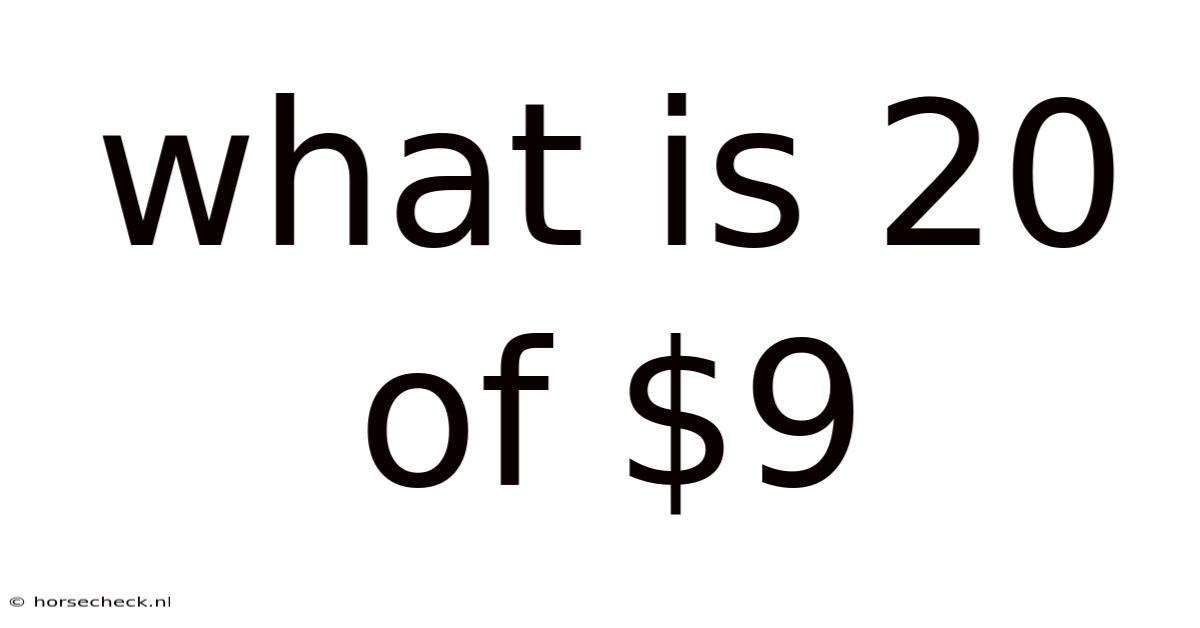
Table of Contents
What is 20% of $9? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and taxes to comprehending statistical data and financial reports. This article will thoroughly explore the question "What is 20% of $9?" We'll not only solve this specific problem but also delve into the underlying principles of percentage calculations, providing you with a comprehensive understanding and equipping you with the tools to tackle similar problems independently. This exploration will touch upon different calculation methods, practical applications, and address frequently asked questions.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" ("per cent"). Therefore, 20% means 20 out of 100, which can be represented as the fraction 20/100 or the decimal 0.20. Understanding this fundamental concept is crucial for all percentage calculations.
Calculating 20% of $9: Method 1 - Using Decimal Conversion
The most straightforward method involves converting the percentage to a decimal and then multiplying it by the original amount. To find 20% of $9, we follow these steps:
- Convert the percentage to a decimal: 20% = 20/100 = 0.20
- Multiply the decimal by the original amount: 0.20 * $9 = $1.80
Therefore, 20% of $9 is $\boxed{$1.80}$.
Calculating 20% of $9: Method 2 - Using Fraction Conversion
Alternatively, we can use the fraction representation of the percentage.
- Convert the percentage to a fraction: 20% = 20/100
- Simplify the fraction (if possible): 20/100 simplifies to 1/5
- Multiply the fraction by the original amount: (1/5) * $9 = $9/5 = $1.80
This method reinforces the concept of percentages as fractions and provides a different perspective on the calculation. Again, we arrive at the answer: 20% of $9 is $\boxed{$1.80}$.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world scenarios:
-
Shopping and Sales: Calculating discounts during sales is a common application. For example, a 20% discount on a $9 item saves you $1.80.
-
Taxes: Understanding sales tax percentages allows you to determine the final price of an item, including the tax. If the sales tax is 6%, you would calculate 6% of the price and add it to the original amount.
-
Tips and Gratuities: Calculating a tip at a restaurant often involves determining a percentage of the total bill.
-
Financial Investments: Percentage changes in investment values are frequently used to track performance and growth.
-
Statistical Analysis: Percentages are crucial for representing and interpreting data in various fields, including demographics, economics, and science.
-
Grade Calculations: In academic settings, percentages are used to express grades and overall performance.
Beyond the Basics: Understanding Percentage Increase and Decrease
While finding a percentage of a number is fundamental, understanding percentage increase and decrease is equally important. Let's explore these concepts further.
Percentage Increase: This involves calculating the amount by which a value has increased relative to its original value. The formula is:
Percentage Increase = [(New Value - Original Value) / Original Value] * 100%
For instance, if a price increases from $9 to $10, the percentage increase is:
[(10 - 9) / 9] * 100% = 11.11% (approximately)
Percentage Decrease: This mirrors the concept of percentage increase, but it's used when a value decreases. The formula is:
Percentage Decrease = [(Original Value - New Value) / Original Value] * 100%
If the price of a $9 item decreases to $7, the percentage decrease is:
[(9 - 7) / 9] * 100% = 22.22% (approximately)
Advanced Applications: Compound Interest and Growth
Percentage calculations become even more complex and significant when dealing with compounding effects. Compound interest, for instance, involves earning interest not only on the principal amount but also on accumulated interest. This leads to exponential growth over time. The formula for compound interest is:
A = P (1 + r/n)^(nt)
Where:
- A = the future value of the investment/loan, including interest
- P = the principal investment amount (the initial deposit or loan amount)
- r = the annual interest rate (decimal)
- n = the number of times that interest is compounded per year
- t = the number of years the money is invested or borrowed for
Understanding compound interest is crucial for planning long-term investments and managing debts.
Frequently Asked Questions (FAQs)
Q1: How do I calculate a different percentage of $9?
A1: Simply replace "20%" with the desired percentage in the calculation. For example, to find 35% of $9, convert 35% to a decimal (0.35) and multiply it by $9 (0.35 * $9 = $3.15).
Q2: What if I need to find the percentage one number represents of another?
A2: Use the formula: (Part / Whole) * 100% . For example, if 3 out of 10 apples are red, the percentage of red apples is (3/10) * 100% = 30%.
Q3: How can I improve my understanding of percentages?
A3: Practice is key! Work through various percentage problems, starting with simple examples and gradually increasing the complexity. Online resources, worksheets, and interactive exercises can be beneficial.
Q4: Are there any online calculators for percentage calculations?
A4: Yes, numerous online percentage calculators are available. These can be helpful for quick calculations, but understanding the underlying principles remains crucial.
Q5: Can percentages be negative?
A5: Yes, percentages can be negative. They are used to represent decreases or negative changes in values.
Conclusion
Calculating 20% of $9, as we've shown, yields $1.80. However, this simple calculation provides a gateway to understanding the broader world of percentage applications. Mastering percentage calculations is essential for navigating various aspects of daily life, from personal finance to professional fields. By understanding the methods, practicing different scenarios, and exploring advanced applications, you can build a strong foundation in this fundamental mathematical concept. Remember to practice regularly and don't hesitate to utilize different methods to reinforce your understanding. This will ultimately empower you to confidently tackle a wide range of percentage-related problems with ease and accuracy.
Latest Posts
Latest Posts
-
What Is 15 Of 22
Sep 23, 2025
-
What Percentage Is 1 8th
Sep 23, 2025
-
Whats 19 Celsius In Fahrenheit
Sep 23, 2025
-
Lcm Of 7 And 5
Sep 23, 2025
-
149 Degrees Fahrenheit To Celsius
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of $9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.