What Is 3/4 Of 5
horsecheck
Sep 23, 2025 · 6 min read
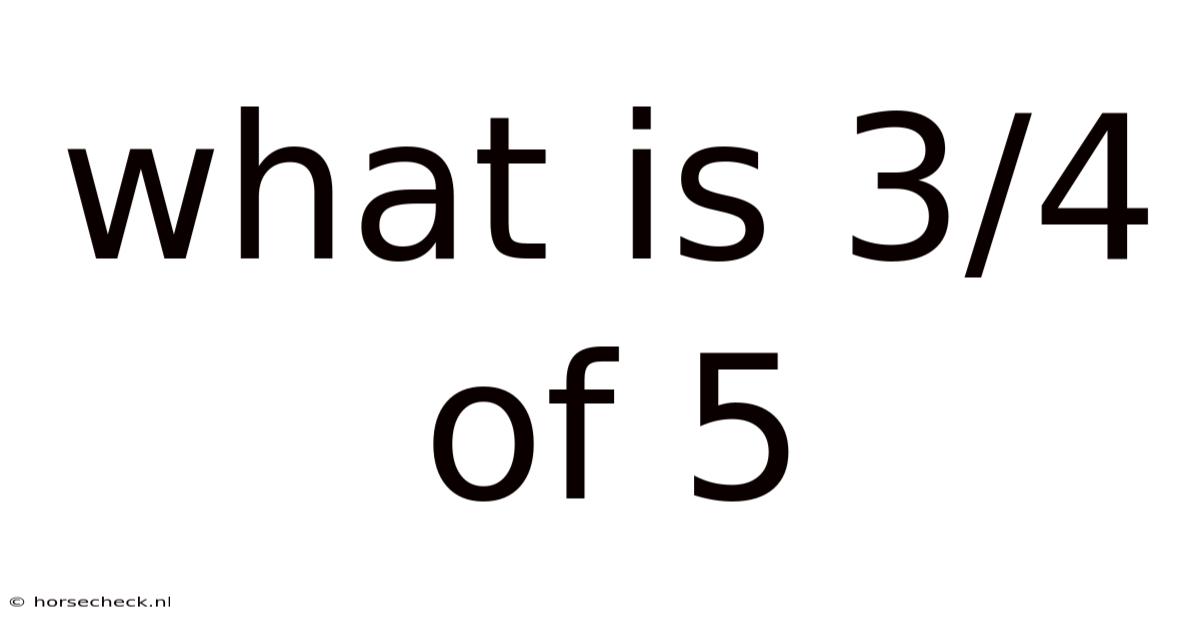
Table of Contents
What is 3/4 of 5? A Deep Dive into Fractions and Multiplication
Finding 3/4 of 5 might seem like a simple problem, suitable only for elementary school students. However, understanding how to solve this seemingly basic calculation unlocks a deeper understanding of fractions, multiplication, and their applications in everyday life. This article will not only provide the answer but will delve into the underlying mathematical principles, explore different solution methods, and discuss the broader significance of fractional calculations.
Introduction: Understanding Fractions and Multiplication
Before we tackle the specific problem of finding 3/4 of 5, let's refresh our understanding of fractions and multiplication. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered.
Multiplication, in its simplest form, is repeated addition. When we multiply two numbers, we're essentially adding one number to itself as many times as the other number indicates. For example, 3 x 5 means adding 3 to itself 5 times (3 + 3 + 3 + 3 + 3 = 15). Applying this concept to fractions introduces a crucial element: finding a portion of a whole.
Methods for Solving: 3/4 of 5
There are several ways to calculate 3/4 of 5. Each method highlights different aspects of fractional arithmetic, making it valuable to explore multiple approaches.
Method 1: Converting the Whole Number to a Fraction
This method leverages the understanding that any whole number can be expressed as a fraction with a denominator of 1. Therefore, we can rewrite 5 as 5/1. Now, we can multiply the two fractions:
(3/4) x (5/1) = (3 x 5) / (4 x 1) = 15/4
This improper fraction (where the numerator is larger than the denominator) can be converted into a mixed number. We divide the numerator (15) by the denominator (4):
15 ÷ 4 = 3 with a remainder of 3
Therefore, 15/4 is equivalent to 3 ¾. So, 3/4 of 5 is 3 ¾.
Method 2: Finding the Fraction of One Unit
This method involves finding what one-fourth (1/4) of 5 is and then multiplying that result by 3.
1/4 of 5 = 5/4 = 1 ¼
Now, multiply this result by 3:
3 x (1 ¼) = 3 + (3 x ¼) = 3 + ¾ = 3 ¾
This approach provides a clear step-by-step visualization of the problem, making it particularly helpful for beginners.
Method 3: Using Decimal Equivalents
Converting fractions to decimals can sometimes simplify calculations. The fraction 3/4 is equivalent to the decimal 0.75. We can then multiply this decimal by 5:
0.75 x 5 = 3.75
This decimal, 3.75, is equivalent to the mixed number 3 ¾. This method is particularly useful when dealing with more complex fractions or when using a calculator.
Method 4: Visual Representation
Visual aids can be extremely helpful, especially for those who struggle with abstract mathematical concepts. Imagine a rectangle representing the whole number 5. Divide this rectangle into four equal parts, representing the denominator of the fraction (4). Each part represents 1 ¼ (5 divided by 4). Now, shade in three of these four parts to represent the numerator (3). The shaded area visually represents 3/4 of 5, which is again, 3 ¾.
Expanding the Concept: Real-World Applications
Understanding how to calculate fractions of whole numbers has extensive real-world applications. Here are a few examples:
- Cooking and Baking: Many recipes require fractional measurements of ingredients. For example, a recipe might call for 3/4 cup of sugar.
- Construction and Engineering: Precise measurements are critical in construction and engineering. Fractions are essential for accurate calculations in areas like cutting materials or designing structures.
- Finance and Budgeting: Fractions are used to represent percentages and proportions in financial calculations, such as calculating interest rates, discounts, or taxes.
- Data Analysis: Understanding fractions is crucial when interpreting statistical data represented as proportions or percentages.
Explanation of the Mathematical Principles Involved
The core mathematical principle at play here is the concept of multiplication of fractions. When multiplying fractions, we multiply the numerators together to obtain the new numerator and the denominators together to obtain the new denominator. This is formalized as:
(a/b) x (c/d) = (a x c) / (b x d)
This principle applies to all fraction multiplications, including those involving whole numbers (which, as we've seen, can be expressed as fractions with a denominator of 1). Understanding this principle is fundamental to mastering more complex fractional calculations.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this problem? A: Yes, you can. You can either input the fraction directly (if your calculator allows it) or convert the fraction to a decimal (0.75) and multiply by 5.
-
Q: What if the fraction was different? How would the process change? A: The process remains the same. You would still multiply the fraction by the whole number, converting to a mixed number if necessary. For example, to find 2/3 of 5, you would calculate (2/3) x (5/1) = 10/3 = 3 ⅓.
-
Q: Why are there multiple ways to solve this problem? A: Different methods highlight different aspects of the underlying mathematical principles. Some methods might be easier to grasp than others, depending on your individual learning style and prior mathematical knowledge.
-
Q: Is there a way to simplify the calculation before multiplying? A: Not in this particular case, as 3 and 4 share no common factors with 5. However, in other problems, you could simplify the fractions before multiplying to make the calculation easier. This involves finding the greatest common divisor (GCD) of the numbers and dividing both the numerator and denominator by it.
Conclusion: Mastering Fractions – A Foundation for Future Learning
Finding 3/4 of 5, while a seemingly simple problem, provides a robust foundation for understanding crucial mathematical concepts. Mastering fractional calculations is not just about getting the right answer; it’s about cultivating a deeper understanding of mathematical principles, building problem-solving skills, and developing the ability to apply these concepts in various real-world scenarios. The different methods explored in this article highlight the versatility of mathematical approaches and encourage a deeper exploration of the subject. The ability to perform these seemingly simple calculations proficiently will serve as a building block for more complex mathematical endeavors in the future. So, remember, 3/4 of 5 is 3 ¾, but the journey to understanding how to get there is far more valuable than the answer itself.
Latest Posts
Latest Posts
-
Is 207 A Prime Number
Sep 24, 2025
-
What Is A 12 20
Sep 24, 2025
-
Square Root Of 162 Simplified
Sep 24, 2025
-
108 Grados Fahrenheit A Celsius
Sep 24, 2025
-
3 5 Is What Percent
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 3/4 Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.