What Is 30 Of 9
horsecheck
Sep 23, 2025 · 5 min read
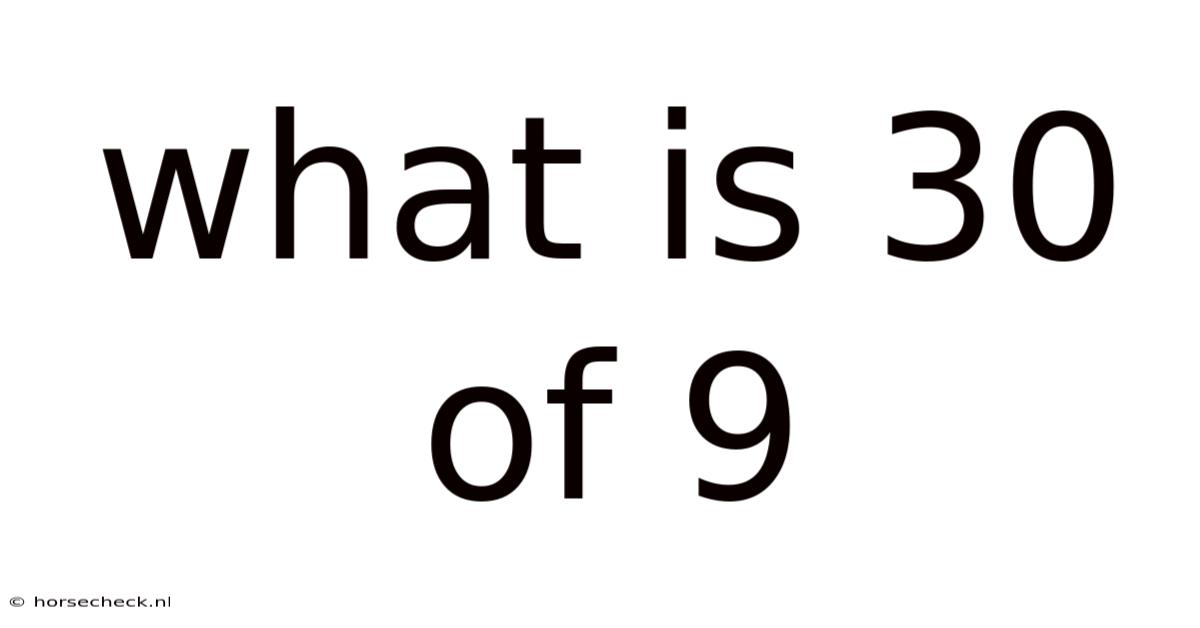
Table of Contents
What is 30% of 9? A Comprehensive Guide to Percentages and their Applications
Understanding percentages is a fundamental skill applicable across numerous areas of life, from calculating discounts at the mall to analyzing financial reports. This article delves into the calculation of 30% of 9, providing a step-by-step explanation, exploring the underlying mathematical principles, and expanding on the broader applications of percentages in various contexts. This guide aims to not only answer the immediate question but also equip you with the tools to tackle similar percentage problems with confidence.
Understanding Percentages: A Foundation
A percentage is a fraction or a ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred" (from the Latin per centum). We represent percentages using the "%" symbol. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5 as a decimal.
This fundamental understanding is crucial for calculating any percentage, including finding 30% of 9.
Calculating 30% of 9: Step-by-Step
There are several ways to calculate 30% of 9. Let's explore the most common and straightforward methods:
Method 1: Converting the Percentage to a Decimal
-
Convert the percentage to a decimal: To convert 30% to a decimal, divide it by 100: 30% / 100 = 0.30 or 0.3
-
Multiply the decimal by the number: Multiply the decimal (0.3) by the number you want to find the percentage of (9): 0.3 * 9 = 2.7
Therefore, 30% of 9 is 2.7
Method 2: Using Fractions
-
Convert the percentage to a fraction: 30% can be expressed as the fraction 30/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor (10): 30/100 = 3/10
-
Multiply the fraction by the number: Multiply the simplified fraction (3/10) by the number (9): (3/10) * 9 = 27/10
-
Convert the improper fraction to a decimal: Convert the improper fraction 27/10 to a decimal by dividing the numerator by the denominator: 27/10 = 2.7
Therefore, 30% of 9 is 2.7
Why these methods work: A deeper mathematical explanation
Both methods rely on the core definition of a percentage as a fraction of 100. When we convert a percentage to a decimal, we're essentially expressing the percentage as a fraction with a denominator of 1. Multiplying this decimal by the given number performs the same operation as multiplying the original fraction (representing the percentage) by the number.
For example, using the fraction method, we have (30/100) * 9. This calculation represents taking 30 parts out of 100 of the number 9. Simplifying the fraction and then multiplying streamlines the process while maintaining mathematical accuracy.
Practical Applications of Percentages: Beyond the Classroom
Understanding percentages isn't just an academic exercise; it’s a crucial life skill with applications across many domains:
-
Retail and Sales: Calculating discounts, sales tax, and profit margins are all based on percentage calculations. If a store offers a 30% discount on an item priced at $9, you would use the same method described above to find the discount amount ($2.70) and the final price ($6.30).
-
Finance: Interest rates on loans and savings accounts are expressed as percentages. Calculating compound interest, understanding APR (Annual Percentage Rate), and analyzing investment returns all involve percentage calculations.
-
Data Analysis and Statistics: Percentages are fundamental to representing and interpreting data. For example, expressing survey results, market share, or changes in population as percentages allows for easy comparison and understanding.
-
Scientific Research: Many scientific studies use percentages to express data, such as the percentage of a population affected by a disease, or the percentage change in a measured variable after an experiment.
-
Everyday Life: From figuring out tips in restaurants (e.g., 15% of the bill) to understanding nutritional information on food labels (e.g., percentage of daily value for nutrients), percentages are integrated into many aspects of daily life.
Expanding the Scope: Calculating Other Percentages
Mastering the calculation of 30% of 9 provides a solid foundation for tackling more complex percentage problems. The same principles and methods apply, regardless of the percentage or the number. For instance, let's consider a few examples:
-
Finding 15% of 25:
- Convert 15% to a decimal: 15% / 100 = 0.15
- Multiply the decimal by 25: 0.15 * 25 = 3.75
-
Finding 75% of 60:
- Convert 75% to a fraction: 75/100 = 3/4
- Multiply the fraction by 60: (3/4) * 60 = 45
-
Finding x% of y:
The general formula is: (x/100) * y where x represents the percentage and y represents the number.
Frequently Asked Questions (FAQ)
Q1: What if I need to find a percentage of a number that results in a fraction?
A1: There's nothing wrong with getting a fractional answer when calculating a percentage. Percentages can and often do result in fractional or decimal values, reflecting a part of a whole. For instance, 25% of 7 is 1.75.
Q2: Are there any shortcuts for calculating percentages mentally?
A2: Yes, for certain percentages, mental shortcuts can be helpful. For example, 10% of a number is simply that number divided by 10. 5% is half of 10%, and 20% is double 10%. These shortcuts can be helpful, especially with simpler calculations. Practice is key to mastering them.
Q3: How can I improve my understanding of percentages?
A3: Practice is the best way to improve your understanding of percentages. Work through different examples, using both the decimal and fraction methods. Try to solve percentage problems in different contexts, like those described in the “Practical Applications” section. You can find many online resources and worksheets to help you practice.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 30% of 9, as demonstrated above, is not just about finding the answer (2.7). It’s about understanding the fundamental principles of percentages and their wide-ranging applications in various fields. This ability is vital for making informed decisions in personal finance, career pursuits, and many other aspects of life. By grasping these concepts and practicing regularly, you equip yourself with a powerful tool for navigating a data-driven world. Remember that the key to mastering percentages lies in consistent practice and understanding the underlying mathematical principles. With dedication, anyone can confidently approach and solve percentage problems, ensuring successful application in various aspects of their lives.
Latest Posts
Latest Posts
-
Factors Of 15 And 12
Sep 23, 2025
-
0 25 As A Whole Number
Sep 23, 2025
-
Convert 18 Fahrenheit To Celsius
Sep 23, 2025
-
Gcf Of 6 And 5
Sep 23, 2025
-
What Is A 8 15 Grade
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.