What Is 40 Of 22
horsecheck
Sep 25, 2025 · 6 min read
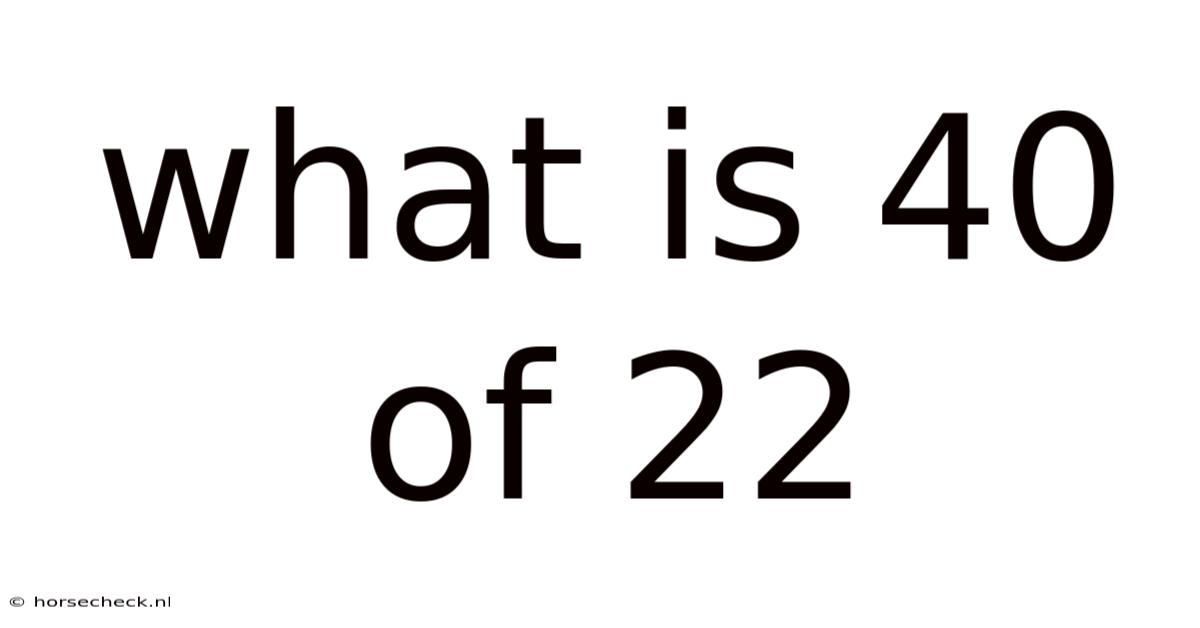
Table of Contents
What is 40% of 22? A Deep Dive into Percentages and Practical Applications
Finding 40% of 22 might seem like a simple calculation, but it opens a door to understanding a fundamental mathematical concept: percentages. This seemingly basic question allows us to explore different methods of calculation, delve into the underlying principles, and discover the widespread applications of percentages in everyday life. This article will not only answer the question directly but also provide a comprehensive understanding of percentage calculations and their relevance in various fields.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 40% can be written as 40/100, or its simplified fraction, 2/5. This means that 40% represents 40 parts out of a total of 100 parts.
Understanding this fundamental concept is crucial before tackling any percentage problem. It allows you to visualize the portion you're trying to calculate and grasp the relationship between the percentage, the whole, and the part.
Method 1: Converting Percentage to Decimal
This is arguably the most straightforward method. We convert the percentage into a decimal and then multiply it by the number.
-
Step 1: Convert the percentage to a decimal. To do this, divide the percentage by 100. In this case, 40% becomes 40 ÷ 100 = 0.40 or 0.4.
-
Step 2: Multiply the decimal by the number. Multiply 0.4 by 22: 0.4 x 22 = 8.8
Therefore, 40% of 22 is 8.8.
Method 2: Using Fractions
This method utilizes the fractional representation of the percentage.
-
Step 1: Express the percentage as a fraction. As mentioned earlier, 40% is equivalent to 40/100, which simplifies to 2/5.
-
Step 2: Multiply the fraction by the number. Multiply 2/5 by 22: (2/5) x 22 = 44/5
-
Step 3: Convert the improper fraction to a decimal. Divide 44 by 5: 44 ÷ 5 = 8.8
Again, we arrive at the answer: 40% of 22 is 8.8.
Method 3: Proportion Method
This method uses the concept of ratios and proportions to solve the problem.
-
Step 1: Set up a proportion. We can set up a proportion as follows:
40/100 = x/22
Where 'x' represents the unknown value (40% of 22).
-
Step 2: Cross-multiply. Cross-multiplying gives us:
100x = 40 x 22
-
Step 3: Solve for x. Solving for 'x':
100x = 880 x = 880 ÷ 100 x = 8.8
Once more, we confirm that 40% of 22 is 8.8.
Choosing the Best Method
Each method provides the same accurate result. The best method for you depends on your preference and the complexity of the problem. The decimal method is often the quickest and most efficient for simple calculations like this one. The fraction method is useful for developing a deeper understanding of the underlying mathematical principles. The proportion method is particularly helpful when dealing with more complex percentage problems or when setting up a visual representation of the problem.
Beyond the Calculation: Real-World Applications
The ability to calculate percentages is essential in many real-world situations. Here are a few examples:
-
Sales and Discounts: Stores frequently offer discounts expressed as percentages. Understanding percentage calculations allows you to quickly determine the final price after a discount. For instance, a 40% discount on a $22 item would result in a saving of $8.80.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Calculating these taxes requires an understanding of percentage calculations.
-
Tips and Gratuities: Calculating a tip in a restaurant often involves determining a percentage of the total bill.
-
Interest Rates: Interest earned on savings accounts or paid on loans is typically expressed as an annual percentage rate (APR).
-
Statistics and Data Analysis: Percentages are fundamental in analyzing and presenting statistical data. They allow for easy comparison and interpretation of different data sets. For example, understanding the percentage change in a company's profits year-over-year is crucial for investors.
-
Financial Planning: Budgeting, investment strategies, and retirement planning all rely heavily on percentage calculations.
-
Science and Engineering: Percentages are used extensively in scientific experiments and engineering calculations to express quantities relative to a whole. For example, expressing the concentration of a solution as a percentage.
Dealing with More Complex Percentage Problems
While the example of calculating 40% of 22 is relatively straightforward, percentage problems can become more complex. Here are some examples and how to approach them:
-
Finding the percentage: If you know the part and the whole, you can find the percentage by dividing the part by the whole and multiplying by 100. For example, what percentage of 22 is 8.8? (8.8 ÷ 22) x 100 = 40%
-
Finding the whole: If you know the part and the percentage, you can find the whole by dividing the part by the percentage (expressed as a decimal). For example, if 40% of a number is 8.8, what is the number? 8.8 ÷ 0.4 = 22
-
Percentage increase or decrease: These calculations involve finding the difference between two values and expressing it as a percentage of the original value.
-
Compound interest: This involves calculating interest on both the principal amount and accumulated interest. This requires repeated percentage calculations.
Frequently Asked Questions (FAQ)
-
Q: What if the percentage is not a whole number, such as 37.5%?
A: You can use the same methods outlined above, simply converting the percentage to its decimal equivalent (37.5% = 0.375) and performing the multiplication.
-
Q: How can I calculate percentages quickly without a calculator?
A: For some percentages, mental math tricks can be helpful. For example, 10% of a number is easily found by moving the decimal point one place to the left. Other percentages can be broken down into simpler percentages (e.g., 15% = 10% + 5%).
-
Q: Are there online calculators or software for percentage calculations?
A: Yes, numerous online calculators and spreadsheet software (like Microsoft Excel or Google Sheets) offer built-in functions for performing percentage calculations quickly and accurately.
Conclusion
Calculating 40% of 22, resulting in 8.8, is just the starting point for understanding the power and versatility of percentages. From everyday shopping to complex financial modeling, the ability to work confidently with percentages is an invaluable skill. This article has not only provided different methods to solve this specific problem but also laid a foundation for tackling a wide range of percentage-related calculations. Mastering these methods will empower you to navigate numerous situations in your personal and professional life where understanding percentages is crucial. Remember to choose the method that feels most comfortable and efficient for you, and practice regularly to build your confidence and proficiency.
Latest Posts
Latest Posts
-
Whats 85 As A Fraction
Sep 25, 2025
-
7 50 As A Decimal
Sep 25, 2025
-
Square Root Of 92 Simplified
Sep 25, 2025
-
What Is 1000 Times 1000
Sep 25, 2025
-
Whats 11 Out Of 15
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 22 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.