What Is 45 Of 90
horsecheck
Sep 22, 2025 · 6 min read
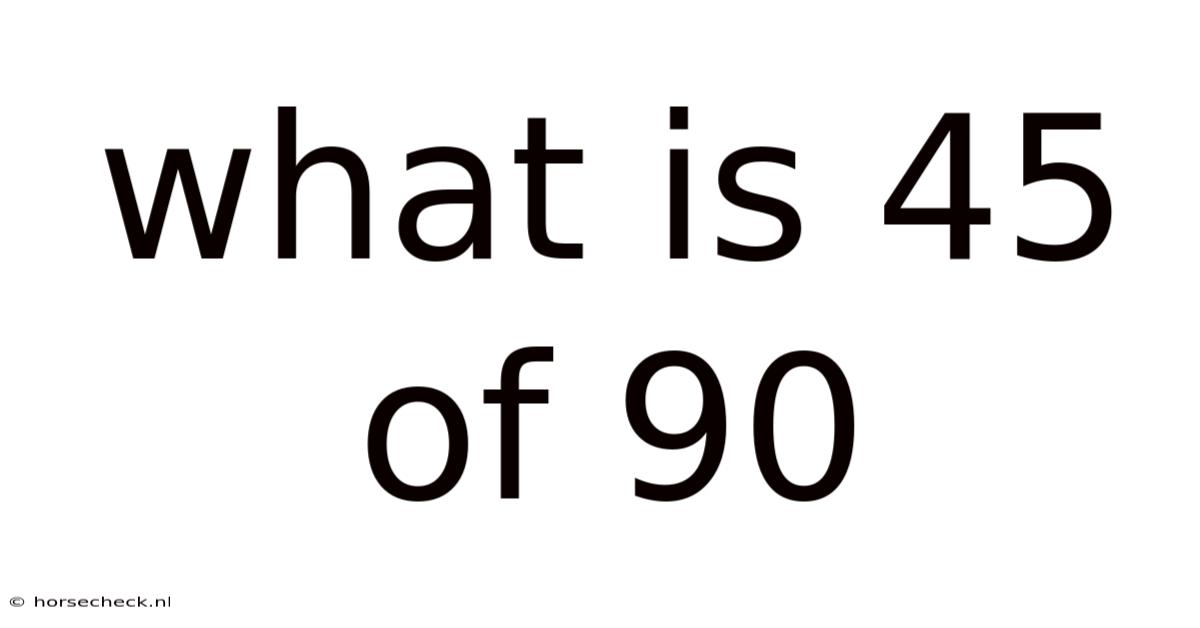
Table of Contents
What is 45 of 90? Unveiling the World of Fractions, Percentages, and Ratios
This article delves into the seemingly simple question: "What is 45 of 90?" While the immediate answer might seem obvious, this question opens a door to a fascinating exploration of fundamental mathematical concepts like fractions, percentages, and ratios. Understanding these concepts is crucial for navigating everyday life, from calculating discounts to comprehending statistical data. We'll unpack the different ways to interpret and solve this problem, highlighting the underlying principles and practical applications.
Understanding the Fundamentals: Fractions, Percentages, and Ratios
Before diving into the solution, let's establish a clear understanding of the core mathematical concepts involved:
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). For example, 1/2 represents one part out of two equal parts.
-
Percentages: A percentage is a fraction expressed as a portion of 100. The symbol "%" represents "per cent" or "out of 100". For example, 50% is equivalent to 50/100, which simplifies to 1/2.
-
Ratios: A ratio is a comparison of two or more quantities. It shows the relative size of one quantity compared to another. Ratios can be expressed in different ways: using the colon symbol (e.g., 1:2), as a fraction (e.g., 1/2), or in words (e.g., one to two).
Solving "What is 45 of 90?" – Different Approaches
The question "What is 45 of 90?" can be interpreted in several ways, leading to different solutions depending on the intended meaning. Let's explore the most common interpretations:
1. 45 as a Fraction of 90:
This interpretation asks what fraction 45 represents when compared to 90. To solve this, we express it as a fraction: 45/90.
This fraction can be simplified by finding the greatest common divisor (GCD) of 45 and 90, which is 45. Dividing both the numerator and denominator by 45, we get:
45/90 = 1/2
Therefore, 45 is one-half of 90.
2. 45 as a Percentage of 90:
This interpretation asks what percentage 45 represents out of 90. To solve this, we can use the following formula:
(Part / Whole) * 100%
In this case, the part is 45, and the whole is 90. Substituting these values into the formula, we get:
(45 / 90) * 100% = 0.5 * 100% = 50%
Therefore, 45 is 50% of 90.
3. 45 in Relation to 90 as a Ratio:
This interpretation focuses on the relative size of 45 compared to 90. The ratio can be expressed as:
45:90
Similar to the fraction, we can simplify this ratio by dividing both sides by their GCD (45):
45:90 = 1:2
This means the ratio of 45 to 90 is 1:2, indicating that 45 is half the size of 90.
Practical Applications and Real-World Examples
Understanding fractions, percentages, and ratios is vital for various real-world situations. Here are some examples where the concept of "45 of 90" and similar calculations might be applied:
-
Discounts and Sales: A store offering a 50% discount on an item priced at $90 would reduce the price by $45 (50% of $90). This is directly related to our finding that 45 is 50% of 90.
-
Test Scores: If a test has 90 questions, and a student answers 45 correctly, their score is 50% (45/90 * 100%).
-
Recipe Scaling: If a recipe calls for 90 grams of flour and you want to halve the recipe, you would use 45 grams of flour.
-
Data Analysis: In statistics, ratios and percentages are essential for interpreting data and drawing conclusions. For example, if a survey shows that 45 out of 90 respondents prefer a particular product, the result indicates a 50% preference.
-
Geometry and Measurement: Understanding fractions and ratios is crucial in geometry for calculating areas, volumes, and proportions.
Expanding the Understanding: Beyond Simple Calculations
While solving "What is 45 of 90?" provides a basic understanding of fractions, percentages, and ratios, it's important to expand this knowledge to handle more complex scenarios:
-
Working with Decimals: Often, we encounter situations where the numbers aren't whole numbers. Understanding how to work with decimals in these calculations is crucial.
-
Complex Fractions: Some problems might involve fractions within fractions (complex fractions). Learning how to simplify and solve complex fractions is an important skill.
-
Proportions: Solving proportions involves finding an unknown value in a ratio by setting up an equation. This is a highly useful skill in many fields, including science and engineering.
-
Percentage Increase and Decrease: Calculating percentage increases and decreases is important for understanding growth rates, price changes, and other dynamic situations.
Frequently Asked Questions (FAQs)
Q1: What if the numbers weren't so easily divisible?
A1: If the numbers weren't easily divisible, you'd still follow the same principles. You'd express the numbers as a fraction, simplify it as much as possible, and then convert it to a percentage if needed. A calculator can be useful for more complex calculations.
Q2: Are there other ways to solve this problem?
A2: Yes, you could also use the concept of proportions to solve this problem. You could set up a proportion like this: x/90 = 1/2 and solve for x. This would give you the same answer of 45.
Q3: Why is understanding fractions, percentages, and ratios important?
A3: These concepts form the foundation of many mathematical and real-world applications. They are essential for everything from basic arithmetic to advanced calculations in finance, science, and engineering.
Q4: What are some resources for further learning?
A4: Numerous online resources, textbooks, and educational videos are available to help you deepen your understanding of fractions, percentages, and ratios. Many websites and educational platforms offer interactive exercises and tutorials to support learning.
Conclusion: Mastering the Fundamentals
The seemingly simple question, "What is 45 of 90?" has led us on a journey exploring fundamental mathematical concepts. We've seen that the answer depends on how the question is interpreted – as a fraction, a percentage, or a ratio. Each approach highlights the importance of understanding these basic concepts and their applications in real-world situations. By mastering fractions, percentages, and ratios, you equip yourself with valuable tools for solving problems and making informed decisions in various aspects of life, from everyday tasks to complex calculations. The key takeaway is that a solid foundation in these core mathematical concepts is essential for success in many fields and empowers you to confidently tackle numerical challenges. Remember to practice regularly and explore different examples to solidify your understanding.
Latest Posts
Latest Posts
-
62 5 As A Mixed Number
Sep 22, 2025
-
33 1 3 To Decimal
Sep 22, 2025
-
98 8 Fahrenheit To Celsius
Sep 22, 2025
-
19 26 As A Percentage
Sep 22, 2025
-
2 3 Repeating As A Fraction
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 45 Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.