What Is 50 Of 26
horsecheck
Sep 23, 2025 · 5 min read
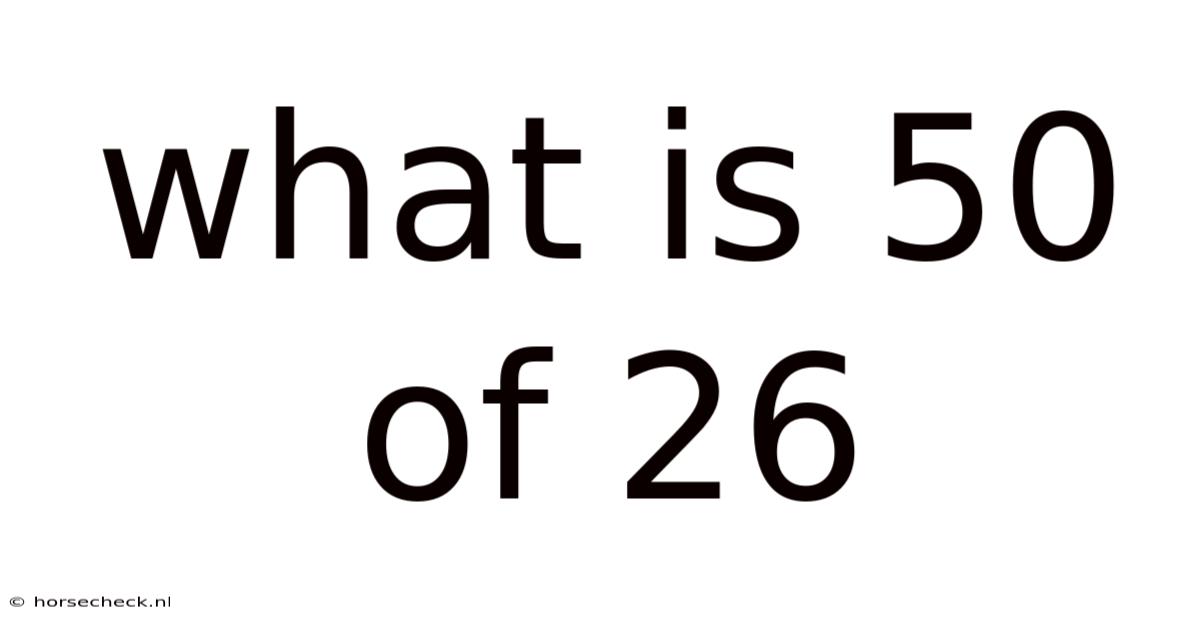
Table of Contents
What is 50% of 26? A Deep Dive into Percentages and Their Applications
Finding 50% of 26 might seem like a simple task, easily solvable with a quick calculation. However, understanding the underlying principles of percentages unlocks a world of practical applications far beyond this basic problem. This article will not only solve the problem but also explore the concept of percentages, different methods for calculating them, and demonstrate their relevance in various real-world scenarios. We'll cover everything from basic arithmetic to more advanced applications, ensuring you develop a comprehensive understanding of this fundamental mathematical concept.
Introduction: Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). So, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. This fundamental understanding is crucial for calculating percentages efficiently. Knowing that 50% represents half immediately simplifies the calculation for 50% of 26, but let's explore several ways to solve this, illustrating diverse mathematical approaches.
Method 1: Direct Calculation using Fractions
The most straightforward approach leverages the fractional representation of 50%. As mentioned earlier, 50% is equivalent to 1/2. Therefore, finding 50% of 26 is the same as finding half of 26.
This simplifies to: (1/2) * 26 = 26/2 = 13
Therefore, 50% of 26 is 13.
Method 2: Decimal Conversion
Another common method involves converting the percentage to its decimal equivalent. To do this, simply divide the percentage by 100. For 50%, this would be 50/100 = 0.5. Then, multiply this decimal by the number you're finding the percentage of:
0.5 * 26 = 13
Again, this confirms that 50% of 26 is 13.
Method 3: Proportion Method
This method uses proportions to solve for the unknown value. We can set up a proportion as follows:
50/100 = x/26
Where 'x' represents the value we are trying to find (50% of 26). To solve for x, we can cross-multiply:
50 * 26 = 100 * x
1300 = 100x
x = 1300/100
x = 13
This confirms, once more, that 50% of 26 is 13.
Method 4: Using a Calculator
Modern calculators make percentage calculations incredibly simple. Most calculators have a percentage button (%) that directly performs this operation. Simply enter 26, press the multiplication button, enter 50, press the percentage button, and the calculator will display the result: 13.
Beyond the Basics: Exploring Different Percentage Calculations
While calculating 50% of 26 is relatively straightforward, the principles extend to calculating other percentages. Let's consider different scenarios and methods to tackle them.
Calculating 25% of 26:
25% is equivalent to 1/4. Therefore:
(1/4) * 26 = 26/4 = 6.5
Calculating 75% of 26:
75% is equivalent to 3/4. Therefore:
(3/4) * 26 = (3 * 26) / 4 = 78/4 = 19.5
Calculating 10% of 26:
10% is equivalent to 1/10. Therefore:
(1/10) * 26 = 26/10 = 2.6
Calculating x% of y:
The general formula for calculating x% of y is:
(x/100) * y
This formula allows you to calculate any percentage of any number. For instance, to find 37% of 85, you would substitute x with 37 and y with 85:
(37/100) * 85 = 0.37 * 85 = 31.45
Real-World Applications of Percentage Calculations
Percentages are ubiquitous in everyday life, impacting various aspects of our financial and personal lives:
- Sales and Discounts: Stores frequently advertise discounts as percentages (e.g., 20% off). Understanding percentages allows you to quickly calculate the final price after a discount.
- Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Calculating the total cost including tax requires understanding percentage calculations.
- Interest Rates: Interest rates on loans, savings accounts, and investments are presented as percentages. Knowing how to calculate interest is essential for financial planning.
- Tips and Gratuities: Calculating tips in restaurants usually involves determining a percentage (e.g., 15% or 20%) of the total bill.
- Grade Calculations: Many educational systems use percentages to represent grades and scores.
- Statistical Analysis: Percentages are frequently used to represent proportions and probabilities in statistical data analysis.
- Financial Statements: Companies use percentages extensively in their financial statements (e.g., profit margins, growth rates).
Frequently Asked Questions (FAQs)
-
Q: What if I need to calculate a percentage that isn't a whole number, like 33.33%?
A: The same principles apply. Convert the percentage to its decimal equivalent (33.33% = 0.3333) and multiply it by the number you're working with.
-
Q: How can I calculate the percentage increase or decrease between two numbers?
A: To calculate percentage increase or decrease, follow these steps:
- Find the difference between the two numbers.
- Divide the difference by the original number.
- Multiply the result by 100 to express it as a percentage.
-
Q: Are there any online calculators or tools that can help me with percentage calculations?
A: While I cannot provide external links, a simple internet search for "percentage calculator" will yield numerous free online tools that can assist with various percentage calculations.
Conclusion: Mastering Percentages for Everyday Life
Calculating 50% of 26, as demonstrated, is a fundamental application of percentage calculations. However, understanding the underlying principles and various methods for calculating percentages opens a door to numerous practical applications across diverse fields. From managing personal finances to analyzing data and understanding complex financial reports, the ability to perform percentage calculations confidently is an invaluable skill. The methods outlined in this article, ranging from basic fractional representations to the versatile general formula, equip you with the knowledge to tackle a wide range of percentage-related problems, empowering you to confidently navigate the numerical world around us. The seemingly simple task of finding 50% of 26 serves as a gateway to a deeper understanding of a fundamental mathematical concept with widespread real-world implications.
Latest Posts
Latest Posts
-
Gcf Of 36 And 28
Sep 23, 2025
-
Whats 22 C In Fahrenheit
Sep 23, 2025
-
16 5 As A Decimal
Sep 23, 2025
-
Convert 88 To A Fraction
Sep 23, 2025
-
Gcf For 12 And 30
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 50 Of 26 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.