What Is 70 Of 9
horsecheck
Sep 23, 2025 · 5 min read
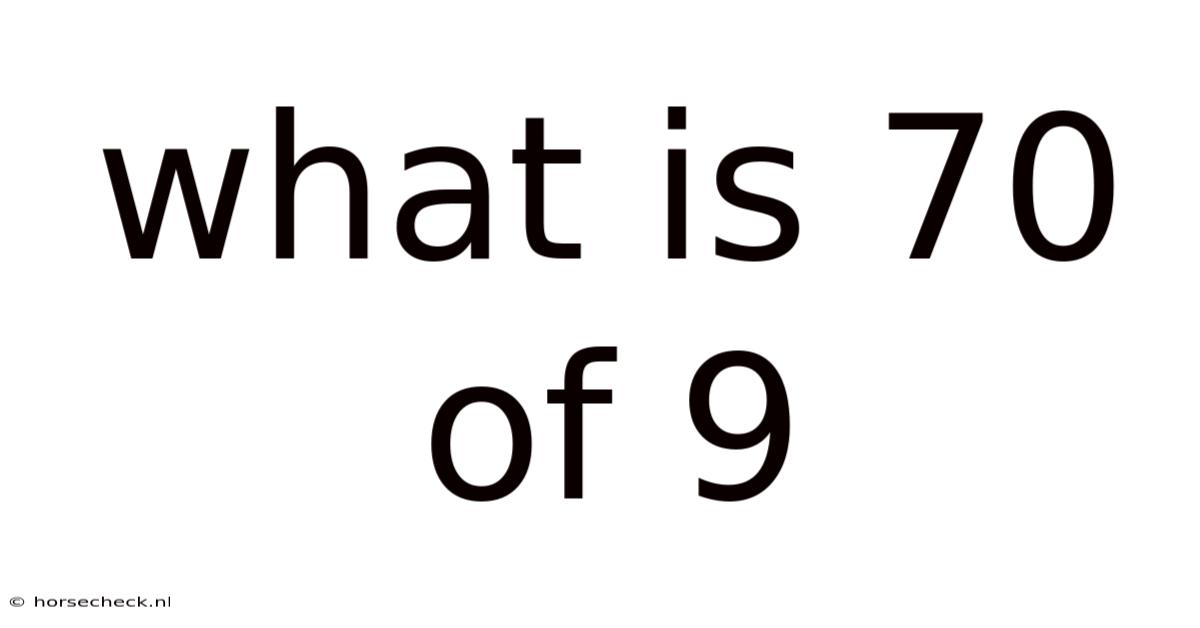
Table of Contents
What is 70% of 9? A Comprehensive Guide to Percentages and Their Applications
Finding 70% of 9 might seem like a simple arithmetic problem, but it's a gateway to understanding a fundamental concept in mathematics and its widespread applications in everyday life. This comprehensive guide will not only show you how to calculate 70% of 9 but will also delve into the broader understanding of percentages, their practical uses, and some common misconceptions. We'll explore different methods of calculation and even touch upon the historical context of percentages.
Understanding Percentages: A Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" literally means "out of one hundred" – per cent (Latin for "out of one hundred"). Therefore, 70% means 70 out of 100, or 70/100. This fraction can be simplified to 7/10. Understanding this fundamental relationship is key to solving percentage problems.
Method 1: Converting Percentage to Decimal
The most straightforward method to calculate 70% of 9 involves converting the percentage to its decimal equivalent. To do this, divide the percentage by 100:
70% ÷ 100 = 0.70 or 0.7
Now, multiply this decimal by the number you want to find the percentage of (in this case, 9):
0.7 * 9 = 6.3
Therefore, 70% of 9 is 6.3.
Method 2: Using Fractions
As mentioned earlier, 70% can be expressed as the fraction 70/100, which simplifies to 7/10. To find 70% of 9, we can multiply 9 by this fraction:
(7/10) * 9 = 63/10 = 6.3
This method reinforces the fractional representation of percentages and provides an alternative approach to the problem.
Method 3: Proportion Method
This method utilizes the concept of proportions to solve percentage problems. We can set up a proportion as follows:
70/100 = x/9
Here, 'x' represents the value we want to find (70% of 9). To solve for 'x', we cross-multiply:
70 * 9 = 100 * x
630 = 100x
x = 630/100 = 6.3
This method highlights the relationship between the percentage, the whole number, and the part we're trying to find.
Real-World Applications of Percentages
Percentages are ubiquitous in our daily lives. Understanding them is crucial for navigating various situations, including:
-
Finance: Calculating interest on loans or savings accounts, understanding discounts and sales tax, analyzing investment returns, budgeting personal finances. For example, if a bank offers a 3% interest rate on a savings account, knowing how to calculate percentages helps you understand how much interest your money will earn.
-
Shopping: Determining the discounted price of an item after a percentage discount, comparing prices and offers from different stores, calculating the total cost including sales tax. Knowing that a shirt is 20% off allows you to quickly calculate the final price.
-
Education: Grading systems often utilize percentages, reflecting the student's performance on exams and assignments. Understanding your percentage score helps you understand your standing in the class.
-
Science and Statistics: Percentages are fundamental in expressing data, particularly in statistical analysis. For example, representing survey results or scientific findings often involves the use of percentages.
-
Health and Nutrition: Nutritional labels use percentages to indicate the amount of various nutrients in food products. Understanding these percentages helps in making informed dietary choices.
Common Misconceptions About Percentages
-
Adding Percentages Directly: A common mistake is adding percentages directly without considering the base value. For instance, a 10% increase followed by a 10% decrease does not result in the original value. The final value will be slightly lower due to the compounding effect.
-
Confusing Percentage Change with Percentage Points: A change from 10% to 20% is a 10 percentage point increase, not a 100% increase. The percentage increase is calculated as [(20-10)/10] * 100% = 100%. This distinction is critical in interpreting data accurately.
-
Ignoring the Base Value: The base value is crucial in percentage calculations. For example, 10% of 100 is different from 10% of 1000. Failing to consider the base value can lead to incorrect calculations.
Beyond the Basics: Advanced Percentage Calculations
While finding 70% of 9 is a relatively simple calculation, more complex percentage problems can involve multiple steps, such as calculating percentage increase or decrease, finding the original value after a percentage change, or dealing with compound interest. These often require a deeper understanding of algebraic techniques and sometimes, the use of formulas.
Historical Context of Percentages
The concept of percentages has a rich history, with its roots in ancient civilizations. While the precise origin is difficult to pinpoint, the use of fractions and proportional relationships—the basis of percentages—can be traced back to ancient Babylonian and Egyptian mathematics. The modern notation using the "%" symbol emerged much later, likely in the 15th or 16th century. The symbol itself is thought to have evolved from the abbreviation "per cento," meaning "per hundred."
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a percentage increase or decrease?
- A: To calculate a percentage increase, find the difference between the new and original values, divide this difference by the original value, and then multiply by 100%. A percentage decrease is calculated similarly, but the result will be negative.
-
Q: How can I find the original value after a percentage change?
- A: This often requires working backwards using algebra. For example, if a value increased by 20% to become 120, you would solve the equation: x + 0.20x = 120, where 'x' is the original value.
-
Q: What are some common tools for calculating percentages?
- A: Calculators (both physical and digital), spreadsheets (like Microsoft Excel or Google Sheets), and online percentage calculators are all useful tools.
-
Q: Is there a formula for calculating percentages?
- A: While there isn't one single formula, the general approach is always to multiply the number by the decimal equivalent of the percentage. The formula can be written as:
Percentage = (Part / Whole) * 100orPart = (Percentage / 100) * Whole.
- A: While there isn't one single formula, the general approach is always to multiply the number by the decimal equivalent of the percentage. The formula can be written as:
Conclusion
Calculating 70% of 9, while seemingly trivial, provides a foundation for understanding percentages and their widespread application across various fields. Mastering percentage calculations enhances your ability to analyze data, make informed decisions, and solve numerous problems in daily life. From managing personal finances to understanding scientific data, a strong grasp of percentages is an invaluable skill. Remember the different methods presented in this guide—converting to decimals, using fractions, and the proportion method—and choose the approach that best suits your understanding and the problem at hand. By understanding the underlying principles and avoiding common misconceptions, you can confidently tackle a wide range of percentage problems and apply this knowledge to numerous real-world scenarios.
Latest Posts
Latest Posts
-
What Are The Multiples 3
Sep 23, 2025
-
Gcf Of 27 And 54
Sep 23, 2025
-
2 1 4 As Improper Fraction
Sep 23, 2025
-
Gcf Of 15 And 30
Sep 23, 2025
-
84 Out Of 100 Grade
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 70 Of 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.