What Is 80 Of 26
horsecheck
Sep 22, 2025 · 5 min read
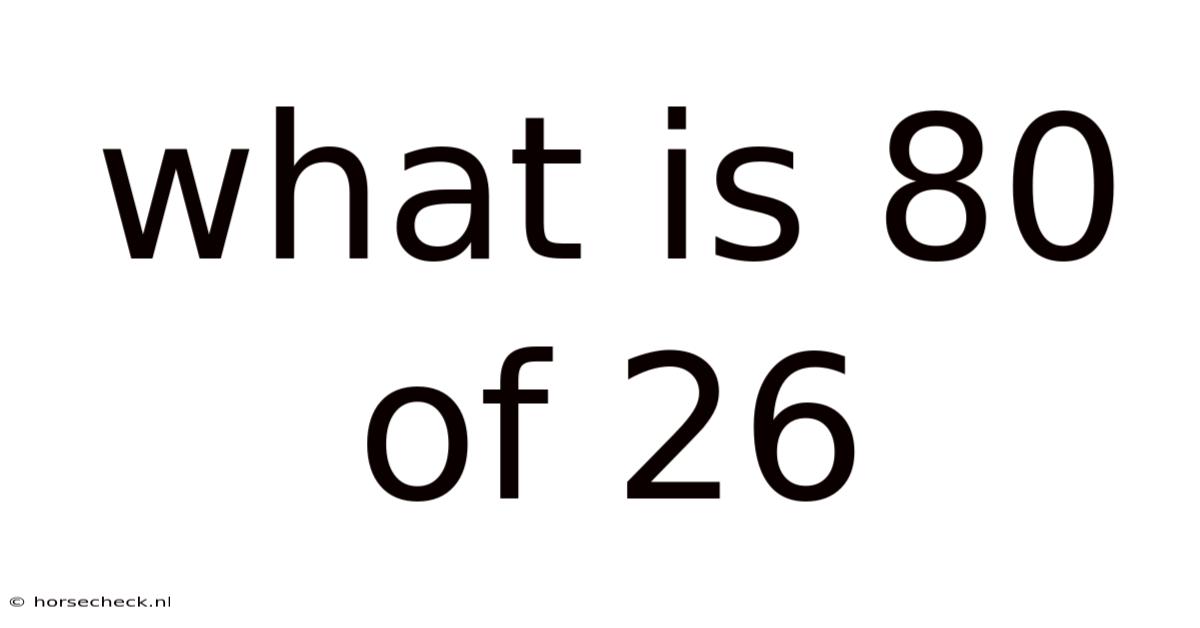
Table of Contents
What is 80% of 26? A Deep Dive into Percentages and Their Applications
Finding 80% of 26 might seem like a simple calculation, a quick task for a calculator. However, understanding the underlying principles of percentages and their practical applications extends far beyond this single problem. This article will not only solve this specific question but will also delve into the meaning of percentages, explore different methods for calculation, and showcase their relevance in various real-world scenarios. We'll also tackle common misconceptions and answer frequently asked questions.
Understanding Percentages: A Foundation
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" ("per cent" in Latin). So, 80% means 80 out of 100, which can be written as the fraction 80/100 or the decimal 0.8. This fundamental understanding is key to solving percentage problems.
Method 1: Converting to Decimal
The most straightforward method for calculating 80% of 26 is to convert the percentage to its decimal equivalent and then multiply.
-
Step 1: Convert the percentage to a decimal: Divide 80 by 100: 80 ÷ 100 = 0.8
-
Step 2: Multiply the decimal by the number: Multiply 0.8 by 26: 0.8 x 26 = 20.8
Therefore, 80% of 26 is 20.8.
Method 2: Using Fractions
Alternatively, we can use the fractional representation of 80%.
-
Step 1: Express the percentage as a fraction: 80% is equivalent to 80/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor (GCD), which is 20. This simplifies to 4/5.
-
Step 2: Multiply the fraction by the number: Multiply 4/5 by 26: (4/5) x 26 = 104/5
-
Step 3: Convert the improper fraction to a decimal: Divide 104 by 5: 104 ÷ 5 = 20.8
Again, we arrive at the answer: 80% of 26 is 20.8.
Method 3: Proportion Method
The proportion method offers a more visual and intuitive approach, particularly useful for understanding the underlying relationship between percentages and their corresponding values. We set up a proportion:
-
Step 1: Set up the proportion: We can represent the problem as a proportion: x / 26 = 80 / 100
-
Step 2: Cross-multiply: Cross-multiplying gives us: 100x = 80 x 26
-
Step 3: Solve for x: This simplifies to 100x = 2080. Dividing both sides by 100 gives us x = 20.8
Therefore, 80% of 26 is 20.8.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in many aspects of daily life and various professional fields. Here are some examples:
-
Sales and Discounts: Calculating discounts on items during sales events. For example, a 20% discount on a $50 item would be 0.20 x $50 = $10, resulting in a final price of $40.
-
Taxes: Determining the amount of sales tax or income tax owed.
-
Interest Rates: Calculating simple or compound interest earned on savings accounts or paid on loans. Understanding interest rates is vital for making informed financial decisions.
-
Financial Analysis: Analyzing financial statements like profit margins, return on investment (ROI), and market share often involves extensive use of percentage calculations.
-
Scientific Research: Percentages are frequently used to represent data and results in scientific research and statistical analysis. For example, expressing the success rate of a clinical trial or the percentage of a population with a specific trait.
-
Data Representation: Visualizing data through graphs and charts often requires converting raw data into percentages to make comparisons and trends easier to understand. For example, pie charts use percentages to represent different segments of a whole.
Common Misconceptions about Percentages
-
Adding percentages directly: A common mistake is to add percentages directly without considering the base value. For example, a 10% increase followed by a 10% decrease does not result in the original value. The base value changes after each percentage calculation.
-
Misunderstanding percentage change: Calculating percentage increase or decrease requires careful attention to the base value. A 20% increase on 100 is 120, but a 20% decrease from 120 is not 100; it's 96.
-
Confusing percentage points with percentages: A change of 10 percentage points is different from a 10% change. If something increases from 10% to 20%, that's a 10 percentage point increase, but a 100% increase (20/10 = 2). This distinction is critical in interpreting data and trends accurately.
Frequently Asked Questions (FAQs)
-
Q: How do I calculate a percentage of a number without a calculator?
- A: You can use the methods described above, utilizing fractions and manual multiplication and division. It may take longer but is perfectly achievable.
-
Q: What if I need to calculate a percentage that's not a whole number (e.g., 37.5%)?
- A: The same methods apply; simply convert the percentage (37.5%) to its decimal equivalent (0.375) and proceed with the multiplication.
-
Q: How can I check my percentage calculations?
- A: You can verify your calculations using different methods (decimal, fraction, proportion) to ensure accuracy. Using a calculator is also a reliable method for verification.
-
Q: Why is understanding percentages important?
- A: Percentages provide a standardized and readily understandable way to compare proportions and represent data, making it essential for various aspects of life, from personal finance to professional decision-making.
Conclusion
Calculating 80% of 26, which is 20.8, is only the starting point in understanding the broader world of percentages. This article has explored multiple methods for calculating percentages, highlighted their importance in diverse applications, and addressed common misconceptions. Mastering percentage calculations is a valuable skill that enhances numerical literacy and improves decision-making across numerous domains. The ability to confidently work with percentages empowers you to interpret data, make informed choices, and navigate the quantitative aspects of the world around you with greater ease and understanding. Remember to always focus on the base value and choose the method that best suits your understanding and the complexity of the problem at hand.
Latest Posts
Latest Posts
-
All The Factors For 18
Sep 22, 2025
-
64 To The 5 6 Power
Sep 22, 2025
-
The Cube Root Of 125
Sep 22, 2025
-
0 12 As A Fraction
Sep 22, 2025
-
134 Degrees F To K
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of 26 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.