Whats 75 Percent Of 50
horsecheck
Sep 25, 2025 · 5 min read
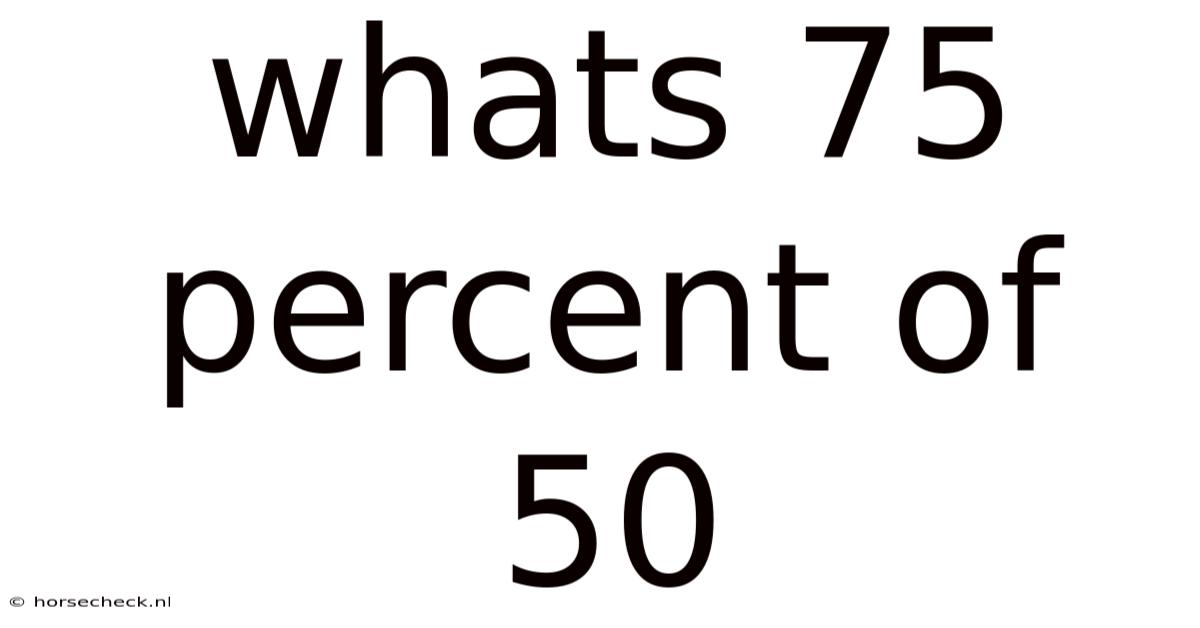
Table of Contents
What's 75 Percent of 50? A Deep Dive into Percentages and Their Applications
Finding 75% of 50 might seem like a simple arithmetic problem, suitable only for elementary school. However, understanding how to calculate percentages, and more importantly, the underlying concepts, is crucial for a wide range of applications in everyday life, from calculating discounts and taxes to understanding statistics and financial reports. This article will not only answer the question "What's 75 percent of 50?" but also explore the broader topic of percentages, offering different methods of calculation and highlighting their real-world relevance.
Understanding Percentages: The Fundamentals
A percentage is simply a fraction expressed as a part of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). Therefore, 75% means 75 out of 100, or 75/100. This fraction can be simplified to 3/4. Understanding this basic concept is the key to solving percentage problems.
Method 1: Using the Fraction Method
The most straightforward method to find 75% of 50 is to convert the percentage to a fraction and then multiply.
-
Step 1: Convert the percentage to a fraction: 75% = 75/100 = 3/4 (simplified)
-
Step 2: Multiply the fraction by the number: (3/4) * 50 = 150/4
-
Step 3: Simplify the fraction: 150/4 = 37.5
Therefore, 75% of 50 is 37.5.
Method 2: Using the Decimal Method
Another common method involves converting the percentage to a decimal and then multiplying.
-
Step 1: Convert the percentage to a decimal: 75% = 75/100 = 0.75
-
Step 2: Multiply the decimal by the number: 0.75 * 50 = 37.5
Again, we arrive at the answer: 75% of 50 is 37.5.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationship between percentages and proportions. We can set up a proportion:
-
Let x represent the unknown value (75% of 50).
-
We can write the proportion as: x/50 = 75/100
-
Cross-multiply: 100x = 75 * 50
-
Solve for x: 100x = 3750 => x = 3750/100 = 37.5
This method reinforces the idea that percentages represent a proportion of a whole.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is incredibly useful in many everyday situations:
-
Shopping and Sales: Calculating discounts. If a $100 item is on sale for 25% off, you can easily calculate the discount ($25) and the final price ($75).
-
Taxes: Determining the amount of sales tax or income tax to be paid.
-
Finance: Calculating interest earned on savings accounts or interest paid on loans. Understanding percentage changes in investments is crucial for financial planning.
-
Statistics: Interpreting data presented as percentages, such as survey results, election polls, or economic indicators. Understanding percentages helps you make sense of these data and draw informed conclusions.
-
Science and Engineering: Percentages are used extensively in scientific calculations and engineering designs, expressing concentrations, efficiencies, and error margins.
-
Everyday Life: Many situations involve estimations using percentages. For example, tipping in a restaurant (15-20% of the bill), calculating the percentage of a task completed, or determining the proportion of ingredients in a recipe.
Expanding the Understanding: Percentages Greater Than 100%
While the example above deals with a percentage less than 100%, it's important to note that percentages can also be greater than 100%. This simply means that the value in question exceeds the reference value. For instance, if a company's sales this year are 120% of last year's sales, it means the sales increased by 20%.
Calculating Percentage Increase and Decrease
Understanding percentage change is another important application. Let's say a quantity increases from 50 to 60. To calculate the percentage increase:
-
Find the difference: 60 - 50 = 10
-
Divide the difference by the original value: 10 / 50 = 0.2
-
Multiply by 100 to express as a percentage: 0.2 * 100 = 20%
Therefore, there is a 20% increase from 50 to 60.
Similarly, if a quantity decreases from 50 to 40, the percentage decrease is calculated as:
-
Find the difference: 50 - 40 = 10
-
Divide the difference by the original value: 10 / 50 = 0.2
-
Multiply by 100 to express as a percentage: 0.2 * 100 = 20%
Therefore, there is a 20% decrease from 50 to 40.
Frequently Asked Questions (FAQ)
-
Q: What if I need to find a different percentage of 50?
A: You can use any of the methods described above, simply substituting the desired percentage for 75%. For example, to find 20% of 50, you would calculate (20/100) * 50 = 10, or 0.20 * 50 = 10.
-
Q: Can I use a calculator to find percentages?
A: Yes, most calculators have a percentage function (%) that simplifies the calculation. Simply enter the number, press the percentage button, and then multiply by the other number.
-
Q: What if the percentage is not a whole number?
A: The same methods apply. For instance, to find 37.5% of 50, you would calculate (37.5/100) * 50 = 18.75, or 0.375 * 50 = 18.75.
-
Q: How do I calculate percentages mentally?
A: For some percentages, mental calculations are possible. For example, 10% of a number is simply the number divided by 10. 50% is half the number, 25% is a quarter of the number, and so on. Practicing these shortcuts can improve your mental arithmetic skills.
-
Q: Why is understanding percentages important?
A: Understanding percentages is crucial for navigating many aspects of life, from personal finance to professional contexts. It allows you to interpret data critically, make informed decisions, and solve problems efficiently.
Conclusion
Finding 75% of 50, while seemingly simple, opens the door to understanding the broader concept of percentages and their extensive applications. Mastering percentage calculations is a valuable skill that will serve you well in various aspects of your life. By understanding the underlying principles and employing the different calculation methods, you can confidently tackle percentage problems and interpret data effectively. Remember, practice is key to mastering this fundamental mathematical concept. The more you practice, the more comfortable and proficient you will become in applying percentages in your daily life.
Latest Posts
Latest Posts
-
Lcm Of 9 And 36
Sep 25, 2025
-
Algebra Equations That Equal 13
Sep 25, 2025
-
All The Factors Of 88
Sep 25, 2025
-
2 6 As An Improper Fraction
Sep 25, 2025
-
All The Factors Of 49
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about Whats 75 Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.