X 2 5 6 15
horsecheck
Sep 23, 2025 · 6 min read
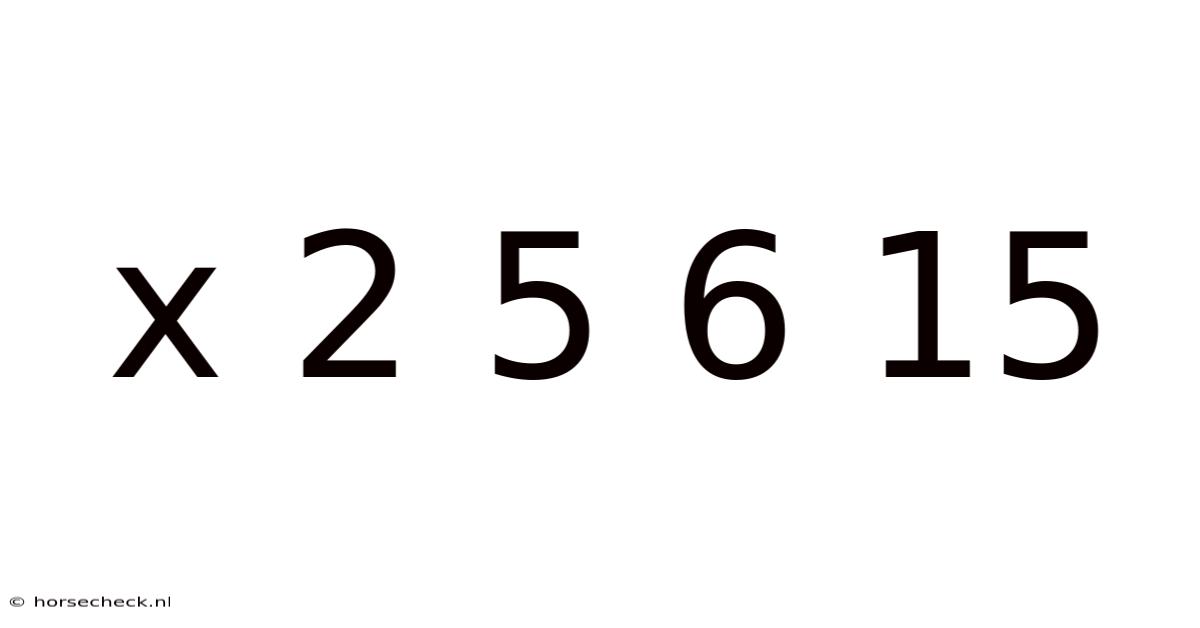
Table of Contents
Unlocking the Secrets of the Sequence: x 2 5 6 15 – A Mathematical Exploration
This article delves into the intriguing mathematical sequence: x 2 5 6 15. We'll explore various approaches to understanding the pattern, including potential mathematical operations, possible underlying rules, and the broader implications of sequence analysis. This exploration aims to not only find a solution for 'x' but also to develop a deeper understanding of mathematical reasoning and problem-solving techniques.
Introduction: The Allure of Number Sequences
Number sequences, seemingly simple strings of numbers, often hold hidden depths. They can represent patterns governed by specific mathematical rules, or they may be the output of complex algorithms. Analyzing these sequences sharpens critical thinking skills and enhances our ability to identify underlying structures in seemingly random data. The sequence x 2 5 6 15, with its unknown variable 'x', presents a particularly engaging challenge. Determining the value of 'x' necessitates a systematic exploration of potential mathematical operations and logical deductions. This isn't merely about finding a single answer; it's about embracing the process of mathematical investigation.
Potential Solutions and Mathematical Operations
Several approaches can be used to tackle this sequence. Let's examine a few possibilities:
1. Arithmetic Progressions: The most straightforward approach involves checking for arithmetic progressions – sequences where the difference between consecutive terms is constant. However, a quick glance reveals this isn't the case here. The differences between consecutive known terms (2-5 = -3, 5-6 = -1, 6-15 = -9) are inconsistent, ruling out a simple arithmetic progression.
2. Geometric Progressions: Next, let's consider geometric progressions, where the ratio between consecutive terms is constant. Again, this doesn't seem to hold true. The ratios (2/5 = 0.4, 5/6 ≈ 0.83, 6/15 = 0.4) are also inconsistent.
3. Exploring Combinations of Operations: Given the lack of simple arithmetic or geometric patterns, more complex combinations of operations might be at play. This could involve a mixture of addition, subtraction, multiplication, or division, possibly even involving powers or roots. Let's brainstorm some possibilities:
- Addition and Multiplication: Could there be a pattern involving adding and multiplying specific numbers? Let's try some trial and error. If we consider adding a constant and then multiplying, or vice-versa, we may find a consistent rule.
- Modulo Operations: Modulo operations (finding the remainder after division) could be involved. Exploring different modulo bases might reveal a hidden pattern.
- Hidden Fibonacci-like Patterns: While not a strict Fibonacci sequence (where each term is the sum of the two preceding terms), there might be a variation or a related pattern concealed within the sequence.
4. Polynomial Functions: It's possible that the sequence is generated by a polynomial function. For example, a quadratic function could fit the known points (assuming we assign indices to the terms: x is term 1, 2 is term 2, etc.). Finding a polynomial function that accurately predicts the subsequent terms would be strong evidence of the underlying rule. This would involve solving a system of equations, which can be done using various mathematical methods.
5. Recursive Relationships: The sequence might follow a recursive relationship, where each term is defined in terms of the preceding terms. This would require identifying the precise relationship between consecutive terms or groups of terms.
A Systematic Approach: Trial and Error and Deductive Reasoning
Let’s proceed methodically, combining trial and error with deductive reasoning. We will systematically explore different possibilities to identify a consistent pattern.
Let's start by trying simple additive and multiplicative combinations:
-
Scenario 1: x + a = 2, 2 + b = 5, 5 + c = 6, 6 + d = 15 This quickly becomes problematic as the differences (a, b, c, d) are inconsistent.
-
Scenario 2: x * a = 2, 2 * b = 5, 5 * c = 6, 6 * d = 15 Again, inconsistencies appear in the values of a, b, c, and d.
-
Scenario 3: Exploring Combinations: We can explore multiple combinations of addition, subtraction, multiplication, and division. For instance, could x be multiplied by a factor, then a number added or subtracted? Trial and error, using spreadsheet software or programming, would greatly facilitate this process.
The Importance of Context and Potential Ambiguity
The sequence x 2 5 6 15, without further context, might have multiple valid solutions. The "correct" answer depends on the underlying rule generating the sequence. This highlights the importance of context in mathematics. A single sequence can be generated by numerous rules. Without additional information or constraints, we may find several seemingly valid solutions.
Advanced Techniques: Polynomial Interpolation and Curve Fitting
For more complex sequences, more advanced mathematical techniques can be used. For instance, polynomial interpolation can be used to fit a polynomial function to the given data points. This involves solving a system of equations to determine the coefficients of the polynomial. Curve fitting is a broader concept that allows us to fit different types of functions (not just polynomials) to the data. Software like MATLAB, R, or even spreadsheet programs can perform these calculations efficiently.
Exploring Different Interpretations of the Sequence
Depending on the hidden rules governing the sequence, we might interpret the 'x' in different contexts. For example:
- x as the starting point of a recursive formula: We might find that x defines the initial term in a recursive relationship where subsequent terms are calculated based on preceding terms.
- x as a parameter in a function: 'x' could represent a parameter in a broader mathematical function that generates the sequence. This broader context might provide clues about its value.
- x as a component of a coded message: The sequence may not be purely mathematical but part of a coded message or puzzle, where 'x' plays a specific symbolic role.
The Role of Problem-Solving Strategies
Tackling this problem effectively demonstrates several important problem-solving strategies:
- Systematic Exploration: Instead of randomly guessing, we employ a structured approach, systematically exploring various possibilities.
- Trial and Error: We don’t shy away from experimenting with different approaches. Trial and error, especially when combined with logical reasoning, is a powerful tool.
- Deductive Reasoning: We use logical reasoning to eliminate possibilities that are inconsistent with the known terms.
- Pattern Recognition: We carefully examine the sequence to identify potential underlying patterns.
Conclusion: The Ongoing Search for Mathematical Patterns
Determining the value of 'x' in the sequence x 2 5 6 15 is a fascinating exercise in mathematical exploration. While there may not be a single definitive answer without further context, the process itself highlights several important concepts in mathematics and problem-solving. We have explored several potential approaches, from simple arithmetic operations to more advanced techniques such as polynomial interpolation. The journey itself, however, is just as valuable as finding a specific solution. It underscores the beauty and intricacy of mathematical patterns, encouraging a spirit of inquiry and a deeper appreciation for the power of logical reasoning. The seemingly simple sequence x 2 5 6 15 offers a gateway into a world of mathematical possibilities, inviting further exploration and investigation. The true challenge lies not just in finding an answer, but in developing the skills and the mindset to tackle such problems strategically and creatively. This quest for understanding patterns is the essence of mathematical exploration, and the sequence x 2 5 6 15 serves as a perfect microcosm of this larger intellectual pursuit.
Latest Posts
Latest Posts
-
Convert 200 Fahrenheit To Celsius
Sep 23, 2025
-
3 As A Whole Number
Sep 23, 2025
-
1 888 As A Mixed Number
Sep 23, 2025
-
Convert 104 F To Celsius
Sep 23, 2025
-
Convert 230 C To Fahrenheit
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about X 2 5 6 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.