0.54 Percent As A Decimal
horsecheck
Sep 21, 2025 · 5 min read
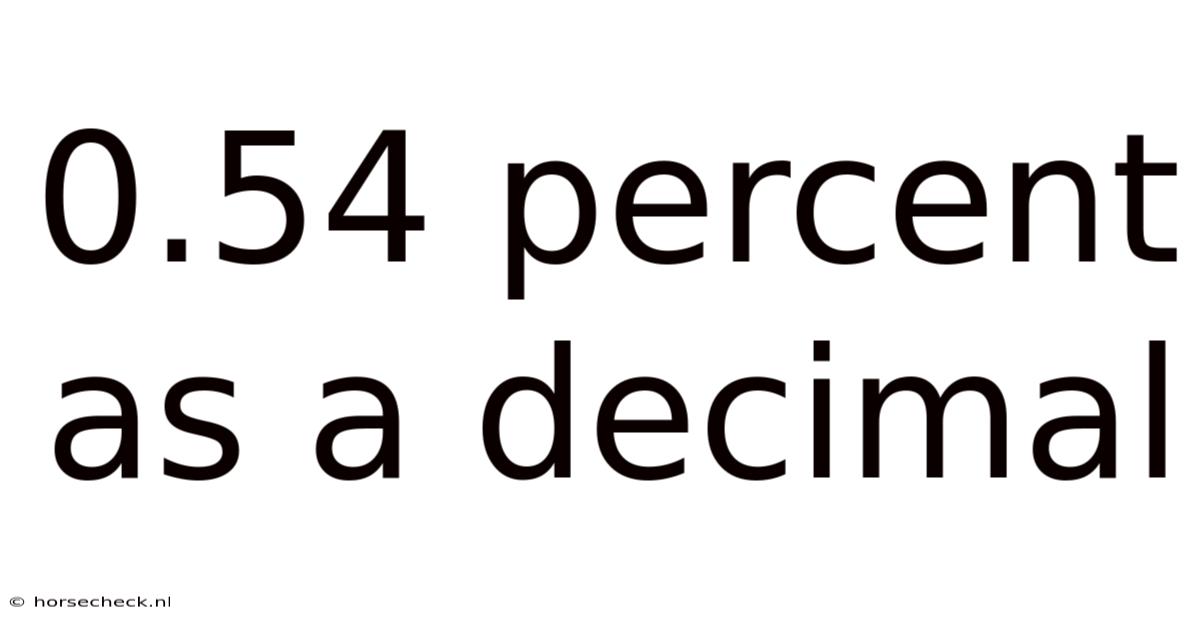
Table of Contents
Understanding 0.54 Percent as a Decimal: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics and has widespread applications in various fields, from finance and statistics to everyday life calculations. This comprehensive guide will delve into the conversion of 0.54 percent to its decimal form, explaining the process step-by-step and exploring related concepts to solidify your understanding. We'll cover the underlying principles, practical applications, and frequently asked questions to ensure you gain a thorough grasp of this important topic.
Introduction: Percentages and Decimals – A Necessary Relationship
Percentages and decimals are two different ways of representing the same numerical value. A percentage represents a fraction of 100, while a decimal represents a fraction in base 10. The ability to convert between these two forms is crucial for various calculations and interpretations. This article focuses specifically on understanding how to convert 0.54 percent into its decimal equivalent and what that means in practical terms. We'll explore the methodology behind the conversion and then discuss several real-world scenarios where this knowledge proves invaluable.
Converting 0.54 Percent to Decimal: A Step-by-Step Guide
The conversion of a percentage to a decimal involves a simple but important process. Remember that "percent" literally means "per hundred." Therefore, any percentage can be expressed as a fraction with a denominator of 100. Let's follow these steps to convert 0.54 percent to its decimal equivalent:
Step 1: Write the percentage as a fraction.
0.54% can be written as 0.54/100.
Step 2: Simplify the fraction (if possible).
While this fraction is already quite simple, we can express it as 54/10000 to remove the decimal point. This aids in understanding and clarifies the next step.
Step 3: Convert the fraction to a decimal.
To convert a fraction to a decimal, simply divide the numerator (top number) by the denominator (bottom number):
54 ÷ 10000 = 0.0054
Therefore, 0.54 percent as a decimal is 0.0054.
Understanding the Significance of the Decimal Value
The decimal 0.0054 represents a relatively small fraction. It signifies that for every 10,000 units, there are 54 units representing the 0.54%. This small value might seem insignificant on its own, but its importance becomes clear when dealing with large quantities or precise measurements. For example, in financial calculations, even small percentages can have a considerable impact over time due to compound interest.
Practical Applications: Where this Conversion is Useful
The conversion of percentages to decimals is vital in many real-world applications:
-
Finance: Calculating interest rates, discounts, tax rates, and profit margins often requires converting percentages to decimals. For example, if a bank offers a 0.54% interest rate, understanding its decimal equivalent (0.0054) is crucial for calculating the actual interest earned on a deposit.
-
Statistics: Representing data proportions and probabilities often involves decimals derived from percentages. For example, expressing a survey response rate as a decimal allows for easier statistical analysis and comparison with other datasets.
-
Science: Scientific measurements and calculations frequently involve precise decimal values, often derived from percentages. For example, in chemistry, the concentration of a solution might be expressed as a percentage, but calculations often require the decimal equivalent.
-
Everyday Life: Calculating sales discounts, tips, or understanding tax percentages relies on this conversion. For instance, when calculating a 0.54% discount on a purchase, converting the percentage to a decimal makes the calculation straightforward.
-
Computer Programming: Many programming languages use decimals to represent percentages for various calculations and data manipulations. Understanding how to convert between the two is fundamental for writing efficient and accurate code.
Further Exploration: Working with Larger and Smaller Percentages
While this article focuses on 0.54%, the same principles apply to any percentage. Let's briefly explore some examples to solidify your understanding:
-
Converting a larger percentage: Let's consider 12.5%. Following the steps outlined above:
- Write as a fraction: 12.5/100
- Simplify: This can be written as 125/1000 or 25/200, which simplifies further to 1/8
- Convert to decimal: 12.5 ÷ 100 = 0.125
-
Converting a smaller percentage: Let's take 0.02%.
- Write as a fraction: 0.02/100
- Simplify: This can be written as 2/10000
- Convert to decimal: 0.02 ÷ 100 = 0.0002
Mathematical Explanation: The Underlying Principles
The conversion process relies on the fundamental relationship between percentages and fractions. A percentage is simply a fraction with a denominator of 100. Therefore, converting a percentage to a decimal involves two steps:
-
Expressing the percentage as a fraction: This is done by writing the percentage number over 100.
-
Dividing the numerator by the denominator: This division converts the fraction into its equivalent decimal representation. Dividing by 100 is simply a matter of moving the decimal point two places to the left. This is why in the case of 0.54%, we obtain 0.0054.
Frequently Asked Questions (FAQ)
-
Q: Can I convert a decimal back to a percentage?
- A: Absolutely! To convert a decimal to a percentage, simply multiply the decimal by 100 and add the "%" symbol. For example, 0.0054 x 100 = 0.54%, confirming our initial conversion.
-
Q: What if the percentage has a fraction in it, like 2 1/2%?
- A: Convert the mixed number to an improper fraction first (5/2 in this example). Then, follow the same steps: (5/2)/100 = 5/200 = 2.5/100 = 0.025
-
Q: Are there any shortcuts for converting percentages to decimals?
- A: Yes! A quick shortcut is to move the decimal point two places to the left and remove the percentage sign. This works because dividing by 100 is the same as moving the decimal point two places to the left.
-
Q: Why is understanding this conversion important?
- A: It's essential for accurate calculations in many areas of life, enabling clear interpretation of data and efficient problem-solving across various disciplines.
Conclusion: Mastering Percentage-Decimal Conversions
Mastering the conversion between percentages and decimals is a critical skill with wide-ranging applications. Understanding the underlying principles, the step-by-step process, and the various practical applications of this conversion will enhance your mathematical proficiency and problem-solving abilities in various contexts. This knowledge will not only improve your understanding of mathematical concepts but also equip you with practical tools for tackling real-world problems effectively. Remember that the seemingly simple act of converting 0.54% to 0.0054 opens a door to a deeper understanding of numerical representation and its significance in diverse fields.
Latest Posts
Latest Posts
-
Gcf Of 40 And 15
Sep 21, 2025
-
1 4 X 2 3
Sep 21, 2025
-
Convert 42 C To Fahrenheit
Sep 21, 2025
-
What Is Equivalent To 5 10
Sep 21, 2025
-
Convert 63 Celsius To Fahrenheit
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 0.54 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.