1 4 X 2 3
horsecheck
Sep 21, 2025 · 4 min read
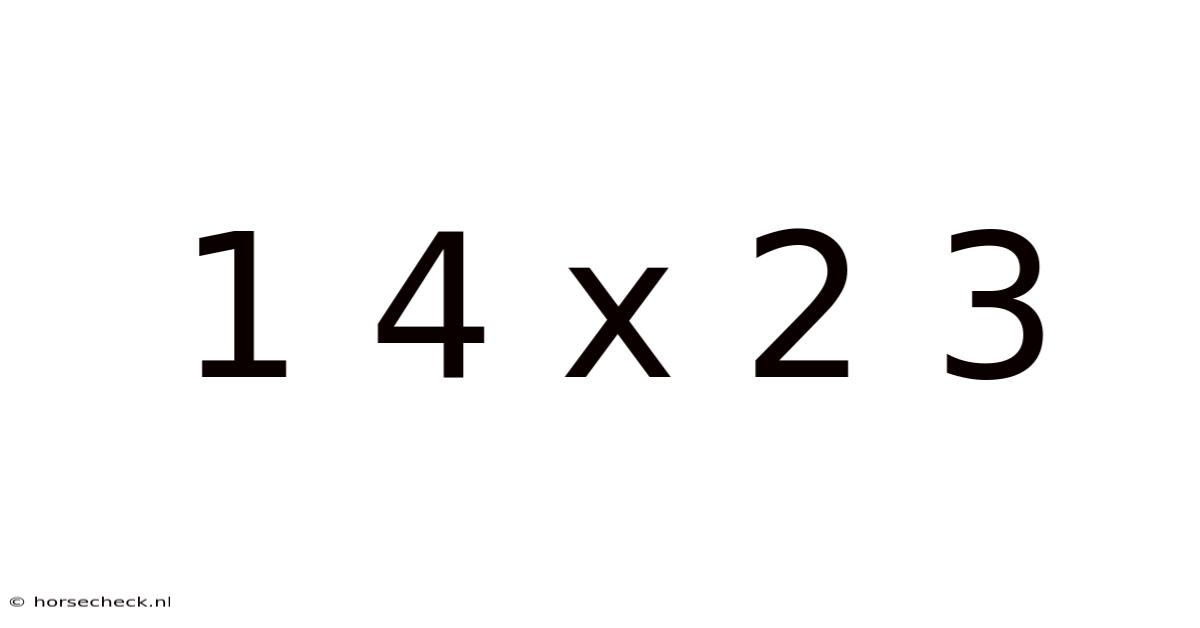
Table of Contents
Decoding the Mystery: A Deep Dive into 1 4 x 2 3
This article explores the seemingly simple mathematical expression "1 4 x 2 3," uncovering its complexities and demonstrating different interpretations depending on context. We'll delve into the order of operations, potential ambiguities, and the importance of clear notation in mathematics. Understanding this seemingly straightforward problem reveals fundamental principles crucial for mastering more advanced mathematical concepts. We'll cover everything from basic arithmetic to the nuances of mathematical notation, ensuring a comprehensive understanding for readers of all levels.
Introduction: The Importance of Order and Precision
The expression "1 4 x 2 3" might appear straightforward at first glance. However, its ambiguity highlights a critical aspect of mathematics: the importance of order of operations. Without a clearly defined order, multiple interpretations are possible, leading to different answers. This seemingly simple problem serves as a perfect illustration of why precise mathematical notation is paramount. This article aims to demystify this expression, exploring various interpretations and solidifying your understanding of fundamental mathematical principles.
Interpreting the Expression: Potential Meanings
The lack of explicit operators between the numbers introduces ambiguity. There are several ways to interpret this expression, each leading to a different result. Let's examine the possibilities:
1. Interpretation as Concatenation and Multiplication:
One possible interpretation treats the numbers as concatenated values followed by multiplication. This means:
- 14 x 23 = 322
This interpretation assumes the spaces are simply for readability and not representing separate operations.
2. Interpretation with Implicit Multiplication:
Another interpretation assumes implicit multiplication between the numbers. This could be represented as:
- (1)(4) x (2)(3) = 24
This interpretation considers each number pair as separate factors, multiplied together. It introduces parentheses to clarify the intended order of operations.
3. Interpretation as a Single Number with Implicit Decimal:
A third interpretation, although less likely given common mathematical notation, might consider it as:
- 1.4 x 2.3 ≈ 3.22
This assumes the spaces represent decimal points, resulting in a decimal multiplication. However, this is less probable due to the lack of standard decimal notation.
The Order of Operations: PEMDAS/BODMAS
To avoid ambiguity, mathematicians use the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same order of operations. Applying these rules clarifies how expressions should be evaluated. However, the lack of parentheses or explicit operators in "1 4 x 2 3" makes applying these rules directly challenging.
Resolving the Ambiguity: The Need for Explicit Notation
The ambiguity in "1 4 x 2 3" underscores the crucial role of clear and unambiguous mathematical notation. To avoid confusion, we should always use:
- Parentheses: Clearly indicate the order of operations. For example: (14 x 23), (1 x 4) x (2 x 3), or 1.4 x 2.3.
- Explicit Operators: Use the multiplication symbol "x" or "*" explicitly between numbers to avoid potential misinterpretations.
Mathematical Notation: Beyond the Basics
Mathematical notation is a precise language designed to avoid ambiguity. The importance of precise notation is not just for solving simple expressions like "1 4 x 2 3." As we move to more complex equations, clear notation becomes absolutely essential for preventing errors and ensuring accuracy. Concepts such as matrix multiplication, vector operations, and calculus heavily rely on consistent and well-defined notation.
Practical Applications: Real-World Examples of Order of Operations
The principles illustrated by the "1 4 x 2 3" problem are fundamental to many real-world applications. Consider these examples:
- Programming: Programming languages strictly adhere to order of operations. Understanding these rules is essential for writing error-free code.
- Engineering: Calculations in engineering, especially those involving multiple variables and units, require strict adherence to the order of operations for accurate results.
- Finance: Financial calculations, such as compound interest or loan amortization, rely heavily on correct order of operations.
Frequently Asked Questions (FAQ)
Q: What is the correct answer to "1 4 x 2 3"?
A: There is no single "correct" answer without clarifying the intended order of operations. The lack of explicit operators and parentheses makes multiple interpretations possible, each resulting in a different answer (322, 24, or approximately 3.22 depending on interpretation).
Q: Why is mathematical notation so important?
A: Precise mathematical notation prevents ambiguity and ensures that everyone interprets an expression in the same way. This is crucial for accurate calculations and communication in all fields involving mathematics.
Q: How can I avoid making similar mistakes?
A: Always use explicit operators (e.g., x or *) and parentheses to clearly indicate the order of operations. Never rely on implied operations or ambiguous spacing.
Conclusion: The Lesson Learned
The seemingly simple expression "1 4 x 2 3" serves as a powerful reminder of the importance of clear, unambiguous mathematical notation and the strict adherence to the order of operations. The multiple interpretations highlight the potential for miscommunication and errors when these principles are not followed. By understanding the order of operations and utilizing precise notation, we can confidently navigate more complex mathematical problems and avoid ambiguity. This fundamental understanding lays the groundwork for success in more advanced mathematical studies and real-world applications. Always remember to prioritize clarity and precision in your mathematical work. The simple problem of "1 4 x 2 3" has much to teach us about the rigor and precision demanded by the field of mathematics.
Latest Posts
Latest Posts
-
Square Root Of 74 Simplified
Sep 22, 2025
-
Two Thirds Divided By Three
Sep 22, 2025
-
25 64 Vs 3 8
Sep 22, 2025
-
Divide 30 By 1 2
Sep 22, 2025
-
177 Degrees Celsius To Fahrenheit
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1 4 X 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.