1 6 Multiplied By 2
horsecheck
Sep 23, 2025 · 6 min read
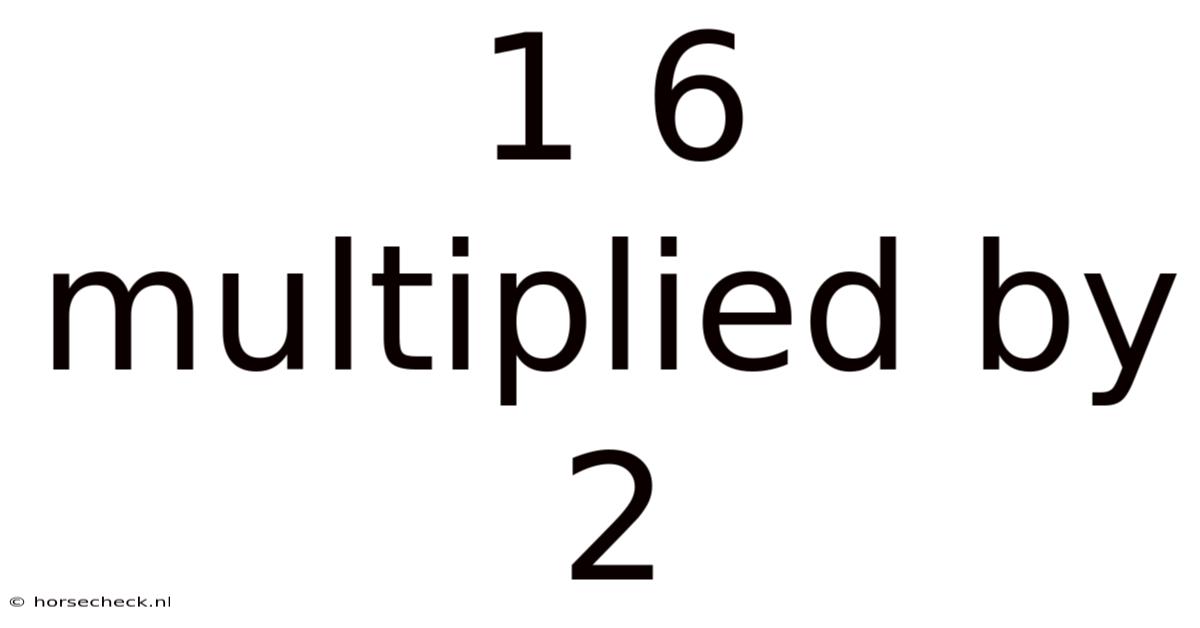
Table of Contents
Unpacking the Simple Equation: 16 Multiplied by 2
This seemingly straightforward equation, 16 multiplied by 2, offers a fantastic opportunity to explore fundamental mathematical concepts and delve deeper than a simple answer of 32. This article will unpack this equation, exploring its various interpretations, applications, and underlying principles, catering to readers of all levels, from elementary school students to those looking for a refresher in basic arithmetic. We will examine the equation through various lenses, moving from concrete examples to abstract mathematical principles, ensuring a comprehensive and engaging learning experience.
Understanding Multiplication: A Foundation
Before we dive into the specifics of 16 multiplied by 2, let's establish a solid understanding of what multiplication actually is. Multiplication is a fundamental arithmetic operation that essentially represents repeated addition. When we say 16 multiplied by 2 (often written as 16 x 2 or 16 * 2), we're essentially saying "add 16 to itself two times". This simple definition forms the bedrock of understanding more complex mathematical concepts.
Consider this scenario: Imagine you have two bags of apples, and each bag contains 16 apples. To find the total number of apples, you could add 16 + 16, or you could use multiplication: 16 x 2. Both methods will yield the same result: 32 apples. This exemplifies the practical application of multiplication in everyday life.
Visualizing 16 x 2: Concrete Representations
Visual aids can significantly enhance understanding, especially for younger learners. Let's visualize 16 x 2 using different methods:
-
Arrays: We can represent 16 x 2 as a rectangular array. Imagine a rectangle with 16 rows and 2 columns. Counting the total number of squares in the rectangle would give us the answer, 32. This visualization helps to solidify the connection between repeated addition and multiplication.
-
Groups: Imagine 2 groups of objects, with 16 objects in each group. Whether it's apples, marbles, or even abstract units, counting the total number of objects in both groups provides a tangible representation of the multiplication.
-
Number Line: A number line can also help visualize the process. Starting at 0, you would jump 16 units to reach 16, then jump another 16 units to reach 32. This visual representation emphasizes the repeated addition aspect of multiplication.
The Commutative Property: Changing the Order
A crucial property of multiplication is the commutative property. This property states that the order of the numbers in a multiplication equation doesn't affect the result. In other words, 16 x 2 is the same as 2 x 16. Both equations will always equal 32. This seemingly simple property has profound implications in more advanced mathematical operations.
Understanding this allows for flexibility in problem-solving. Sometimes, it’s easier to calculate 2 x 16 (doubling 16) than 16 x 2. This understanding allows us to choose the most efficient approach for calculation.
Different Methods of Calculation: Beyond Simple Addition
While repeated addition is the foundation, several methods can calculate 16 x 2 efficiently:
-
Mental Math: For many, 16 x 2 is easily calculated mentally. Doubling 16 is a relatively straightforward mental calculation.
-
Standard Algorithm: The standard multiplication algorithm involves multiplying each digit of 16 by 2, starting with the ones place, and then carrying over any tens to the tens place. This method is systematically taught in schools and provides a structured approach for more complex multiplications.
-
Distributive Property: The distributive property is a powerful tool in mathematics. It allows us to break down a multiplication problem into smaller, more manageable parts. For instance, we can rewrite 16 as 10 + 6. Then, applying the distributive property, we get: 2 x (10 + 6) = (2 x 10) + (2 x 6) = 20 + 12 = 32. This demonstrates the flexibility and power of breaking down complex operations into simpler ones.
Applying 16 x 2: Real-World Applications
The equation 16 x 2 finds its application in numerous real-world scenarios:
-
Shopping: Calculating the cost of two items that each cost $16.
-
Baking: Doubling a recipe that calls for 16 grams of flour.
-
Construction: Calculating the total length of two pieces of wood, each measuring 16 inches.
-
Travel: Calculating the distance traveled in two hours at a speed of 16 miles per hour.
These examples highlight the practical relevance of understanding even the simplest multiplication problems. The ability to perform quick and accurate calculations is a valuable skill in various aspects of daily life.
Extending the Concept: Beyond Basic Multiplication
Understanding 16 x 2 provides a springboard for exploring more advanced concepts:
-
Multiplication with Larger Numbers: This basic equation is a building block for multiplying larger numbers. The same principles apply, whether multiplying by tens, hundreds, or thousands.
-
Algebra: The concept extends seamlessly into algebra, where variables replace numbers. For instance, 2x = 32 would require solving for x, which involves applying the inverse operation of multiplication (division).
-
Geometry: Multiplication is crucial in calculating areas and volumes of geometric shapes. Understanding 16 x 2 is a stepping stone towards understanding more complex geometric calculations.
Frequently Asked Questions (FAQs)
Q: What is the easiest way to calculate 16 x 2?
A: The easiest way depends on individual preference and mathematical skills. Mental math (doubling 16) is often the quickest for many. The standard algorithm provides a structured approach suitable for all levels.
Q: Why is the order of numbers in multiplication unimportant?
A: This is because of the commutative property of multiplication. It's a fundamental property of the operation that allows for flexibility in calculation.
Q: How can I teach 16 x 2 to a young child?
A: Use visual aids like objects, arrays, or number lines. Relate the equation to real-world scenarios that the child can understand. Start with repeated addition to build a conceptual understanding before moving to the multiplication symbol.
Q: Are there any tricks for memorizing multiplication facts?
A: Yes, there are various memory techniques, including flashcards, songs, and visual aids. Repetition and consistent practice are key to memorization.
Conclusion: The Significance of a Simple Equation
While 16 multiplied by 2 might seem like a trivial equation, its significance extends far beyond a simple answer of 32. This equation serves as a foundational element in understanding fundamental mathematical principles, including repeated addition, the commutative property, and the distributive property. Its application spans various fields, from everyday calculations to more complex mathematical concepts. Mastering this simple equation lays the groundwork for tackling more challenging mathematical problems in the future, emphasizing the importance of building a strong foundation in basic arithmetic. The ability to understand and apply this seemingly simple equation opens doors to a deeper appreciation of mathematics and its pervasive influence on our world. So, the next time you encounter 16 x 2, remember the depth of knowledge and practical application it encapsulates.
Latest Posts
Latest Posts
-
Find 1 5 Of 25
Sep 23, 2025
-
21 And 24 Common Factor
Sep 23, 2025
-
What Equals 15 In Multiplication
Sep 23, 2025
-
Convert 39 C To F
Sep 23, 2025
-
5th Grade Math Review Worksheet
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 6 Multiplied By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.