Find 1 5 Of 25
horsecheck
Sep 23, 2025 · 5 min read
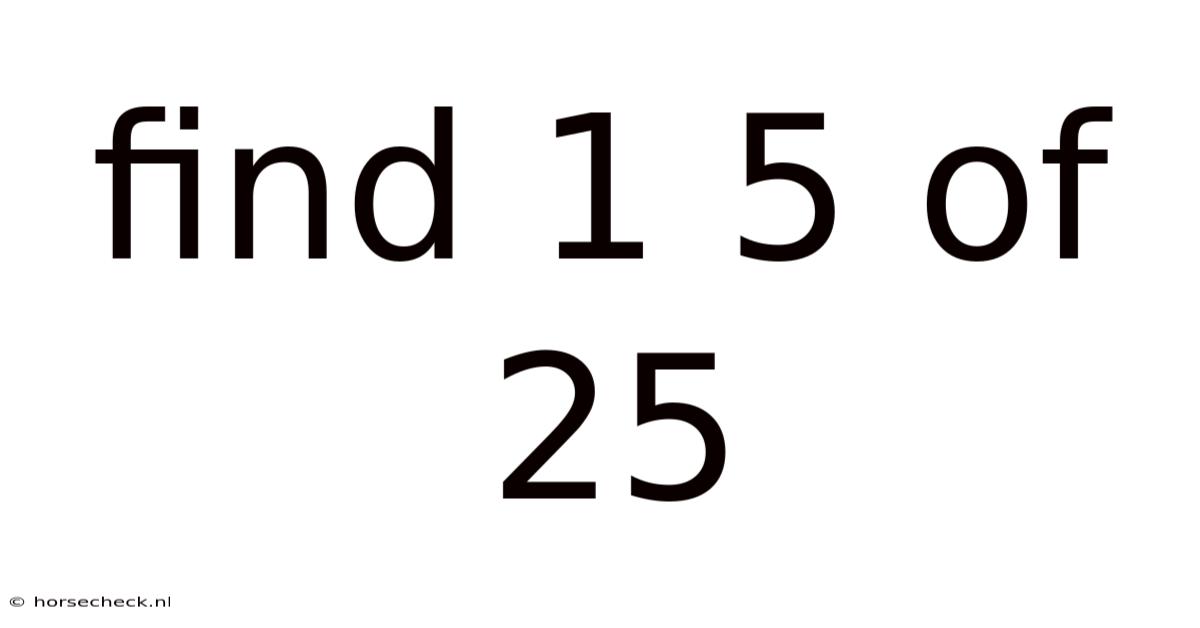
Table of Contents
Finding 1/5 of 25: A Comprehensive Guide to Fractions and Percentages
Finding a fraction of a number is a fundamental concept in mathematics, crucial for understanding percentages, ratios, and proportions. This guide will walk you through how to calculate 1/5 of 25, explaining the process in detail and exploring related concepts to build a strong foundation in fractional arithmetic. We'll cover different methods, provide practical examples, and answer frequently asked questions, ensuring you master this essential skill.
Understanding Fractions: The Building Blocks
Before we delve into finding 1/5 of 25, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. In the fraction 1/5, 1 is the numerator and 5 is the denominator. This means we're considering one part out of five equal parts.
Method 1: Division
The most straightforward method to find 1/5 of 25 is through division. The fraction 1/5 essentially means dividing the whole number (25 in this case) by the denominator (5).
Steps:
- Identify the whole number: Our whole number is 25.
- Identify the denominator: The denominator of our fraction (1/5) is 5.
- Divide the whole number by the denominator: 25 ÷ 5 = 5
Therefore, 1/5 of 25 is 5.
Method 2: Multiplication
Another approach is to use multiplication. Instead of directly dividing, we can multiply the whole number by the fraction.
Steps:
- Convert the fraction to a decimal: 1/5 can be expressed as a decimal by dividing the numerator (1) by the denominator (5): 1 ÷ 5 = 0.2
- Multiply the whole number by the decimal: 25 x 0.2 = 5
Again, we arrive at the answer: 1/5 of 25 is 5.
Method 3: Visual Representation
Visualizing the problem can be particularly helpful, especially for beginners. Imagine a pizza cut into 5 equal slices. Finding 1/5 of 25 is like finding the value of one slice if the whole pizza represents 25.
To solve visually:
- Divide the whole into equal parts: Divide 25 by 5 (the denominator) to find the value of each slice: 25 ÷ 5 = 5
- Determine the value of the required part: Since we're looking for 1/5, we take the value of one slice, which is 5.
This confirms that 1/5 of 25 is 5.
Expanding the Concept: Fractions and Percentages
Fractions and percentages are intrinsically linked. Percentages express a fraction out of 100. To convert a fraction to a percentage, we multiply the fraction by 100%.
Let's convert 1/5 to a percentage:
(1/5) x 100% = 20%
This means 1/5 is equivalent to 20%. So, finding 20% of 25 will also yield the same result:
(20/100) x 25 = 5
This reinforces the connection between fractions and percentages and provides another approach to solving similar problems.
Real-World Applications: Putting it into Practice
Understanding how to find a fraction of a number is not just an academic exercise; it has countless practical applications in everyday life. Consider these scenarios:
- Shopping Discounts: If a store offers a 20% discount on an item priced at $25, you can quickly calculate the discount using the knowledge gained above. A 20% discount (equivalent to 1/5) is $5 (20% of $25 = $5).
- Sharing Resources: If you have 25 candies and want to divide them equally among 5 friends, each friend gets 1/5 of the total, which is 5 candies.
- Recipe Scaling: If a recipe calls for 1/5 cup of sugar and you want to triple the recipe, you'll need 3 x (1/5 cup) = 3/5 cup of sugar. Understanding fractions helps you adjust recipes accurately.
- Financial Calculations: Calculating interest, discounts, or splitting bills often involves working with fractions and percentages.
Dealing with Larger Numbers and More Complex Fractions
The principles we’ve explored for finding 1/5 of 25 can be extended to more complex scenarios involving larger numbers and different fractions. The core concepts remain the same: division or multiplication, depending on the approach you prefer. For example, let's find 3/7 of 49:
Method 1 (Division):
- Divide 49 by the denominator (7): 49 ÷ 7 = 7
- Multiply the result by the numerator (3): 7 x 3 = 21
Therefore, 3/7 of 49 is 21.
Method 2 (Multiplication):
- Convert the fraction to a decimal: 3/7 ≈ 0.4286
- Multiply the whole number by the decimal: 49 x 0.4286 ≈ 21
Again, we get the answer 21.
Frequently Asked Questions (FAQ)
Q1: What if the fraction's denominator doesn't divide evenly into the whole number?
A1: In cases where the division doesn't result in a whole number, you'll get a decimal or a fraction as a result. For example, finding 1/3 of 25 would result in approximately 8.33 (25 ÷ 3 ≈ 8.33).
Q2: Can I use a calculator for these calculations?
A2: Absolutely! Calculators are helpful, particularly for more complex fractions or larger numbers. However, understanding the underlying principles is essential for problem-solving and avoiding errors.
Q3: What are some common fractions I should be familiar with?
A3: Familiarizing yourself with common fractions like 1/2, 1/3, 1/4, 1/5, 2/3, 3/4, and their decimal equivalents will greatly improve your ability to quickly estimate and calculate.
Q4: How can I improve my understanding of fractions?
A4: Practice is key! Solve various problems, use visual aids like diagrams and charts, and explore different methods. Online resources, educational videos, and textbooks offer valuable practice opportunities.
Conclusion: Mastering Fractions for a Brighter Future
Finding 1/5 of 25, while seemingly simple, forms the foundation for understanding and applying fractions and percentages in a myriad of situations. By mastering this basic concept and exploring the various methods and related concepts discussed in this guide, you'll enhance your mathematical skills, boosting your confidence in tackling more complex problems across various fields. Remember, consistent practice and a willingness to explore different approaches are crucial for building a strong mathematical foundation. So, keep practicing, and you’ll soon find that working with fractions becomes second nature!
Latest Posts
Latest Posts
-
What Grade Is A 8 12
Sep 23, 2025
-
What Is 15 Of 11
Sep 23, 2025
-
Six Tenths As A Decimal
Sep 23, 2025
-
What Is 8 Of 700
Sep 23, 2025
-
Maths Worksheet For Class 5
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Find 1 5 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.