1 9 Is Equal To
horsecheck
Sep 25, 2025 · 6 min read
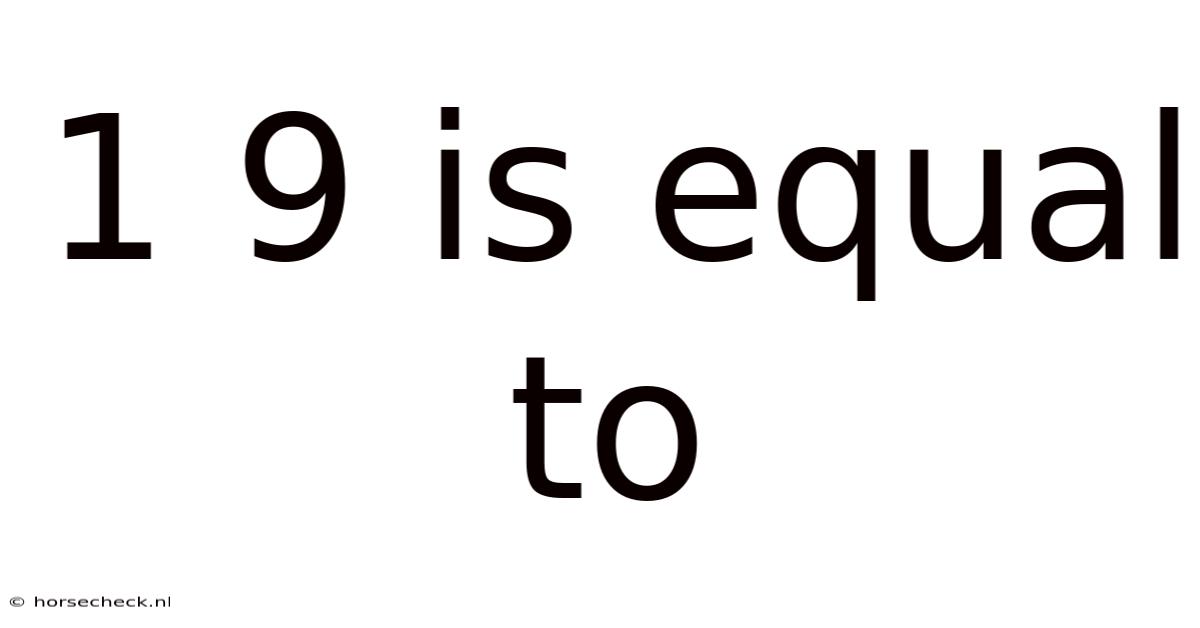
Table of Contents
19 is Equal To: Exploring the Mathematical and Philosophical Implications of a Simple Number
The seemingly simple statement, "19 is equal to 19," hides a wealth of mathematical concepts and even philosophical implications. While the equation itself is trivially true within the standard framework of arithmetic, delving deeper reveals the fascinating intricacies of number systems, mathematical operations, and the very nature of equality. This exploration goes beyond the simple assertion to uncover the profound meaning behind this seemingly mundane numerical expression.
Understanding the Basics: What Does "Equals" Mean?
Before we embark on our exploration, it's crucial to establish a clear understanding of the concept of equality in mathematics. The equals sign (=) signifies equivalence – a statement that two expressions represent the same value. In the case of "19 = 19," we're stating that the numerical representation "19" is equivalent to itself. This might seem self-evident, but it forms the foundational bedrock of numerous mathematical operations and theorems. Understanding this fundamental concept is key to grasping more complex mathematical ideas. It's not just about assigning a value; it's about establishing a relationship of equivalence.
Number Systems: Different Ways to Represent 19
While we readily recognize 19 in the base-10 decimal system, this number can be represented in countless ways using different number systems. This highlights the fact that "19" is not just a number; it's a representation of a quantity.
-
Binary (Base-2): In the binary system, used extensively in computer science, 19 is represented as 10011. This demonstrates that the same quantity can be expressed using different symbolic systems.
-
Hexadecimal (Base-16): In the hexadecimal system, frequently used in computing to represent colors and memory addresses, 19 is represented as 13. This illustrates the flexibility and efficiency of different number systems for representing numerical values.
-
Roman Numerals: In the Roman numeral system, 19 is represented as XIX. This shows how different cultures and historical periods have developed unique ways of representing numbers.
The variations in representation underscore the fact that "19 = 19" is true regardless of the chosen number system. The underlying quantity remains constant, even though its symbolic expression changes. This reinforces the concept of equality as a relationship independent of the specific representation.
Mathematical Operations and 19
The number 19 can be expressed as the result of various mathematical operations:
-
Addition: 10 + 9 = 19, 1 + 18 = 19, and countless other combinations.
-
Subtraction: 20 - 1 = 19, 100 - 81 = 19, showcasing the inverse relationship between addition and subtraction.
-
Multiplication: 1 x 19 = 19, highlighting the identity property of multiplication.
-
Division: 38 / 2 = 19, 57 / 3 = 19.
These examples demonstrate that 19 can be derived through numerous mathematical procedures, each validating its inherent value. The equation "19 = 19" holds true even when 19 is the result of a complex calculation. The equality remains consistent across different operational contexts.
Prime Factorization and the Uniqueness of 19
In number theory, prime factorization plays a crucial role. A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. 19 is a prime number; its only factors are 1 and itself. This unique prime factorization further solidifies the distinct identity of 19 within the number system. The fact that it's prime contributes to its fundamental character.
19 in Different Contexts: Beyond Pure Mathematics
The significance of 19 extends beyond pure mathematics. It appears in various contexts:
-
Physics: While not as prominent as some other numbers in physics, 19 might appear in specific calculations or measurements, albeit indirectly.
-
Chemistry: Again, its significance isn't directly apparent, but 19 could appear in calculations related to atomic weights or molecular formulas.
-
Culture and Society: The number 19 holds cultural significance in some societies, potentially influencing naming conventions, calendar systems, or artistic expressions. Researching specific cultural contexts can reveal deeper meanings.
This contextualization highlights that the seemingly simple "19 = 19" possesses relevance across disciplines. While it might not always be a central focus, understanding its mathematical foundations provides a broader understanding of its implications in different fields.
Philosophical Implications: Identity and Existence
From a philosophical perspective, the equation "19 = 19" can be interpreted in different ways:
-
Identity: It emphasizes the concept of self-identity. 19 is identical to itself; it possesses a unique and unchanging essence.
-
Existence: The equation implicitly affirms the existence of 19 as a valid and meaningful numerical entity within the established mathematical framework.
-
Truth: The statement is a tautology, a statement that is true by definition. This raises questions about the nature of truth and self-evident statements.
Exploring these philosophical implications showcases how a simple mathematical equation can spark deeper reflections on the nature of reality, identity, and the foundations of knowledge.
Addressing Potential Misunderstandings: Why Isn't it More Complicated?
The simplicity of "19 = 19" might lead some to question its significance. However, this simplicity is precisely its strength. It underlines the fundamental principles of mathematical equality, number systems, and the consistent nature of numerical identities. It serves as a building block for more complex mathematical concepts.
Frequently Asked Questions (FAQ)
Q: Can 19 be equal to anything other than 19?
A: No, within the standard framework of arithmetic, 19 can only be equal to 19. However, as explained earlier, it can be represented differently in various number systems.
Q: Is "19 = 19" a useful equation?
A: While it might seem trivial, it's crucial for establishing fundamental mathematical concepts and building upon them to solve more complex problems. It is the foundation upon which more complex equations are built.
Q: What is the significance of 19 being a prime number?
A: Being prime signifies its unique factorization, which is important in number theory and has implications for various mathematical proofs and algorithms.
Q: Are there any real-world applications of the concept "19 = 19"?
A: While the equation itself doesn't have direct, readily visible applications, the underlying concept of equality is fundamental to all quantitative measurements and calculations across various fields.
Conclusion: The Profound Simplicity of "19 = 19"
The seemingly simple statement, "19 is equal to 19," is far richer than it initially appears. This equation embodies fundamental mathematical principles, showcases the flexibility of different number systems, and even opens avenues for philosophical reflection on identity and existence. By exploring its various facets – from basic arithmetic to number theory and philosophical implications – we uncover a profound depth hidden within this simple numerical equivalence. The equation "19 = 19" serves as a potent reminder that even the simplest concepts can hold vast significance when examined closely. It is a cornerstone of mathematical understanding and a jumping-off point for deeper explorations into the fascinating world of numbers and their implications.
Latest Posts
Latest Posts
-
3 24 As A Percent
Sep 25, 2025
-
21 X What Equals 7
Sep 25, 2025
-
Gcf Of 35 And 15
Sep 25, 2025
-
What Is 30 Off 110
Sep 25, 2025
-
101 8 F To C
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 1 9 Is Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.