19 Is 25 Of What
horsecheck
Sep 23, 2025 · 5 min read
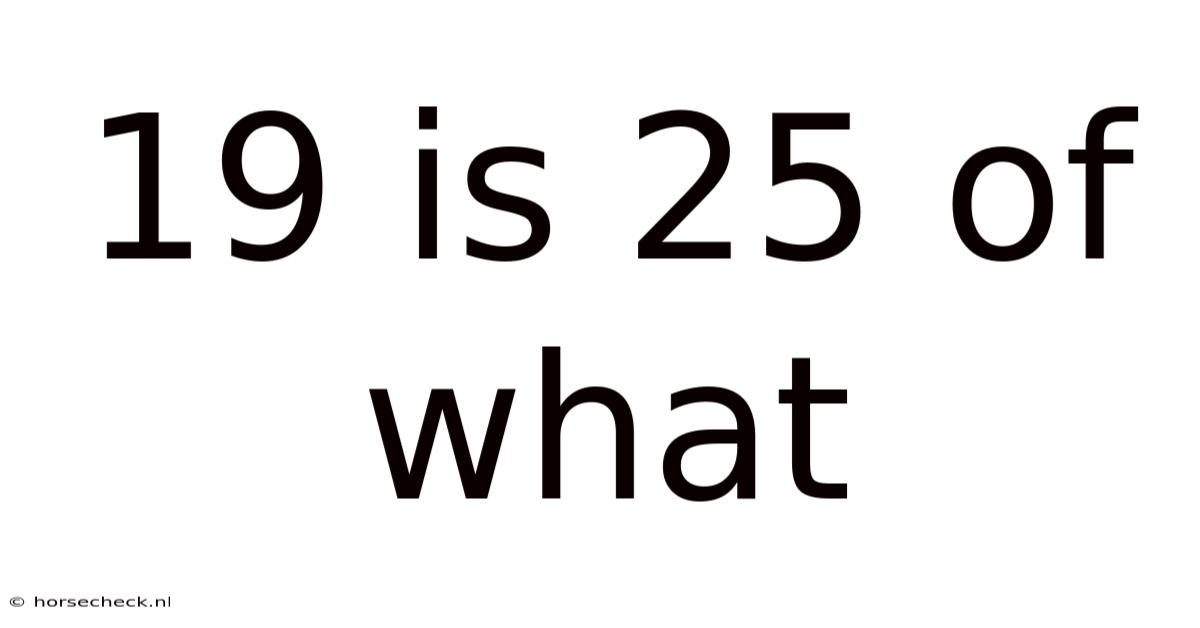
Table of Contents
19 is 25% of What: A Comprehensive Guide to Percentage Calculations
Finding out what number 19 represents 25% of requires understanding the fundamental concepts of percentages and how to solve percentage problems. This seemingly simple question opens the door to a deeper exploration of proportional reasoning, a crucial skill in mathematics and numerous real-world applications. This article will not only provide the solution but also delve into the underlying principles, offering multiple approaches to tackle such problems, and exploring practical examples to solidify your understanding.
Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100". For instance, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. Understanding this basic definition is crucial for solving percentage problems.
Method 1: Using the Formula
The most straightforward way to solve "19 is 25% of what" is by using the percentage formula:
Part = Percentage × Whole
In this case:
- Part is the value we know (19).
- Percentage is 25%, which we convert to a decimal by dividing by 100 (0.25).
- Whole is the unknown value we need to find (let's represent it with 'x').
Therefore, the equation becomes:
19 = 0.25 × x
To solve for x, we divide both sides of the equation by 0.25:
x = 19 / 0.25
x = 76
Therefore, 19 is 25% of 76.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent the problem as:
19/x = 25/100
This proportion reads: "19 is to x as 25 is to 100". To solve for x, we cross-multiply:
19 × 100 = 25 × x
1900 = 25x
Now, divide both sides by 25:
x = 1900 / 25
x = 76
Again, we find that 19 is 25% of 76.
Method 3: Working Backwards from the Percentage
Since 25% is a quarter (1/4), we can reason that if 19 is a quarter of a number, then the whole number must be four times larger. Therefore:
x = 19 × 4
x = 76
This method provides a quick and intuitive solution when dealing with easily recognizable percentages like 25%, 50%, and 75%.
Practical Applications: Real-World Examples
Understanding percentage calculations is essential in numerous real-life situations. Here are a few examples:
- Sales and Discounts: If an item is on sale for 25% off and costs $19 after the discount, what was the original price? Using the methods described above, the original price was $76.
- Taxes: Imagine you paid $19 in sales tax, and the tax rate is 25%. The pre-tax amount of your purchase was $76.
- Surveys and Statistics: If 25% of survey respondents (19 people) chose a particular option, the total number of respondents was 76.
- Financial Calculations: Percentage calculations are fundamental in understanding interest rates, investment returns, and loan repayments.
Expanding the Understanding: Beyond 25%
The methods explained above can be applied to any percentage calculation. For instance, let's say we want to find out what number 30 is 15% of. Using the formula:
30 = 0.15 × x
x = 30 / 0.15
x = 200
Therefore, 30 is 15% of 200.
Dealing with More Complex Percentages
While simple percentages like 25% and 15% are straightforward, you may encounter more complex percentages in real-world problems. For example:
- Finding a percentage of a percentage: This involves calculating percentages in multiple steps. For instance, if you have a 10% discount followed by a further 5% discount, you must calculate each discount step-by-step. It's crucial to remember that these discounts are not additive (15%).
- Calculating percentage increase or decrease: These situations involve determining the percentage change between two values. The formula for percentage change is: [(New Value - Old Value) / Old Value] × 100.
Frequently Asked Questions (FAQs)
Q1: What if the percentage is greater than 100%?
A1: A percentage greater than 100% indicates that the "part" is larger than the "whole." This often occurs when dealing with growth or increase. The same formula applies; you'll simply get a result where the "whole" is smaller than the "part".
Q2: How do I calculate percentages quickly in my head?
A2: For common percentages like 10%, 25%, and 50%, mental shortcuts are easy. 10% is one-tenth, 25% is one-quarter, and 50% is one-half. For other percentages, rounding to nearby easily calculable percentages can provide a close approximation.
Q3: Are there any online calculators or tools to help with percentage calculations?
A3: Many online calculators are available for performing percentage calculations quickly and accurately. These tools can be particularly helpful for complex calculations or when checking your work.
Conclusion: Mastering Percentage Calculations
Solving the problem "19 is 25% of what" is not just about finding the answer (76); it's about understanding the underlying principles of percentage calculations. By mastering various methods—from using formulas and proportions to employing mental math shortcuts—you equip yourself with a valuable skill applicable across various disciplines and real-life situations. This skill extends far beyond simple percentage problems; it's a building block for more advanced mathematical concepts and problem-solving strategies. Remember, practice is key to strengthening your understanding and improving your proficiency in percentage calculations. The more you practice, the more intuitive and efficient these calculations will become.
Latest Posts
Latest Posts
-
1 6 Is Equivalent To
Sep 23, 2025
-
What Is 28 Of 95
Sep 23, 2025
-
Convert 200 Fahrenheit To Celsius
Sep 23, 2025
-
3 As A Whole Number
Sep 23, 2025
-
1 888 As A Mixed Number
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 19 Is 25 Of What . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.