1 6 Is Equivalent To
horsecheck
Sep 23, 2025 · 6 min read
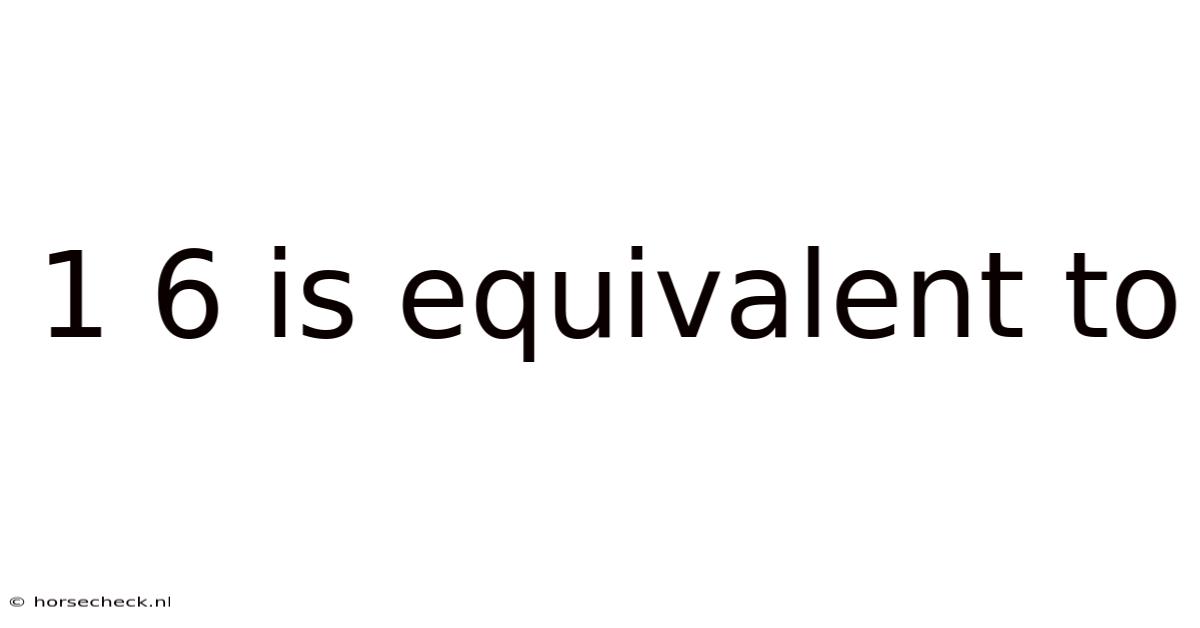
Table of Contents
1/6 is Equivalent To: Exploring Fractions and Their Representations
Understanding fractions is fundamental to mathematics and numerous real-world applications. This article delves deep into the concept of equivalence, specifically focusing on the fraction 1/6 and its various equivalent forms. We will explore different methods for finding equivalent fractions, their practical uses, and address frequently asked questions. By the end, you'll have a solid grasp of how to represent 1/6 in countless ways and understand the underlying mathematical principles involved.
Introduction: What Does "Equivalent" Mean in Fractions?
When we say two fractions are equivalent, it means they represent the same value or proportion. While they may look different—having different numerators and denominators—they occupy the same position on the number line. Think of it like different ways of expressing the same amount of pizza: 1/2 of a pizza is the same as 2/4 or 3/6. These are all equivalent fractions. This article will demonstrate how 1/6, a seemingly simple fraction, can be represented in numerous equivalent forms.
Methods for Finding Equivalent Fractions of 1/6
There are two primary methods for determining equivalent fractions:
-
Multiplying the Numerator and Denominator by the Same Number: This is the most straightforward approach. To find an equivalent fraction, multiply both the numerator (top number) and the denominator (bottom number) by the same non-zero integer. This is based on the fundamental principle that multiplying both the numerator and denominator by the same number doesn't change the overall value of the fraction. For example:
- 1/6 x 2/2 = 2/12
- 1/6 x 3/3 = 3/18
- 1/6 x 4/4 = 4/24
- 1/6 x 5/5 = 5/30
- 1/6 x 10/10 = 10/60
- and so on...
You can continue this process indefinitely, generating an infinite number of equivalent fractions for 1/6. Each fraction, despite its different appearance, represents the same portion of a whole.
-
Dividing the Numerator and Denominator by the Same Number (Simplifying Fractions): This method is the reverse of the first. It involves finding the greatest common divisor (GCD) of the numerator and denominator and then dividing both by that GCD to simplify the fraction to its lowest terms. Since 1/6 is already in its simplest form (1 and 6 share no common factors other than 1), we can't simplify it further using this method. However, this method is crucial when working with larger fractions that can be simplified. For instance, if we had 12/36, we would find the GCD (which is 12) and divide both the numerator and denominator by 12, resulting in 1/3 – a simplified equivalent fraction.
Visualizing Equivalent Fractions of 1/6
Visual aids can greatly enhance understanding. Imagine a rectangular pizza divided into six equal slices. One slice represents 1/6 of the pizza. Now, imagine dividing the same pizza into twelve equal slices. Two slices from this twelve-slice pizza represent the same amount of pizza as one slice from the six-slice pizza – this visually demonstrates that 1/6 is equivalent to 2/12. You can extend this visualization to other equivalent fractions by dividing the pizza into even more slices.
Applications of Equivalent Fractions: Real-World Examples
The concept of equivalent fractions is crucial in numerous practical situations:
-
Baking and Cooking: Recipes often require fractions of ingredients. Understanding equivalent fractions allows you to adjust recipes based on the available measurements. For example, if a recipe calls for 1/6 cup of sugar, but you only have a 1/12 cup measuring spoon, you know you need two 1/12 cup spoonfuls.
-
Measurement and Construction: In construction and engineering, accurate measurements are essential. Equivalent fractions aid in converting units and ensuring precise calculations.
-
Finance and Budgeting: When dealing with percentages and proportions of money, equivalent fractions become indispensable. Understanding how fractions relate helps in calculating interest, taxes, and other financial aspects.
-
Data Analysis and Statistics: Representing data in fractional forms is common. Equivalent fractions facilitate comparisons and interpretation of data across different scales.
-
Everyday Life: Dividing resources fairly, sharing items, and understanding proportions in various contexts all involve the use of fractions and their equivalencies.
Decimals and Percentages: Another Way to Represent 1/6
Besides fractions, we can express 1/6 using decimals and percentages:
-
Decimal: To convert 1/6 to a decimal, simply divide the numerator (1) by the denominator (6). This yields 0.16666... The sixes repeat infinitely, indicating a recurring decimal.
-
Percentage: To express 1/6 as a percentage, multiply the decimal equivalent by 100. 0.16666... x 100 ≈ 16.67%. Again, the percentage is approximate due to the recurring decimal.
Comparing and Ordering Fractions: The Role of Equivalent Fractions
When comparing fractions, particularly those with different denominators, finding equivalent fractions with a common denominator is invaluable. This allows for a direct comparison of the numerators. For instance, to compare 1/6 and 1/3, we can find an equivalent fraction for 1/3 with a denominator of 6: 1/3 = 2/6. Now we can easily see that 1/6 < 2/6, meaning 1/6 < 1/3.
Explaining Equivalent Fractions: A Deeper Dive into the Math
The principle behind equivalent fractions lies in the concept of proportionality. When we multiply both the numerator and denominator by the same number (say, 'k'), we're essentially multiplying the fraction by k/k, which is equal to 1. Multiplying any number by 1 doesn't change its value. Therefore, a/b = (ak)/(bk), where 'k' is any non-zero integer. This fundamental mathematical principle underpins the entire concept of equivalent fractions.
Frequently Asked Questions (FAQ)
-
Q: Is 1/6 the simplest form of the fraction?
- A: Yes, 1/6 is in its simplest form because the greatest common divisor of 1 and 6 is 1.
-
Q: Can a fraction have multiple equivalent fractions?
- A: Yes, infinitely many. You can keep multiplying the numerator and denominator by any non-zero integer to generate new equivalent fractions.
-
Q: How can I tell if two fractions are equivalent?
- A: If you can obtain one fraction by multiplying or dividing both the numerator and denominator of the other by the same non-zero number, then they are equivalent. Alternatively, you can convert both fractions to decimals and compare their values.
-
Q: Why is it important to understand equivalent fractions?
- A: Understanding equivalent fractions is crucial for simplifying calculations, comparing fractions, solving problems involving proportions, and applying fractional concepts to various real-world scenarios.
-
Q: What if I have a fraction that is not in its simplest form? How do I find its simplest equivalent?
- A: Find the greatest common divisor (GCD) of the numerator and denominator. Divide both the numerator and denominator by the GCD. The resulting fraction will be the simplest equivalent form.
Conclusion: Mastering the Equivalence of 1/6 and Beyond
Understanding the concept of equivalent fractions, specifically with 1/6 as an example, is a cornerstone of mathematical literacy. This article has explored multiple ways to represent 1/6, from multiplying and dividing the numerator and denominator to converting it to decimals and percentages. By mastering these techniques, you not only understand the equivalence of 1/6 but also gain a deeper comprehension of fractions and their applications in numerous areas of life. Remember, the ability to work comfortably with fractions unlocks a vast array of problem-solving skills across various disciplines. So keep practicing, and you’ll soon find that mastering fractions is easier than you think!
Latest Posts
Latest Posts
-
390 Degrees Fahrenheit To Celsius
Sep 23, 2025
-
2 875 As A Mixed Number
Sep 23, 2025
-
What Is 70 Of 9
Sep 23, 2025
-
What Grade Is A 14 15
Sep 23, 2025
-
What Is 50 Of 700
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 6 Is Equivalent To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.