2 41/50 As A Percent
horsecheck
Sep 23, 2025 · 5 min read
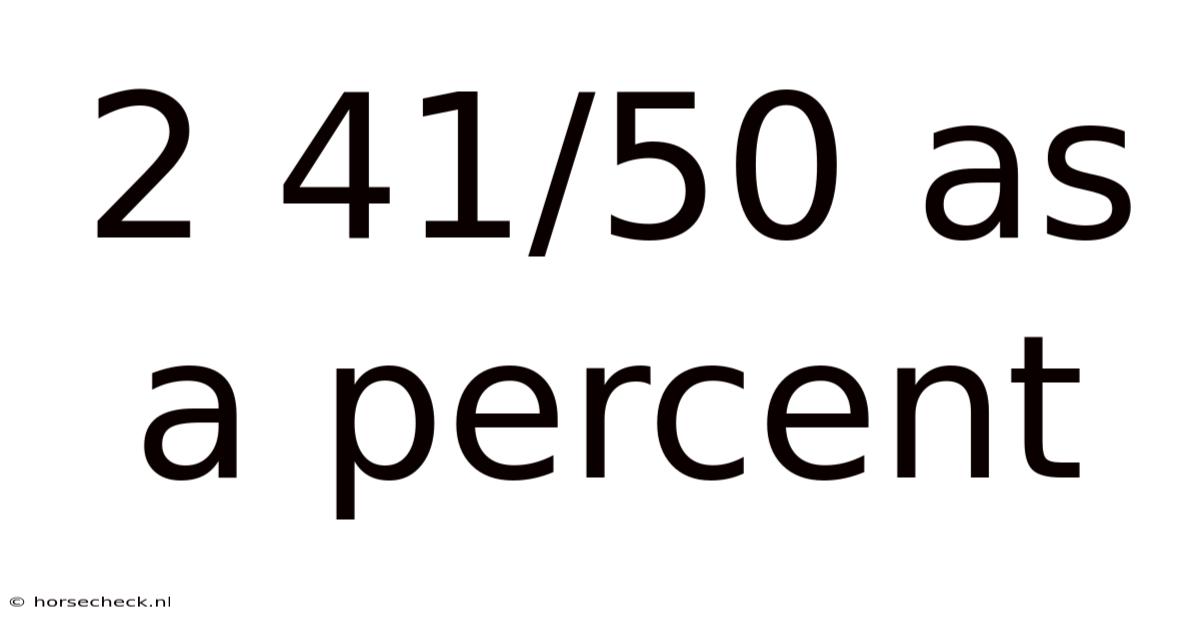
Table of Contents
Converting 2 41/50 to a Percent: A Comprehensive Guide
Understanding how to convert mixed numbers, like 2 41/50, into percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tax to understanding financial reports and statistics. This comprehensive guide will walk you through the process step-by-step, explaining the underlying concepts and providing examples to solidify your understanding. We'll cover various methods, address common misconceptions, and explore the practical uses of this conversion. By the end, you'll be confident in converting any mixed number to a percentage.
Understanding the Basics: Fractions, Decimals, and Percentages
Before diving into the conversion process, let's refresh our understanding of the three core concepts: fractions, decimals, and percentages.
-
Fractions: A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 41/50, 41 is the numerator and 50 is the denominator. This fraction represents 41 parts out of a total of 50 parts.
-
Decimals: A decimal is a way of expressing a fraction using a base-ten system. The decimal point separates the whole number part from the fractional part. For example, 0.82 is a decimal representing 82/100.
-
Percentages: A percentage is a way of expressing a fraction or decimal as a proportion of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 82% represents 82/100 or 0.82.
Method 1: Converting the Mixed Number to an Improper Fraction
The most straightforward method involves converting the mixed number 2 41/50 into an improper fraction, then converting the improper fraction to a decimal, and finally to a percentage.
Step 1: Convert the mixed number to an improper fraction.
To do this, we multiply the whole number (2) by the denominator (50) and add the numerator (41). This result becomes the new numerator, while the denominator remains the same.
2 41/50 = (2 * 50 + 41) / 50 = (100 + 41) / 50 = 141/50
Step 2: Convert the improper fraction to a decimal.
To convert a fraction to a decimal, we divide the numerator by the denominator:
141 ÷ 50 = 2.82
Step 3: Convert the decimal to a percentage.
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
2.82 * 100 = 282%
Therefore, 2 41/50 is equal to 282%.
Method 2: Converting the Mixed Number to a Decimal Directly
This method avoids the intermediate step of converting to an improper fraction.
Step 1: Convert the fractional part to a decimal.
Divide the numerator of the fraction (41) by the denominator (50):
41 ÷ 50 = 0.82
Step 2: Add the whole number.
Add the whole number part (2) to the decimal obtained in Step 1:
2 + 0.82 = 2.82
Step 3: Convert the decimal to a percentage.
Multiply the decimal by 100 and add the "%" symbol:
2.82 * 100 = 282%
Again, we arrive at the answer: 2 41/50 is equal to 282%.
Understanding the Result: What Does 282% Mean?
The result, 282%, signifies that the quantity represented by 2 41/50 is 282% of the original reference value. This implies that it is more than double the reference value (200%). In practical terms, if you consider "100%" as a whole, 282% is 2.82 times the original amount. This is a crucial point to remember when interpreting percentages exceeding 100%.
Practical Applications and Examples
Understanding percentage conversions is crucial in various real-world situations. Here are some examples:
-
Finance: Calculating interest rates, returns on investment (ROI), and understanding financial statements often involve percentage calculations. For instance, if your investment increased by 2 41/50 times its initial value, it grew by 282%.
-
Sales and Discounts: Calculating discounts, sales tax, and profit margins all rely on percentage calculations. A 282% markup on a product means its selling price is more than triple its cost price.
-
Statistics and Data Analysis: Percentages are used extensively in representing and analyzing data. For example, if a survey shows that 2 41/50 times more respondents prefer a particular product, the result is 282% higher preference for that product.
-
Science and Engineering: Percentages are used in expressing ratios, concentrations, and experimental results.
-
Everyday Life: Calculating tips, understanding unit pricing in supermarkets, and comparing deals all require familiarity with percentages.
Common Mistakes and How to Avoid Them
Several common mistakes can occur when converting mixed numbers to percentages. Let's address some of these:
-
Incorrectly converting mixed numbers to improper fractions: Ensure you correctly multiply the whole number by the denominator and add the numerator before dividing.
-
Forgetting to multiply by 100 when converting decimals to percentages: Remember that percentages are always out of 100; therefore, this multiplication step is essential.
-
Misinterpreting percentages over 100%: Percentages over 100% simply mean more than the whole. It is important to understand the context in which this occurs.
-
Rounding errors: When dealing with decimals, be mindful of rounding errors. Keep sufficient decimal places during calculations to minimize inaccuracies.
Frequently Asked Questions (FAQs)
Q: Can I convert the mixed number to a decimal first, then to a percentage? Yes, this is a perfectly valid method, as shown in Method 2.
Q: What if the fraction has a larger numerator than denominator? This results in an improper fraction which, when converted to a decimal, will be greater than 1. The corresponding percentage will be greater than 100%.
Q: How can I check my answer? You can reverse the process: convert the percentage back to a decimal, then a fraction to verify your initial calculation.
Q: Are there online calculators that can help with this? Yes, many online calculators are available to perform this conversion; however, understanding the underlying process is crucial.
Conclusion
Converting mixed numbers like 2 41/50 to percentages is a crucial skill with wide-ranging applications. By understanding the underlying principles of fractions, decimals, and percentages, and following the step-by-step methods outlined above, you can confidently perform this conversion. Remember to carefully consider the context of the percentage and its interpretation. Practice is key to mastering this skill; the more you work with these conversions, the more comfortable and confident you will become in your ability to handle them accurately and efficiently. Remember that 2 41/50 equates to 282%, highlighting that the value is significantly more than double the base value. This understanding is critical for interpreting results in various fields.
Latest Posts
Latest Posts
-
What Is 1 3 Of 24
Sep 23, 2025
-
What Grade Is A 9 16
Sep 23, 2025
-
3 4 6 In Fraction
Sep 23, 2025
-
Gcf Of 38 And 57
Sep 23, 2025
-
1 6 Multiplied By 2
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2 41/50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.