2 Times What Equals 72
horsecheck
Sep 25, 2025 · 6 min read
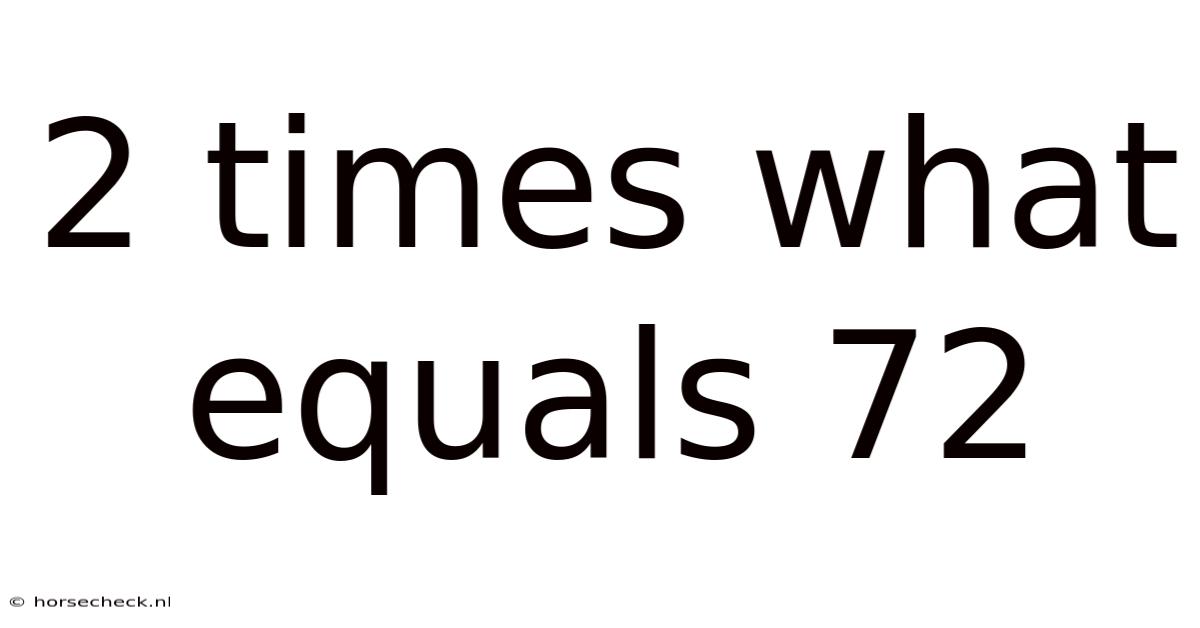
Table of Contents
Decoding the Mystery: 2 Times What Equals 72? A Deep Dive into Multiplication and Problem Solving
Finding the answer to "2 times what equals 72?" might seem simple at first glance. It's a basic multiplication problem, a cornerstone of elementary mathematics. However, this seemingly straightforward question opens a door to explore fundamental mathematical concepts, problem-solving strategies, and even the fascinating world of algebra. This article will delve into the solution, explain the underlying principles, and explore various ways to approach similar problems, ensuring a thorough understanding for learners of all levels.
Understanding the Problem: Unveiling the Basics
The core of the question, "2 times what equals 72," is a simple multiplication equation. We can represent this mathematically as:
2 * x = 72
Where 'x' represents the unknown number we're trying to find. This is a fundamental equation that forms the basis of many more complex mathematical concepts. Understanding this basic structure is crucial for progressing to more advanced mathematical topics.
Solving the Equation: The Direct Approach
The most straightforward method to solve this equation is to use division. Since multiplication and division are inverse operations, we can isolate 'x' by dividing both sides of the equation by 2:
2 * x / 2 = 72 / 2
This simplifies to:
x = 36
Therefore, 2 times 36 equals 72. This is the direct and most efficient way to solve this particular problem.
Exploring Alternative Approaches: Beyond Simple Division
While division provides the quickest solution, exploring alternative methods offers valuable insights into mathematical thinking and problem-solving skills. Let's consider a few:
-
Repeated Subtraction: Imagine you have 72 objects, and you want to divide them into two equal groups. You could repeatedly subtract 2 until you reach zero. The number of times you subtract 2 will give you the answer. While effective for smaller numbers, this method becomes cumbersome for larger equations.
-
Mental Math Techniques: With practice, you can develop mental math strategies to solve such problems quickly. For instance, recognizing that 72 is an even number and easily divisible by 2 might lead you directly to the answer through quick mental calculation. This method emphasizes the importance of number sense and familiarity with multiplication tables.
-
Using a Multiplication Table: A simple multiplication table can be a helpful tool, especially for learners who are still developing their multiplication skills. By looking at the "2" row in the table, you can locate the number 72 and find the corresponding column, revealing the answer – 36. This approach is particularly beneficial for visual learners.
-
Visual Representations: Visual aids can greatly aid understanding. Imagine representing 72 as a collection of objects. Then, you can divide them into two equal groups to visualize the solution. This is a particularly effective method for younger learners who benefit from concrete representations of abstract concepts.
Expanding the Concept: Introducing Algebra
The equation "2 * x = 72" is a basic algebraic equation. Algebra introduces the concept of using variables (like 'x') to represent unknown quantities. Solving algebraic equations involves manipulating the equation to isolate the variable and find its value. The techniques used to solve "2 * x = 72" are fundamental building blocks for solving more complex algebraic problems involving multiple variables and operations.
Real-World Applications: Where Does This Matter?
Understanding multiplication and solving equations like "2 times what equals 72" isn't confined to the classroom. It has numerous practical applications in everyday life:
-
Sharing and Dividing: Dividing resources equally among a group of people involves similar calculations. For example, if you have 72 candies to share equally among two friends, you would use the same principle to determine how many candies each person receives.
-
Cooking and Baking: Many recipes require precise measurements. If a recipe calls for double the amount of an ingredient, you'll need to use multiplication to determine the correct quantity.
-
Calculating Costs: If an item costs $2 each, and you want to spend a total of $72, you can use this equation to determine how many items you can buy.
-
Measurement and Conversions: Converting units of measurement often involves multiplication or division. For instance, converting meters to centimeters or pounds to ounces requires understanding how to scale the quantities.
Expanding on the Problem: Variations and Extensions
Let's consider variations and extensions of the original problem to further solidify our understanding:
-
What if the multiplier changes?: Instead of "2 times what equals 72," what if the question was "3 times what equals 72," or "5 times what equals 72?" The approach remains the same: divide 72 by the multiplier to find the unknown value. This emphasizes the versatility of the problem-solving method.
-
What if we introduce decimals?: What if the problem was "2.5 times what equals 72?" The approach remains fundamentally the same; simply divide 72 by 2.5. This introduces the concept of dividing by decimals, extending the problem's scope.
-
What if we use fractions?: "1/2 times what equals 72?" In this case, you would multiply 72 by the reciprocal of 1/2, which is 2, arriving at the same answer, emphasizing the interplay between fractions and division.
Addressing Common Mistakes and Misconceptions
While the problem seems straightforward, some common mistakes can occur, particularly among younger learners:
-
Confusing multiplication and addition: Some learners might attempt to add 2 repeatedly until they reach 72, which is incorrect. It’s crucial to emphasize the distinction between the two operations.
-
Incorrect division: Errors can arise during the division process, especially when dealing with larger numbers or decimals. Care and accuracy are vital throughout the calculation.
-
Forgetting the reciprocal in fraction problems: When dealing with fractions as multipliers, failing to use the reciprocal during the division step leads to an incorrect answer.
Frequently Asked Questions (FAQ)
-
Q: Can I solve this problem using a calculator? A: Absolutely! Calculators are valuable tools for efficient calculation, especially for larger numbers.
-
Q: Are there other ways to represent this problem? A: Yes, the problem can be represented in various ways, including word problems and visual diagrams, depending on the context and learning style.
-
Q: What are some real-world examples of using this type of calculation? A: Numerous examples exist, including splitting bills, calculating unit prices, converting measurements, and dividing resources.
Conclusion: Mastering the Fundamentals
The seemingly simple problem of "2 times what equals 72?" provides a gateway to exploring fundamental mathematical concepts, problem-solving strategies, and real-world applications. By understanding the different approaches to solving this equation, and by recognizing common mistakes, learners can build a solid foundation in mathematics. This problem serves as a springboard to tackle more complex mathematical challenges with confidence and competence. The ability to solve this type of problem is not just about finding the answer (36); it's about understanding the underlying principles and developing critical thinking skills that are essential for success in mathematics and beyond. Remember that practice is key – the more you work with these concepts, the more intuitive and effortless solving equations will become.
Latest Posts
Latest Posts
-
Convert 72 F To C
Sep 25, 2025
-
What Numbers Go Into 17
Sep 25, 2025
-
Factors Of 3 And 4
Sep 25, 2025
-
What Are Factors For 60
Sep 25, 2025
-
Whats The Decimal For 1 4
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 2 Times What Equals 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.