24 Times What Equals 4
horsecheck
Sep 24, 2025 · 5 min read
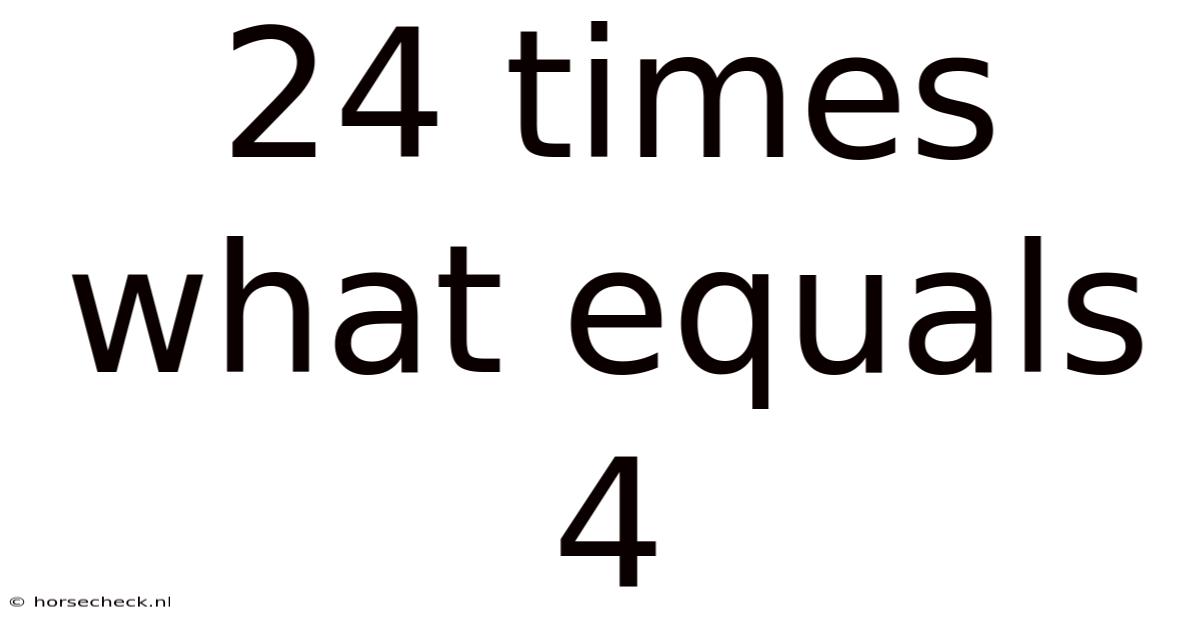
Table of Contents
Unveiling the Mystery: 24 Times What Equals 4? A Deep Dive into Division and its Applications
This article explores the seemingly simple equation, "24 times what equals 4," delving far beyond the immediate answer. We'll unravel the mathematical concepts involved, discuss various approaches to solving this type of problem, and explore practical applications in diverse fields. Understanding this seemingly basic equation opens doors to a deeper appreciation of mathematics and its relevance in everyday life.
Understanding the Problem: A Foundation in Division
The core of the question, "24 times what equals 4," lies in the fundamental mathematical operation of division. It's asking us to find a number that, when multiplied by 24, results in 4. This can be represented algebraically as:
24 * x = 4
Where 'x' represents the unknown number we're trying to find. To solve for 'x', we need to isolate it on one side of the equation. This involves performing the inverse operation of multiplication, which is division.
Method 1: Direct Division
The most straightforward approach is to divide both sides of the equation by 24:
x = 4 / 24
This simplifies to:
x = 1/6 or 0.1666...
Therefore, 24 times 1/6 (or approximately 0.1667) equals 4. This is the precise mathematical solution.
Method 2: Fractional Approach
Instead of immediately resorting to decimal division, we can work directly with fractions. We can express the equation as:
24 * x = 4
To solve for x, we divide both sides by 24:
x = 4/24
Now, simplify the fraction by finding the greatest common divisor (GCD) of 4 and 24, which is 4. Dividing both the numerator and denominator by 4 gives:
x = 1/6
This confirms our earlier result, highlighting the elegance and precision of working with fractions.
Method 3: Using Proportions
The problem can also be viewed as a proportion. We can set up a ratio:
24 / 4 = 1 / x
Cross-multiplying, we get:
24x = 4
Dividing both sides by 24:
x = 4/24 = 1/6
This method offers an alternative perspective, showcasing the versatility of proportional reasoning in solving mathematical problems.
Practical Applications: Beyond the Classroom
While this equation might seem elementary, the underlying principles of division and proportional reasoning have far-reaching applications in various fields:
-
Cooking and Baking: Scaling recipes up or down requires understanding proportions. If a recipe calls for 4 cups of flour and you only want to make a smaller portion, you'll need to calculate the appropriate amount of each ingredient based on the desired reduction.
-
Finance and Budgeting: Calculating percentages, interest rates, and proportions of income and expenses involves similar mathematical operations. Understanding how to manipulate these equations efficiently is crucial for financial literacy.
-
Engineering and Construction: Scaling blueprints, calculating material quantities, and determining ratios of mixtures all rely heavily on the ability to solve proportions and understand the relationship between different quantities.
-
Science and Data Analysis: Analyzing experimental data often involves calculating ratios, proportions, and averages. Scientists regularly use these mathematical tools to interpret results and draw conclusions.
-
Everyday Life: Dividing tasks, sharing resources fairly, or calculating the cost per unit of a product involves basic proportional reasoning. Even simple tasks require a sense of ratio and proportion.
Expanding the Concept: Exploring Related Problems
The core concept of solving "24 times what equals 4" extends to a broader range of problems involving multiplication and division. Let's examine some related scenarios:
-
Inverse Problems: What if the question were, "What number, when multiplied by 1/6, equals 4?" The solution is found by dividing 4 by 1/6, which is equivalent to multiplying 4 by 6, resulting in 24. This demonstrates the inverse relationship between multiplication and division.
-
Problems with Decimals: If the question were "24 times what equals 4.8," we'd simply divide 4.8 by 24, resulting in 0.2. This highlights the adaptability of the method to decimal numbers.
-
Problems with Larger Numbers: If the equation were "144 times what equals 6?" The solution would involve dividing 6 by 144, which results in 1/24 or approximately 0.0417.
-
Word Problems: Real-world problems often disguise the core mathematical concept. For example, "A baker uses 24 cups of flour to make 4 cakes. How much flour is used per cake?" This word problem essentially poses the same question: 24 times what equals 4? The answer, of course, remains 1/6 cups of flour per cake.
Understanding the Significance of the Solution: 1/6
The answer, 1/6, signifies a fraction – a part of a whole. This highlights the importance of understanding fractions and their representation in decimal form. In the context of the original problem, it represents the portion of 24 needed to reach 4. It's also a reminder that mathematical solutions often involve fractions, emphasizing the need to master this fundamental concept.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator to solve this problem? A: Absolutely! Calculators are efficient tools for performing the division operation. However, understanding the underlying mathematical principles is crucial.
-
Q: What if the numbers were different? A: The same method applies. Regardless of the numbers involved, you would always divide the result by the given multiplier to find the unknown.
-
Q: Is there a shortcut method for solving this kind of problem? A: While direct division is often the quickest approach, using proportions or fractional simplification can be equally efficient depending on the numbers involved.
-
Q: Why is it important to learn about division and proportions? A: These fundamental mathematical concepts are crucial for countless applications across various disciplines and in everyday life, making them essential skills to develop.
Conclusion: A Deeper Appreciation of Basic Mathematics
The seemingly simple question, "24 times what equals 4," provides a gateway to exploring fundamental mathematical concepts such as division, proportions, and fractions. Understanding how to solve this type of problem efficiently isn't merely about getting the right answer; it's about grasping the underlying principles that apply to countless other situations, both within the mathematical realm and in our daily lives. This understanding builds a stronger foundation in mathematics, improving problem-solving skills and enriching our ability to navigate a world filled with numerical challenges and opportunities. From baking a cake to analyzing scientific data, the ability to manipulate proportions and understand division proves invaluable. Mastering these concepts allows us to approach challenges with greater confidence and precision.
Latest Posts
Latest Posts
-
1 1000 As A Decimal
Sep 24, 2025
-
4 875 On A Tape Measure
Sep 24, 2025
-
What Are The Factors 60
Sep 24, 2025
-
What Is 60 Of 28
Sep 24, 2025
-
Gcf Of 72 And 36
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 24 Times What Equals 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.