3 1/6 As A Fraction
horsecheck
Sep 25, 2025 · 5 min read
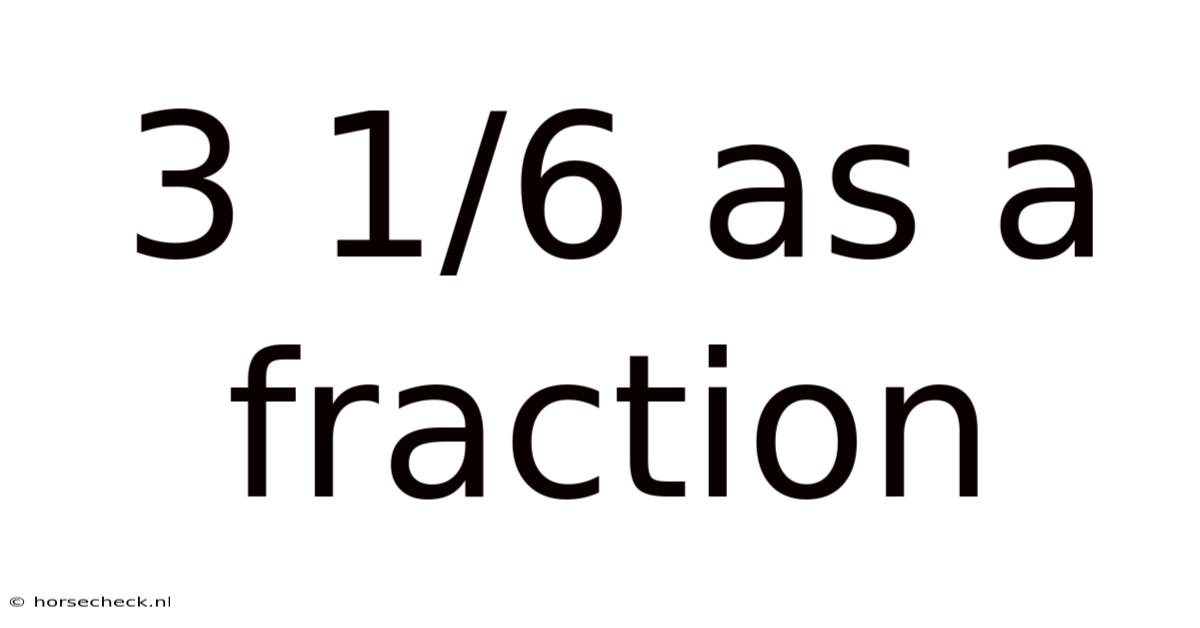
Table of Contents
Understanding 3 1/6 as a Fraction: A Comprehensive Guide
This article delves into the intricacies of the mixed number 3 1/6, explaining its conversion to an improper fraction and exploring the underlying mathematical concepts. We'll cover the steps involved, provide practical examples, and address frequently asked questions to ensure a thorough understanding for learners of all levels. Understanding mixed numbers and improper fractions is crucial for mastering arithmetic and algebra. This guide provides a clear and concise explanation, perfect for students, teachers, and anyone looking to brush up on their fraction skills.
Introduction to Mixed Numbers and Improper Fractions
Before we dive into the specifics of 3 1/6, let's clarify the terminology. A mixed number combines a whole number and a proper fraction. For instance, 3 1/6 represents three whole units and one-sixth of another unit. An improper fraction, on the other hand, has a numerator (the top number) that is greater than or equal to its denominator (the bottom number). Improper fractions represent a value greater than or equal to one. Converting between mixed numbers and improper fractions is a fundamental skill in mathematics.
Converting 3 1/6 to an Improper Fraction: A Step-by-Step Guide
The process of converting a mixed number like 3 1/6 to an improper fraction involves two simple steps:
Step 1: Multiply the whole number by the denominator.
In our example, the whole number is 3, and the denominator of the fraction is 6. Multiplying these together gives us 3 * 6 = 18.
Step 2: Add the numerator to the result from Step 1.
The numerator of our fraction is 1. Adding this to the result from Step 1 (18), we get 18 + 1 = 19.
Step 3: Keep the denominator the same.
The denominator of the original fraction remains unchanged. Therefore, the denominator of our improper fraction is 6.
Step 4: Write the improper fraction.
Combining the results from Steps 2 and 3, we get the improper fraction 19/6. Therefore, 3 1/6 is equivalent to 19/6.
Visual Representation of 3 1/6
Imagine you have three whole pizzas and one-sixth of another pizza. To represent this as an improper fraction, you would need to divide each whole pizza into six equal slices. You would then have 18 slices (3 pizzas x 6 slices/pizza) plus one additional slice, resulting in a total of 19 slices. Since each pizza is divided into six slices, the denominator remains 6. This gives us the improper fraction 19/6.
Why Convert Mixed Numbers to Improper Fractions?
Converting mixed numbers to improper fractions is essential for various mathematical operations, particularly when:
-
Adding or Subtracting Fractions: It's much easier to add or subtract fractions when they share a common denominator. Converting mixed numbers to improper fractions allows for easier standardization.
-
Multiplying or Dividing Fractions: Multiplying and dividing fractions involving mixed numbers are often simplified by first converting the mixed numbers to improper fractions.
-
Solving Algebraic Equations: Many algebraic equations involve fractions, and converting mixed numbers to improper fractions streamlines the solution process.
Further Examples of Mixed Number to Improper Fraction Conversion
Let's practice with a few more examples:
-
2 2/5: (2 * 5) + 2 = 12. The improper fraction is 12/5.
-
1 3/4: (1 * 4) + 3 = 7. The improper fraction is 7/4.
-
5 1/3: (5 * 3) + 1 = 16. The improper fraction is 16/3.
-
10 2/7: (10 * 7) + 2 = 72. The improper fraction is 72/7.
Converting Improper Fractions back to Mixed Numbers
The reverse process is equally important. To convert an improper fraction back to a mixed number, you divide the numerator by the denominator. The quotient becomes the whole number, the remainder becomes the numerator, and the denominator stays the same.
For example, to convert 19/6 back to a mixed number:
19 ÷ 6 = 3 with a remainder of 1. Therefore, 19/6 = 3 1/6.
The Significance of Understanding Fractions
A strong grasp of fractions is fundamental to success in mathematics and related fields. Fractions form the basis for many advanced mathematical concepts, including:
-
Algebra: Fractions are prevalent in algebraic equations and expressions.
-
Calculus: Calculus builds upon the foundational understanding of limits and derivatives, which often involve fractional components.
-
Geometry: Fractional relationships are essential in geometric calculations involving ratios and proportions.
-
Real-world Applications: Fractions are ubiquitous in everyday life, from cooking and baking to budgeting and construction.
Frequently Asked Questions (FAQ)
Q1: Why is it important to learn about improper fractions?
A1: Improper fractions are essential for performing various arithmetic operations smoothly and efficiently, especially when dealing with addition, subtraction, multiplication, and division of fractions and mixed numbers. They provide a standardized format for calculations.
Q2: Can I directly add or subtract mixed numbers without converting them to improper fractions?
A2: While possible, it's generally more complex and prone to errors. Converting to improper fractions first simplifies the process considerably.
Q3: What if I get a remainder of 0 when converting an improper fraction to a mixed number?
A3: If the remainder is 0, the improper fraction is a whole number. For example, 12/3 = 4.
Q4: Are there any shortcuts for converting mixed numbers to improper fractions?
A4: While the step-by-step method is recommended for understanding, a mental shortcut involves multiplying the whole number by the denominator and then adding the numerator. The denominator stays the same.
Conclusion
Understanding how to convert mixed numbers, such as 3 1/6, into improper fractions is a crucial skill in mathematics. This process simplifies many arithmetic operations and forms a foundation for more advanced mathematical concepts. By mastering this skill, you build a solid base for future mathematical endeavors and improve your problem-solving abilities in various contexts. Remember the simple steps: multiply, add, and keep the denominator. Practice makes perfect, so keep working through examples until you feel confident in your ability to convert mixed numbers to improper fractions and vice versa. This skill will serve you well throughout your mathematical journey.
Latest Posts
Latest Posts
-
Gcf For 30 And 18
Sep 25, 2025
-
What Is 80 Of 23
Sep 25, 2025
-
All Factor Pairs Of 24
Sep 25, 2025
-
What Is 1600 Square Root
Sep 25, 2025
-
45 45 45
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 3 1/6 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.