What Is 80 Of 23
horsecheck
Sep 25, 2025 · 5 min read
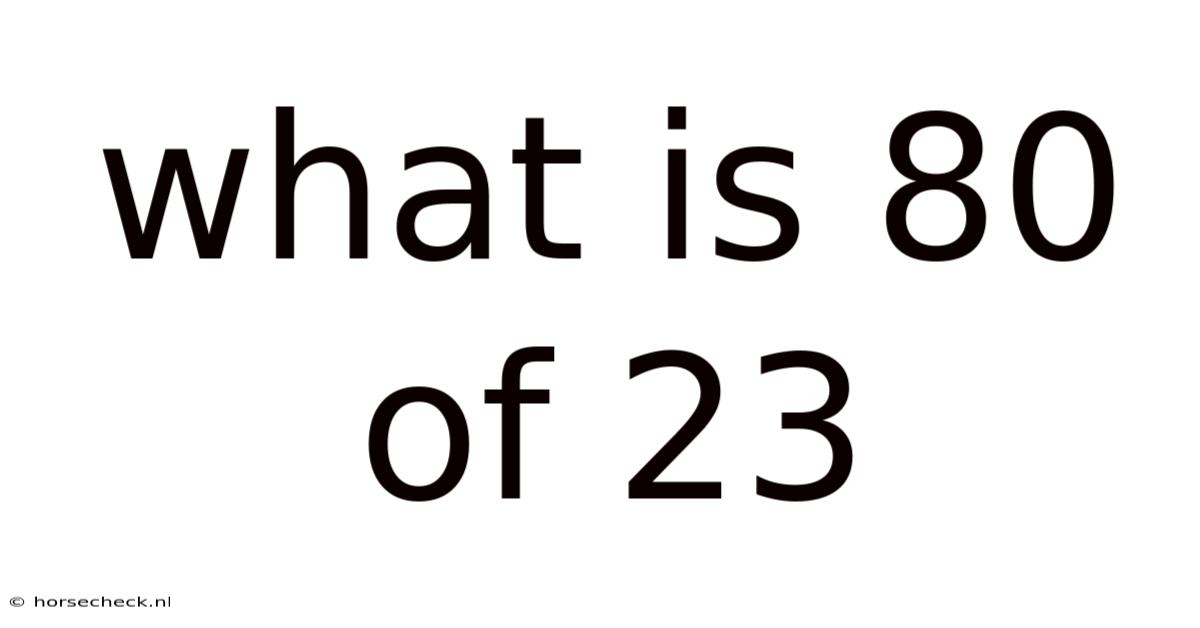
Table of Contents
What is 80% of 23? A Comprehensive Guide to Percentages and Calculations
Finding 80% of 23 might seem like a simple calculation, but it opens the door to understanding a fundamental mathematical concept: percentages. This seemingly straightforward question allows us to explore different methods for calculating percentages, delve into the underlying principles, and even touch upon the practical applications of percentages in everyday life. This comprehensive guide will not only answer the question "What is 80% of 23?" but also equip you with the tools and understanding to tackle similar percentage problems with confidence.
Understanding Percentages: A Foundation for Calculation
Before diving into the calculation itself, let's solidify our understanding of percentages. A percentage is simply a fraction where the denominator is 100. For example, 80% can be written as 80/100, which simplifies to 4/5. This means that 80% represents 80 parts out of a total of 100 parts. Understanding this fundamental concept is crucial for calculating percentages accurately.
Method 1: The Decimal Method – A Straightforward Approach
This is arguably the most straightforward method for calculating percentages. It involves converting the percentage to a decimal and then multiplying it by the number.
-
Step 1: Convert the percentage to a decimal. To convert 80% to a decimal, we divide 80 by 100: 80 ÷ 100 = 0.8
-
Step 2: Multiply the decimal by the number. Now, we multiply the decimal (0.8) by the number we want to find the percentage of (23): 0.8 x 23 = 18.4
Therefore, 80% of 23 is 18.4.
Method 2: The Fraction Method – A Deeper Understanding
This method utilizes the fractional representation of percentages. It offers a deeper understanding of the underlying mathematical principles.
-
Step 1: Convert the percentage to a fraction. As mentioned earlier, 80% can be written as 80/100, which simplifies to 4/5.
-
Step 2: Multiply the fraction by the number. We multiply the simplified fraction (4/5) by 23: (4/5) x 23 = 92/5
-
Step 3: Convert the improper fraction to a decimal. To obtain a decimal value, we divide the numerator (92) by the denominator (5): 92 ÷ 5 = 18.4
Again, we find that 80% of 23 is 18.4.
Method 3: Using Proportions – A Powerful Problem-Solving Technique
The proportion method provides a powerful and versatile approach to solving percentage problems. It relies on setting up a proportion and solving for the unknown value.
-
Step 1: Set up a proportion. We can set up a proportion as follows:
80/100 = x/23
Where 'x' represents the value we want to find (80% of 23).
-
Step 2: Cross-multiply. Cross-multiplying gives us:
100x = 80 * 23
100x = 1840
-
Step 3: Solve for x. Dividing both sides by 100, we get:
x = 1840 ÷ 100 = 18.4
Once more, we arrive at the answer: 80% of 23 is 18.4.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is crucial in numerous real-world scenarios. Here are a few examples:
-
Sales and Discounts: Calculating discounts in stores, online shopping, and sales. For instance, if a product is discounted by 20%, you would use percentage calculations to determine the final price.
-
Finance and Investments: Determining interest rates, calculating returns on investments, understanding loan payments, and analyzing financial statements all rely heavily on percentages.
-
Statistics and Data Analysis: Percentages are used extensively in presenting and interpreting data, expressing probabilities, and understanding proportions within a dataset.
-
Science and Engineering: Percentages are used to express concentrations, efficiencies, and error margins in various scientific and engineering fields.
-
Everyday Life: From calculating tips in restaurants to understanding tax rates and determining the percentage of ingredients in a recipe, percentages are embedded in our daily lives.
Beyond the Basics: Working with Different Percentages
The methods described above can be easily adapted to calculate any percentage of any number. Simply replace the 80% and 23 with the desired percentage and number. For example, to find 35% of 60:
- Decimal Method: 0.35 x 60 = 21
- Fraction Method: (35/100) x 60 = (7/20) x 60 = 21
- Proportion Method: 35/100 = x/60; 100x = 2100; x = 21
Frequently Asked Questions (FAQ)
Q: What if the percentage is less than 1%?
A: The same methods apply. For instance, to find 0.5% of 23, you would convert 0.5% to a decimal (0.005) and multiply by 23: 0.005 x 23 = 0.115
Q: How do I calculate a percentage increase or decrease?
A: Percentage increase/decrease calculations require a slightly different approach. To calculate a percentage increase, find the difference between the new and original values, divide the difference by the original value, and multiply by 100. Percentage decrease is calculated similarly.
Q: Can I use a calculator for percentage calculations?
A: Yes, most calculators have a percentage function (%) that simplifies the calculation. However, understanding the underlying methods is crucial for solving problems even without a calculator.
Q: Are there online calculators for percentages?
A: Yes, many websites offer online percentage calculators that can quickly compute percentages for various inputs. However, it’s beneficial to understand the fundamental calculations to apply them effectively across varied situations.
Conclusion: Mastering Percentage Calculations
Calculating 80% of 23, as demonstrated, is a simple yet powerful illustration of percentage calculations. By understanding the different methods—the decimal method, the fraction method, and the proportion method—you gain a deeper comprehension of percentages and their applications. This knowledge extends far beyond simple calculations; it’s a fundamental skill valuable in various aspects of life, from managing personal finances to interpreting data and solving complex problems. Practice these methods regularly to solidify your understanding and build confidence in tackling percentage-related challenges with ease. Remember, the key to mastering percentages lies not just in memorizing formulas but in truly grasping the underlying mathematical concepts.
Latest Posts
Latest Posts
-
8 Out Of 25 Percentage
Sep 25, 2025
-
18 Out Of 28 Percentage
Sep 25, 2025
-
Gcf Of 40 And 28
Sep 25, 2025
-
Numbers That Have 3 Factors
Sep 25, 2025
-
1 6 Equals What Percent
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of 23 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.