3.75 As A Mixed Fraction
horsecheck
Sep 25, 2025 · 6 min read
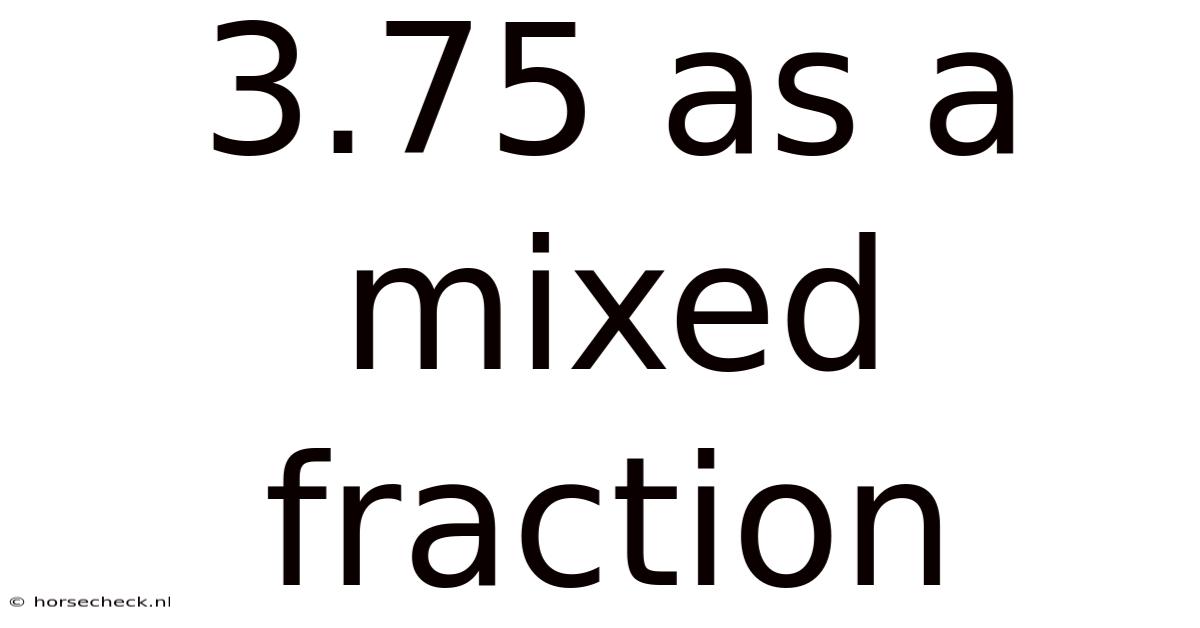
Table of Contents
Understanding 3.75 as a Mixed Fraction: A Comprehensive Guide
Understanding decimal numbers and their fractional equivalents is a fundamental skill in mathematics. This article delves deep into converting the decimal 3.75 into a mixed fraction, explaining the process step-by-step and providing a solid understanding of the underlying concepts. We'll explore the definition of mixed fractions, the conversion process, and even tackle some related frequently asked questions. This guide is designed for learners of all levels, from those just grasping the basics to those seeking a more thorough understanding.
What is a Mixed Fraction?
Before we dive into converting 3.75, let's clarify what a mixed fraction is. A mixed fraction is a combination of a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 1 ¾, 2 ⅓, and 5 ²/₅ are all mixed fractions. They represent a quantity that is greater than one whole unit.
Converting 3.75 to a Mixed Fraction: A Step-by-Step Guide
The conversion of 3.75 to a mixed fraction involves several key steps. Let's break down the process clearly:
Step 1: Identify the Whole Number Part
The decimal 3.75 clearly shows a whole number part of 3. This will be the whole number component of our mixed fraction.
Step 2: Convert the Decimal Part to a Fraction
The decimal part of 3.75 is 0.75. To convert this to a fraction, we consider the place value of the last digit. The '5' is in the hundredths place, meaning it represents 75/100. So, 0.75 is equivalent to the fraction ⁷⁵⁄₁₀₀.
Step 3: Simplify the Fraction
The fraction ⁷⁵⁄₁₀₀ can be simplified by finding the greatest common divisor (GCD) of the numerator (75) and the denominator (100). The GCD of 75 and 100 is 25. Dividing both the numerator and the denominator by 25, we get:
⁷⁵ ÷ 25 = 3 ₁₀₀ ÷ 25 = 4
This simplifies our fraction to ³⁄₄.
Step 4: Combine the Whole Number and the Simplified Fraction
Now, we combine the whole number part (3) from Step 1 with the simplified fraction (³/₄) from Step 3. This gives us our final mixed fraction: 3 ¾.
Therefore, 3.75 expressed as a mixed fraction is 3 ¾.
Deeper Dive: Understanding the Conversion Process
The conversion process we just completed relies on the fundamental principle of representing decimal numbers as fractions. Decimal numbers are based on powers of 10. For example:
- 0.1 = 1/10 (one-tenth)
- 0.01 = 1/100 (one-hundredth)
- 0.001 = 1/1000 (one-thousandth) and so on.
When we have a decimal like 0.75, we can break it down:
0.75 = 0.7 + 0.05 = (7/10) + (5/100)
To add these fractions, we need a common denominator, which is 100 in this case. So we convert 7/10 to 70/100:
(70/100) + (5/100) = 75/100
This is precisely the fraction we obtained in Step 2 of our conversion. Simplifying this fraction further, as we did, leads us to the simplest form, ³⁄₄. This understanding highlights the interconnectedness between decimals and fractions.
Practical Applications of Mixed Fractions
Mixed fractions are frequently used in various real-world scenarios. Consider these examples:
- Measurement: Measuring ingredients in a recipe often involves mixed fractions (e.g., 2 ½ cups of flour).
- Construction: Construction projects use mixed fractions for dimensions and measurements.
- Everyday life: Sharing items equally, such as cutting a cake into portions, often results in mixed fractions.
Understanding how to convert decimals to mixed fractions is crucial for effectively handling these situations and solving problems involving measurements and quantities.
Converting Other Decimals to Mixed Fractions
Let's apply the same principles to convert other decimal numbers into mixed fractions:
Example 1: 2.25
- Whole number: 2
- Decimal part: 0.25 = 25/100
- Simplification: 25/100 = ¼ (dividing by 25)
- Mixed fraction: 2 ¼
Example 2: 5.6
- Whole number: 5
- Decimal part: 0.6 = 6/10
- Simplification: 6/10 = ³⁄₅ (dividing by 2)
- Mixed fraction: 5 ³⁄₅
Example 3: 1.125
- Whole number: 1
- Decimal part: 0.125 = 125/1000
- Simplification: 125/1000 = ⅛ (dividing by 125)
- Mixed fraction: 1 ⅛
Converting Improper Fractions to Mixed Numbers
It's also important to note the relationship between improper fractions and mixed numbers. An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 7/4). To convert an improper fraction to a mixed number, you divide the numerator by the denominator. The quotient becomes the whole number part, and the remainder becomes the numerator of the fractional part, with the denominator remaining the same.
For instance, to convert 7/4 to a mixed number:
7 ÷ 4 = 1 with a remainder of 3.
Therefore, 7/4 = 1 ¾. This process is the reverse of converting a mixed number to an improper fraction.
Frequently Asked Questions (FAQ)
Q1: Why is it important to simplify fractions?
Simplifying fractions makes them easier to work with and understand. A simplified fraction represents the same value as the original fraction but in its most concise form.
Q2: What if the decimal has more than two decimal places?
The process remains the same. You identify the whole number part, convert the decimal part to a fraction based on its place value (e.g., thousandths, ten-thousandths), and then simplify the resulting fraction.
Q3: Can all decimals be converted to mixed fractions?
Yes, all terminating decimals (decimals that end) can be converted to mixed fractions or proper fractions. Repeating decimals (decimals that continue infinitely with a repeating pattern) can also be converted to fractions, but the process is slightly more complex and involves algebraic manipulation.
Q4: What is the difference between a mixed fraction and an improper fraction?
A mixed fraction combines a whole number and a proper fraction, while an improper fraction has a numerator greater than or equal to its denominator.
Q5: How can I check if my conversion is correct?
You can convert the mixed fraction back to a decimal to verify your answer. For example, to check if 3 ¾ is equal to 3.75, convert ¾ to a decimal by dividing 3 by 4 (3 ÷ 4 = 0.75), then add the whole number 3 (3 + 0.75 = 3.75).
Conclusion
Converting decimals to mixed fractions is a fundamental mathematical skill with broad applications. By understanding the step-by-step process and the underlying principles, you can confidently tackle this type of conversion and apply it to various real-world problems. Remember to always simplify your fractions to their simplest form for clarity and ease of use. This comprehensive guide provides a solid foundation for mastering this essential concept. Through practice and understanding the logic behind the conversions, you'll become increasingly proficient in working with decimals and fractions.
Latest Posts
Latest Posts
-
2 To Power Of 3
Sep 25, 2025
-
Whats 75 Percent Of 50
Sep 25, 2025
-
12 To The 12th Power
Sep 25, 2025
-
1600 Degrees Celsius To Fahrenheit
Sep 25, 2025
-
Gcf Of 20 And 12
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 3.75 As A Mixed Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.